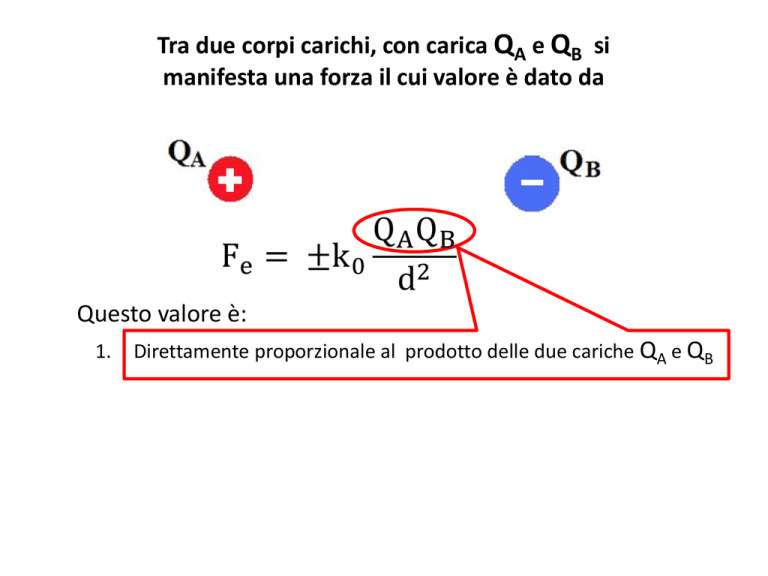
Tra due corpi carichi, con carica QA e QB si
manifesta una forza il cui valore è dato da
Questo valore è:
1.
Direttamente proporzionale al prodotto delle due cariche QA e QB
Tra due corpi carichi, con carica QA e QB si
manifesta una forza il cui valore è dato da
d
Questo valore è:
1.
Direttamente proporzionale al prodotto delle due cariche QA e QB
2.
Inversamente proporzionale al quadrato della loro distanza reciproca d
Tra due corpi carichi, con carica QA e QB si
manifesta una forza il cui valore è dato da
d
Questo valore è:
1.
Direttamente proporzionale al prodotto delle due cariche QA e QB
2.
Inversamente proporzionale al quadrato della loro distanza reciproca d
Tra due corpi carichi, con carica QA e QB si
manifesta una forza il cui valore è dato da
d
Ko si chiama costante elettrica del vuoto o costante di Coulomb
Forza (interazione) elettrostatica o di Coulomb
Se le cariche sono di segno opposto la forza di
Coulomb è attrattiva
Se le cariche sono di segno opposto la forza di
Coulomb è attrattiva
Se le cariche sono di segno opposto la forza di
Coulomb è attrattiva
Questo vettore rappresenta la
forza elettrostatica dovuta a
QB che agisce sulla carica QA
Questo vettore rappresenta la
forza elettrostatica dovuta a
QA che agisce sulla carica QB
Le due forze sono uguali e opposte
Se le cariche hanno lo stesso segno la forza di
Coulomb è repulsiva
Se le cariche hanno lo stesso segno la forza di
Coulomb è repulsiva
Se riportiamo in un sistema di assi cartesiani la forza in funzione della distanza
reciproca tra le due cariche F
= F(d) si ottiene il grafico seguente
Se riportiamo in un sistema di assi cartesiani la forza in funzione della distanza
reciproca tra le due cariche F
= F(d) si ottiene il grafico seguente
Matematicamente è un grafico del
tipo
L’unità di misura della carica elettrica, nel SI, è il Coulomb
che si definisce a partire dall’Ampere, unità di misura
dell’Intensità di Corrente elettrica
Questo modo di procedere discende dal fatto che nel SI la
grandezza fisica fondamentale per la descrizione dei
fenomeni elettromagnetici è l’Intensità di Corrente e non la
Carica Elettrica.
Ma è necessario, almeno provvisoriamente, dare una definizione
del Coulomb
Questo si può fare partendo dalla legge che descrive
l’interazione elettrostatica
Consideriamo:
QA = QB = 1C
K0 = 9x109 Nm2/C2
d = 1m
1
!!!!!!
È una forza enorme!!!!!!
Significa che due corpi carichi con 1C ciascuno si attraggono o
si respingono con una forza di 9 MILIARDI (109) di Newton
9 MILIARDI (109) di Newton corrispondono, ad esempio, alla
forza peso di 900 milioni di chili (108 kg)
Questo significa che la carica elettrica di 1C è enorme
Di conseguenza si utilizzano i sottomultipli
10-3 C = mC (milli Coulomb)
10-6 C = mC (micro Coulomb)
10-9 C = nC (nano Coulomb)
10-12 C = pC (pico Coulomb)
Quanti elettroni sono necessari per formare la carica di 1C ?
e = 1,602 10-19 C
Un esempio di applicazione della forza elettrostatica
Il caso del legame ionico nel
cloruro di sodio (NaCl)
Nel cloruro di sodio il legame tra lo ione sodio Na+ e lo
ione cloro Cl- può essere descritto come
forza di attrazione tra cariche di segno opposto
Calcolare la forza che nel cloruro di sodio (NaCl) tiene uniti lo
ione cloro e lo ione sodio
Reticolo
cristallino del
cloruro di
sodio
Calcolare la forza che nel cloruro di sodio (NaCl) tiene uniti lo
ione cloro e lo ione sodio
Na+
Cl-
Calcolare la forza che nel cloruro di sodio (NaCl) tiene uniti lo
ione cloro e lo ione sodio
276 pm
Na+
ClDistanza tra i
centri dei due
ioni
Calcolare l’intensità della forza elettrostatica che nel cloruro di
sodio (NaCl) tiene uniti lo ione cloro e lo ione sodio
276 pm
Na+
Cl-
Anche per la forza di Coulomb (interazione elettrostatica) sono
valide le stesse obiezioni fatte per l’interazione gravitazionale:
1. Il tempo non compare esplicitamente nella legge e questo
farebbe supporre che le due cariche elettriche «sentano»
immediatamente la reciproca presenza;
2. La forza coulombiana sembrerebbe agire a distanza ma
l’azione a distanza non è un concetto scientifico; deve quindi
esistere un «mediatore», fisicamente riscontrabile, che fa da
tramite tra le due cariche.
Queste due incongruenze vengono risolte con l’introduzione del
concetto di campo, in questo caso il CAMPO ELETTRICO
Una carica elettrica modifica, con la sua presenza, lo spazio
circostante che diventa uno spazio «fisico»
QA
Il campo Elettrico si forma alla velocità della luce
QA
?
QA
?
QA
QA
?
Il campo gravitazionale plasma la struttura dello spazio
ANZI
IL CAMPO GRAVITAZIONALE E’ LO SPAZIO-TEMPO
Il campo elettrico e più in generale il campo elettromagnetico si
conformano alla struttura dello spazio-tempo della teoria della
relatività generale
Le onde elettromagnetiche si propagano seguendo le
deformazioni dello spazio-tempo
Le onde elettromagnetiche si propagano seguendo le
deformazioni dello spazio-tempo
Percorso di un «raggio di luce» ( fotoni oppure onda
elettromagnetica a seconda del tipo di descrizione) in
uno spazio-tempo non deformato
Percorso di un «raggio di luce» ( fotoni oppure onda
elettromagnetica a seconda del tipo di descrizione) in
uno spazio-tempo deformato
La carica QA è immersa nel campo elettrico da essa stessa creato.
QA
Consideriamo un punto qualunque P nello spazio attorno alla carica QA o
come è meglio dire, un punto del campo elettrico creato da QA.
P
QA
Consideriamo un punto qualunque P del campo elettrico creato da QA.
P
QA
Se nel punto P
mettiamo una carica QB positiva
QB
QA
QB
QA
Se mettiamo la carica QB in un altro punto del
campo
QB
QA
Se cambiamo ancora punto
QA
QB
E’ come se le cariche che via via si venissero a trovare nel campo elettrico creato dalla carica
QA seguissero delle traiettorie prestabilite.
Queste traiettorie vengono chiamate linee di forza del campo elettrico.
In questo caso le linee di forza sono delle rette a direzione radiale e il
campo è a simmetria sferica con il centro costituito dalla carica che crea il
campo
Le linee di forza sono delle rette a direzione radiale e il campo è a
simmetria sferica con il centro costituito dalla carica che crea il campo
Linee di forza
QB
P
QA
QBC
P
QA
Mettiamo una carica diversa nel
punto P
La carica
QC
QCD
P
QA
Cambiamo ancora la carica nel
punto P
Mettiamo la carica
QD
QND
P
Possiamo cambiare la carica nel
punto P infinite volte
Mettiamo la carica
QN
QA
Riepiloghiamo
QN
P
d(P)
QA
. . . . .
Riepiloghiamo
QN
P
d(P)
QA
Cosa possiamo notare?
. . . . .
Cosa possiamo notare?
QN
P
Che nel punto P può
esserci una carica Q
qualsiasi
d(P)
QA
. . . . .
dipende
dalla carica QA che crea il campo
dalla distanza d del punto P
e da k0
Non dipende in alcun modo dalla
carica QN che di volta in volta
potrebbe trovarsi nel punto P
. . . . .
può essere utilizzata per descrivere il campo elettrico nel
punto P e in tutti i punti del campo che, come P, si trovano
alla distanza d
perchè Il campo elettrico è a simmetria sferica o
radiale
Consideriamo
Dividiamo I e II membro per
QN e semplifichiamo
otteniamo
Rappresenta il valore del
campo elettrico alla
distanza d
Essendo il rapporto tra una forza, quella elettrostatica, e una
carica elettrica, l’unità di misura del campo elettrico è il N/C
(Newton/Coulomb)
Il campo elettrico ha lo stesso valore in tutti i punti che hanno la
stessa distanza dalla carica che lo crea.
La carica Q genera un campo elettrico a simmetria sferica
Tracciare i vettori che lo rappresentano nei punti A e B
Q
B
A












