Corrente Elettrica
Finora abbiamo considerato le cariche elettriche fisse: Elettrostatica
Consideriamole adesso in movimento !
La carica in moto forma una corrente elettrica.
L’intensità di corrente è uguale al “tasso” (rapidità) con cui le
cariche si muovono attraverso una ipotetica sezione di un
conduttore
dq
i
dt
• La direzione della corrente è definita come la direzione in
cui si muovono le particelle cariche positivamente.
Comunue, la corrente è uno scalare.
Q
Q n V q n A xl q n A vd t q I
n q vd A
t
Fisica II - Informatica
Corrente Stazionaria (o continua)
Una corrente elettrica la cui intensità non varia nel tempo.
Una volta raggiunto lo stato stazionario, la corrente è la stessa
attraverso una qualunque sezione di un conduttore (continuità).
La carica totale che passa attraverso una sezione in un intervallo di
tempo t è data da
t
q dq idt it
0
Unità SI : Ampere (A)
1 A = 1 C/s
Fisica II - Informatica
Densità di Corrente
• La densità di corrente è un vettore.
• La direzione della densità di
corrente in un dato punto è la
direzione in cui si muove una
carica positiva.
• L’intensità della densità di corrente
è tale che la corrente totale
attraverso una sezione è data da
Linee di flusso del
campo di corrente
i J dA
se la corrente èuniforme e parallela a dA
i J dA J dA JA
Fisica II - Informatica
J i A
Aspetti Microscopici
• Quanti elettroni mobili che ci sono in un conduttore ?
Esempio – Il rame è utilizzato comunemente nell’impianto
elettrico delle abitazioni. Quanti sono gli elettroni mobili che
troviamo in un filo di rame ?
La densità del rame è 8.95 g/cm3 ed il suo peso molecolare 63.5
g/mole (in una mole di qualunque sostanza contiene un numero
di atomi pari al numero di Avogadro 6.021023 atomi.
Nell’ipotesi che vi sia un solo elettrone mobile per ciascun un
atomo di rame:
m
63.5 g
3
V
7.09
cm
8.95 g cm3
N Av 6.02 1023 elettroni
22 elettroni
28 elettroni
n
8.49 10
8.49 10
3
3
V
7.09 cm
cm
m3
Fisica II - Informatica
Aspetti Microscopici
• Le cariche mobili, cioè gli elettroni, si trovano nei
conduttori con una densità, ne (ne 1029 m-3)
• Il campo elettrico E mette in moto
gli elettroni:
– tutte le cariche si muovono con una
velocità, ve
– “gran parte” del moto è di tipo
“casuale” (in tutte le direzioni on
media nulla) con una piccola velocità
media eguale a vd
velocità di deriva
La velocità dovuta al moto casuale è
dell’ordine di 106 m/s. Mentre, la velocità
di deriva è solo 10 -5 m/s.
Fisica II - Informatica
Aspetti Microscopici
• Densità di Corrente, J, è data da J = qenevd
– unità di J è C/m2sec ovvero Ampere/m2
– la corrente, I, è J moltiplicato l’area della sezione,
p.es. I = J pr2 se circolare.
• Il campo E in un conduttore è generato da una batteria
• Le cariche sono messe in movimento, ma vengono
“diffuse” in tempi molto brevi da “oggetti” sul loro
cammino
– c’è un grande “affollamento” all’interno del metallo
– difetti, vibrazioni reticolari, ecc.
• Tipico tempo di “diffusione” t = 10-14 sec
• le cariche sono accelerate durante questo tempo e,
successivamente, diffuse casualmente
Fisica II - Informatica
Aspetti Microscopici
• A che velocità si muovono gli elettroni mobili ?
Esempio – Un filo di rame ha diametro di 2.5 mm2 e sezione di
circa 5 mm2, se è attraversato da una corrente di 10 A a che
velocità media si muovono gli elettroni ?
Noto il numero di elettroni liberi nel rame (vedi es. precedente),
la velocità di deriva vale:
J
I
vd
ne neA
10 C s
4 m
1.46 10
elettroni
s
19
6
2
8.49 1028
1.6
10
C
5
10
m
m3
Non sembra particolarmente elevata: ci vogliono circa 15000
sec per percorrere 1 metro (4 ore !!!).
Fisica II - Informatica
Aspetti Microscopici
• la velocità media raggiunta in questo F ma v eEt
d
tempo è [ eE=forza, forza/m = a, v=at ]
m
• la densità di corrente è J = nevd , quindi la corrente è
proporzionale ad E che è proporzionale alla d.d.p.
I J v E V V I R
V
1V
R
resistenza unità di misura ohm , 1
I
1A
• In diversi casi R=cost al variare di V
Legge di OHM
Legge di OHM non è una legge fondamentale della natura !
Piuttosto è una relazione empirica valida soltanto per certi
materiali e/o dispositivi, in un campo limitato di condizioni !
p.es. i semiconduttori, ed i dispositivi (diodo, transistor) sono
non-ohmici
Fisica II - Informatica
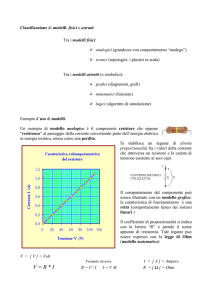
Validità della legge di Ohm
Un materiale conduttore obbedisce alla legge di Ohm
quando la resistività del materiale è indipendente
dall’intensità e direzione del campo elettrico applicato.
ohmico
non-ohmico
Comunque, la resistività è, in generale, dipendente dalla
temperatura. La dipendenza è all’incirca lineare (per i metalli), i.e.
0 0 T T0
coefficiente di temperatura
della resistività,
I metalli obbediscono alla legge di Ohm solo quando la
temperatura è mantenuta costante durante la misura.
Fisica II - Informatica
Resistività e coefficienti termici della
resistività per alcuni materiali:
Fisica II - Informatica
Aspetti Microscopici
(definizioni)
Sulla base delle relazioni precedenti possiamo riscrivere la
legge di OHM in forma microscopica (prescindendo dalla
forma e dimensioni del conduttore):
ne2t
J
m
Conducibilità
ne t
m
2
Fisica II - Informatica
E ovvero J E
Resistività
1
E J
R
I
Resistenza
I
V
•Resistenza
La resistenza è definita come il
rapporto tra la d.d.p. applicata
e la corrente che la attraversa.
V
R
I
Unità: OHM =
Effetto delle dimensioni
R
L
A
E
j
A
L
• All’aumentare della lunghezza, il flusso di elettroni è limitato
• All’aumentare dell’area della sezione il flusso è favorito
• Analogia (macroscopica) con il flusso di acqua in una conduttura
Fisica II - Informatica
Aspetti Macroscopici
• Le proprietà di un materiale dipendono
dalle sue proprietà microscopiche
Se il materiale è uniforme:
j
I
A
V EL
E
j
A
L
I
ρL
V EL jL
L I
A
A
Fisica II - Informatica
V IR
L
con R
A
Legge di Ohm
(R=cost.)
Aspetti Macroscopici (riassumendo ...)
V IR
con
L
R
A
E
j
A
L
Legge di Ohm:
è indipendente dalla forma del resistore.
La formula per R NON E’ la legge di Ohm, ed è
valida per conduttori di sezione arbitraria,
MA SOLO SE la sezione è la stessa per tutta la
lunghezza.
Fisica II - Informatica
Esempio #1
Due resistori cilindrici sono realizzati con
lo stesso materiale, e sono di lunghezza
eguale. Il primo resistore ha diametro d,
ed il secondo resistore ha diametro 2d.
Confrontare la resistenza dei due cilindri.
a) R1 > R2
Fisica II - Informatica
b) R1 = R2
c) R1 < R2
Esempio #2
Due resistori cilindrici sono realizzati con
lo stesso materiale, e sono di lunghezza
eguale. Il primo resistore ha diametro d,
ed il secondo resistore ha diametro 2d.
Se la stessa corrente fluisce attraverso entrambi i resistori, confrontare
le velocità di deriva medie degli elettroni nei due resistori:
a) v1 > v2
Fisica II - Informatica
b) v1 = v2
c) v1 < v2
Superconduttori
Per una classe di metalli e composti noti come
superconduttori la resistenza diventa zero al di
sotto di una particolare temperatura critica Tc.
Levitazione di un magnete permanente su un
disco superconduttore alla temperatura dell’azoto
liquido -196 ºC (77 K).
Fisica II - Informatica
Energia e Potenza nei circuiti elettrici
V
Supponiamo che la corrente nel circuito
in fig. sia i, fluendo attraverso la d.d.p. V.
In un intervallo di tempo dt, la quantità di
carica che si muove da a a b è quindi
dq = idt. La variazione nell’energia
potenziale associata con questa carica è
dU dq V idt V
Rammentiamo:
Potenza = (Energia)/(intervallo di Tempo)
Pertanto, la potenza associata
con il trasferimento di carica è
Per un dispositivo di resistenza R,
la dissipazione di potenza è
Fisica II - Informatica
dU
P
iV
dt
Tre modi per
scrivere P.
2
V
Pi R
R
2
Generatore di forza
elettromotrice f.e.m.
Un dispositivo che mantiene una differenza di potenziale
tra una coppia di terminali
• batterie
• generatori elettrici
• celle solari
• termopile
• celle a combustibile
L’energia si conserva ! Un dispositivo f.e.m. converte
semplicemente altre forme di energia (p.es., chimica,
meccanica, solare, termica, e così via) in energia elettrica.
Fisica II - Informatica
F.E.M.
Forza Elettromotrice
All’interno di un dispositivo f.e.m., i portatori di carica
positiva si muovono dal terminale a potenziale più
basso (cioè, il terminale negativo) a quello a potenziale
più alto (cioè, il terminale positivo).
Quindi del lavoro deve essere
svolto nel processo. La f.e.m.
del dispositivo è definita come
lavoro per unità di carica:
dW
dq
Fisica II - Informatica
unità SI: volt (V)
1 J/C = 1 V
Dispositivi f.e.m. ideali e reali
• Dispositivo f.e.m. ideale: un dispositivo f.e.m. in cui
i portatori di carica non subiscono alcun effetto di
resistenza elettrica quando si muovono da un
terminale all’altro. In questo caso, la differenza di
potenziale tra i due terminali è eguale alla f.e.m. del
dispositivo.
• Dispositivo f.e.m. reale: un dispositivo f.e.m. in cui i
portatori di carica subiscono un effetto di
resistenza elettrica quando si muovono da un
terminale all’altro. In questo caso, la differenza di
potenziale tra i due terminali è più piccola della
f.e.m. del dispositivo, a causa della dissipazione di
energia interna. Ci riferiamo a questo fenomeno
come caduta di tensione Ohmica.
Fisica II - Informatica
Conservazione dell’energia
Consideriamo un circuito costituito da una batteria ideale (B)
con f.e.m. , un resistore R, e due fili di connessione (con
resistenza trascurabile).
• Conservazione Energia: l’energia dissipata nel resistore
deve eguagliare il lavoro fatto dalla batteria
Durante un intervallo di tempo dt, il lavoro svolto dalla
batteria è dW = dq = i dt, e l’energia dissipata nel
resistore è dE = i2R dt.
Eguagliando le due relazioni si ha i = / R.
Fisica II - Informatica
Generatore di f.e.m. reale
V I r
I RI r
I
poichè V I R
Rr
2
2
Pbatt I I R I r
la resistenza interna del generatore deve
essere trascurabile rispetto a quella del
carico per avere un efficiente
trasferimento di energia !
Fisica II - Informatica
Resistori
in
serie
Consideriamo un circuito costituito da una batteria ideale e
due lampadine con resistenze R1 e R2.
deve essere I cost per cui V Vac Vab Vbc IR1 IR2
quindi V IReq IR1 IR2 Req R1 R2
in generale
Req R1 R2 R3 ...
La resistenza equivalente di un insieme di resistori collegati in
serie è uguale alla somma delle singole resistenze ed è sempre
maggiore di ciascuna di esse
Fisica II - Informatica
Resistori in parallelo
Consideriamo un circuito costituito da una batteria ideale e
due lampadine collegate in parallelo con resistenze R1 e R2.
deve essere V cost
quindi
I I1 I 2
1
1 1
in generale
Req R1 R2
1 1 V
V V
V
R1
R2
R1 R2 Req
1
1 1
1
...
Req R1 R2 R3
L’inverso della resistenza equivalente di due o più resistori
collegati in parallelo è uguale alla somma dell’inverso delle
singole resistenze ed è sempre minore del più piccolo resistore
Fisica II - Informatica
Esempio
1)
2)
3)
4)
Le lampadine collegate al
generatore in questo modo,
sono tutte eguali:
quale sarà, nell’ordine, la loro
luminosità ?
cosa succede se si interrompe
A (“si brucia) ?
se si interrompe C ?
se si interrompe D ?
1. in C e in A+B passa la stessa corrente, quindi C sarà
più luminosa di A o B, che hanno la stessa luminosità; D
non si accenderà mai (ha i terminali in corto-circuito)
2. B si spegne, C più luminosa, D sempre spenta
3. A e B più luminose, D sempre spenta
4. ininfluente
Fisica II - Informatica
Esempio
a) trovare la resistenza equivalente della
rete di resistori in grafico
b) qual è la corrente in ciascun resistore
se la d.d.p. tra a e c vale Vac=42V
Applicando le relazioni
per collegamento in serie
e parallelo di resistenze
Req 14
La corrente nelle resistenze da 8 e 4 è cost usando V IR si ha
V
42V
I ac
3A
Ai capi b e c V cost quindi
Req 14
6 I1 3 I 2 da cui I 2 2 I1 , inoltre I1 I 2 I 3 A I1 1 A e I 2 2 A
Fisica II - Informatica