Circuiti Elettrici
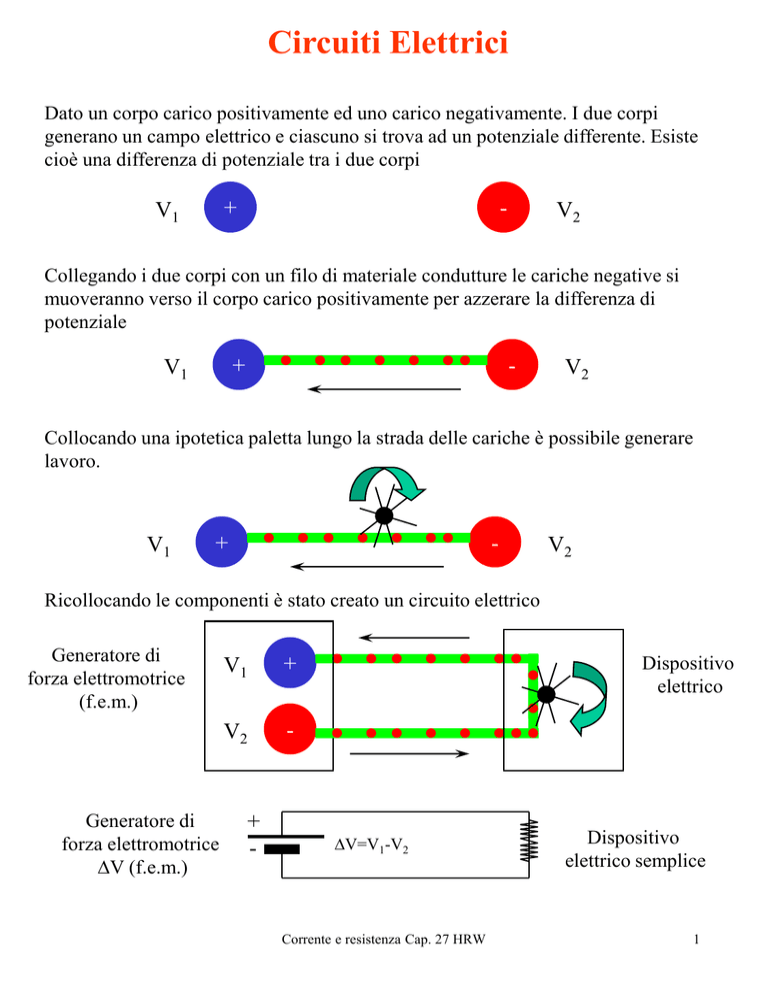
Dato un corpo carico positivamente ed uno carico negativamente. I due corpi
generano un campo elettrico e ciascuno si trova ad un potenziale differente. Esiste
cioè una differenza di potenziale tra i due corpi
+
V1
-
V2
Collegando i due corpi con un filo di materiale condutture le cariche negative si
muoveranno verso il corpo carico positivamente per azzerare la differenza di
potenziale
+
V1
-
V2
Collocando una ipotetica paletta lungo la strada delle cariche è possibile generare
lavoro.
V1
+
-
V2
Ricollocando le componenti è stato creato un circuito elettrico
Generatore di
forza elettromotrice
(f.e.m.)
Generatore di
forza elettromotrice
DV (f.e.m.)
V1
+
V2
-
+
-
Dispositivo
elettrico
DV=V1-V2
Corrente e resistenza Cap. 27 HRW
Dispositivo
elettrico semplice
1
Corrente e resistenza Cap. 27 HRW
2
Generatore
Strumento in grado di mantenere ai suoi capi un differenza di potenziale ΔV
chiamata forza elettromotrice (f.e.m.)
Corrente elettrica
Il movimento ordinato di cariche elettriche è detto corrente elettrica
Intensità di corrente elettrica
L’intensità di corrente elettrica è data dalla quantità di carica dq che passa
nell’intervallo di tempo dt. L’intensità di corrente elettrica si misura in Ampere
I
dq
dt
I C Ampere
s
La corrente elettrica, per convenzione, scorre dal polo positivo al polo negativo (in
verso opposto al reale verso di scorrimento degli elettroni)
Se le cariche si muovono sempre nel medesimo verso la corrente è detta continua, se le
cariche cambiano verso di scorrimento periodicamente la corrente è detta alternata.
Potenza
La potenza dissipata da un circuito in cui scorre una corrente I indotto da una differenza
di potenziale DV costante nel tempo è dato dal prodotto IDV
dL d
d
DU qDV
dt dt
dt
dq
P DV
IDV se DV costante nel tempo
dt
P
Corrente e resistenza Cap. 27 HRW
3
Densità di Corrente
La densità di corrente è definita come il vettore orientato come il vettore
velocità delle cariche in moto, il medesimo verso, se le cariche sono
positive, o opposto se le cariche sono negative e modulo pari alla intensità
di corrente per unità di area.
i J d A
Se i è costante in tutto un conduttore di superficie A :
i
J
A
A
i
Nota:
La densità di corrente è un vettore, l’intensità di corrente i non lo è.
L’unità di misura di J è Ampere/m2
Corrente e resistenza Cap. 27 HRW
4
Velocità di deriva
Ogni secondo, attraverso un conduttore di sezione A percorso da una
corrente I passa un numero di elettroni pari a:
N
N
N
N
(# elettroni per unità di volume) *Volume
(# elettroni per unità di volume) * A * L
(# elettroni per unità di volume) * A * (velocità elett.) * tempo
n * A * vd * t
Cioè una carica pari a :
Q qe * n * A * vd * t
Cioè una corrente pari a :
Q
i qe * n * A * v d
t
La velocità di deriva degli elettroni è quindi:
i
J
vd
nqe A nqe
La velocità di deriva degli elettroni è molto bassa, dell’ordine di 10 -7 m/s
Corrente e resistenza Cap. 27 HRW
5
Legge di Ohm
Sperimentalmente si osserva che, nella grande maggioranza dei conduttori (ma non in
tutti), l’intensità di corrente elettrica dipende linearmente dalla differenza di potenziale
applicata. La costante di proporzionalità si chiama resistenza e dipende dalle proprietà
fisico chimiche (struttura atomica, forma, temperature, … ) del conduttore.
DV RI
l
R
S
R resistenza
R Ohm
S
l lunghezza del conduttore
S sezione del conduttore
l
resistivit à del materiale
0 1 T T0
coefficiente di temperatura
In generale, abbassando la temperatura, la resistenza dei conduttori diminuisce. In certi
casi specifici, a temperature molto vicine allo zero assoluto, la resistenza elettrica
improvvisamente diventa zero. Questi materiali sono detti superconduttori. In materiali
come il Germanio o il Silicio invece la resistenza elettrica diminuisce con l’aumentare
della temperatura.
Corrente e resistenza Cap. 27 HRW
6
Componenti circuitali primarie
Un circuito, qualsiasi esso sia, può essere scomposto in un insieme
(anche estremamente complesso) di componenti semplici:
• Generatori DV
• Capacità C
• Resistenze R
• Induttanze L
Ciascuno di questi componenti risponde in maniera caratteristica
ad una corrente elettrica. Tuttavia qualsiasi circuito elettrico deve
rispettare le proprietà basilari del campo elettrico, il fatto cioè che
la carica si conserva e che il campo è conservativo.
I Legge di Kirchoff
La somma dei valori assoluti delle correnti che entrano in un nodo è
uguale alla somma dei valori assoluti delle intensità di correnti che
escono dal nodo
II legge di Kirchoff
Lungo una maglia la somma delle cadute di potenziale è uguale alla
somma degli aumenti di potenziale
i1
i0
Vdl 0
linea chiusa
i2
i0 i1 i2
Corrente e resistenza Cap. 27 HRW
7
Resistenza
La resistenza è definita come la costante di proporzionalità tra la
corrente e la differenza di potenziale applicato.
l
R
S
DV RI
Resistenze in serie
RTot
RTot R1 R2
Resistenze in parallelo
RTot
Corrente e resistenza Cap. 27 HRW
RTot
1
1
R1 R2
8
1
Condensatore
Un condensatore è un dispositivo capace di immagazzinare carica
elettrica ed è costituito da due conduttori, dette armature poste
l’uno vicino all’altro, ma senza che si tocchino..
Condensatore a
Piatti Piani Paralleli
Condensatore
Sferico
Condensatore
cilindrico
Su entrambe le armature è presente la medesima quantità di carica ma
opposta in polarità
L’osservabile che mi quantifica quanto efficacemente un condensatore è
in grado di immagazzinare carica è data dal rapporto tra la carica presente
sulle armature e la differenza di potenziale corrispondente. Tale rapporto è
definito capacità
Q
C
DV
Coul
C
farad
Volt
Se all’interno delle armature di un condensatore, pongo un dielettico di
costante dielettrica er, la sua capacità aumenta dello stesso fattore
Corrente e resistenza Cap. 27 HRW
9
Capacità in parallelo
Qo Q1 Q2
DV0 DV1 DV2
Co
Qo
Q
Q
1 2 C1 C2
DV0 DV1 DV2
Corrente e resistenza Cap. 27 HRW
10
Capacità in Serie
Qo Q1 Q2
DV0 DV1 DV2
1
Qo
Q0
1
Co
DV0 DV1 DV2 C1 C2
Corrente e resistenza Cap. 27 HRW
1
11
Obiettivi generali degli esercizi (aula/tutor.):
Saper calcolare la resistenza equivalente per due o più
resistenze in serie/parallelo;
Saper calcolare la capacità equivalente per due o più
condensatori in serie/parallelo;
Saper applicare la legge di Ohm.
Corrente e resistenza Cap. 27 HRW
12












