1. La caduta libera
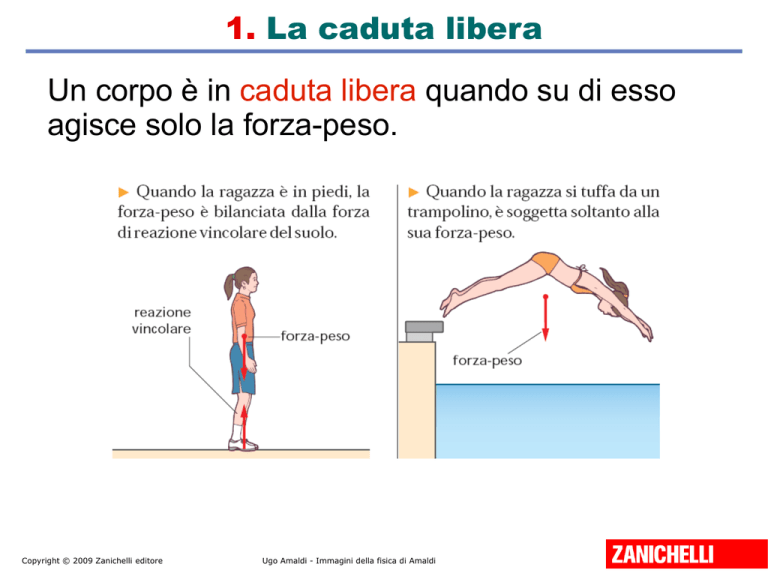
Un corpo è in caduta libera quando su di esso
agisce solo la forza-peso.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La caduta libera
Tutti i corpi in caduta libera subiscono la stessa
accelerazione di gravità costante:
al livello del mare g = 9,8 m/s2.
Per il secondo principio della dinamica la forzapeso è:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La caduta libera
Quindi, se non ci fosse l'attrito dell'aria, tutti i corpi
cadrebbero con lo stesso moto uniformemente
accelerato, a differenza di quanto si osserva
quotidianamente.
Nell'antichità si credeva che la
velocità di caduta dipendesse
dalla massa degli oggetti e che
il moto cessasse al
cessare della forza motrice.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
2. La forza-peso e la massa
La forza-peso è direttamente proporzionale alla
massa dei corpi e all'accelerazione di gravità.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La forza-peso e la massa
La forza-peso dipende dal luogo, mentre la
massa di un oggetto non cambia.
La massa è una proprietà invariante.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La forza-peso e la massa
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La bilancia a bracci uguali
E' una leva di primo genere, dove:
b =b ;
R
M
F = forza-peso da misurare;
R
F = forza-peso dei campioni.
M
All'equilibrio:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
3. La discesa lungo un piano inclinato
Analogamente al caso dell'equilibrio:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La discesa lungo un piano inclinato
F// costante dunque il moto è uniformemente
accelerato, a è diretta lungo il piano:
a aumenta al
crescere
dell'inclinazione.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
4. Il moto dei proiettili
E' il moto di un corpo che riceve solamente una
spinta iniziale:
Dopo il lancio, sul proiettile agisce solo la forzapeso.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il moto dei proiettili - velocità iniziale verso l'alto
L'oggetto tende a salire per inerzia, ma è
rallentato dalla forza-peso.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il moto dei proiettili - velocità iniziale orizzontale
L'unica forza agente ha direzione verticale, perciò
il moto è la sovrapposizione di due moti:
moto rettilineo uniforme in direzione orizzontale
(si applica il I principio);
moto rettilineo uniformemente accelerato in
direzione verticale (si applica il II principio).
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il moto dei proiettili - velocità iniziale orizzontale
La traiettoria è una parabola.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il moto dei proiettili - velocità iniziale orizzontale
La traiettoria è una parabola con vertice nell'origine e
concavità verso il basso. Confrontiamo la caduta di due
palline, una lanciata orizzontalmente e una no.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il moto dei proiettili - velocità iniziale obliqua
Si scompone la velocità iniziale in due vettori,
uno orizzontale e uno verticale.
C'è ancora sovrapposizione di due moti, ma c'è
velocità iniziale in entrambe le direzioni.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il moto dei proiettili - velocità iniziale obliqua
La traiettoria è sempre una parabola, di
equazione:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La gittata
La gittata è la distanza che separa il punto di
partenza dal punto di arrivo al suolo del
proiettile.
La gittata aumenta con l'aumentare dell'angolo
di lancio , raggiunge un massimo per =45°,
poi di nuovo diminuisce.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
L'effetto dell'aria
La presenza dell'aria può modificare la traiettoria
dei proiettili per via dell'attrito viscoso.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
5. La forza centripeta
Per fare muovere un oggetto di moto circolare
uniforme bisogna applicare ad esso una forza.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La forza centripeta
La forza centripeta serve a fare variare il vettore
velocità in direzione e verso, ma non in
intensità.
Se viene a mancare la forza centripeta, il corpo
sfugge lungo la retta tangente della velocità
istantanea.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La forza centripeta
La forza centripeta ha cause diverse, ma il suo
effetto è sempre di incurvare la traiettoria.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Espressione della forza centripeta
Ricordiamo
centripeta:
l'espressione
dell'accelerazione
oppure
Per il secondo principio della dinamica F=ma,
perciò la forza centripeta ha valore:
oppure
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
La forza centrifuga apparente
Quando ci troviamo in un'auto in curva, ci
sentiamo spinti verso l'esterno della curva.
L'auto non è un sistema inerziale perché
soggetta alla forza centripeta: i corpi al suo
interno risentono della forza centrifuga,
apparente.
Qui il corpo
continua a
muoversi in
linea retta
(principio
d'inerzia).
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
6. Il moto armonico di una molla
Una pallina vincolata ad una molla è soggetta alla
forza elastica:
per il secondo principio:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il moto armonico di una molla
I vettori accelerazione e spostamento sono
proporzionali e di verso opposto: il moto della
massa+molla è un moto armonico.
ovvero
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il periodo di oscillazione di una molla
Uguagliamo le costanti di proporzionalità tra
accelerazione e spostamento:
poiché =2/T,
a parità di k, T aumenta al crescere di m (carrello
delle masse).
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
7. Il pendolo
E' formato da una pallina appesa a un filo che, per
piccole oscillazioni, si muove di moto armonico.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Dimostrazione del moto armonico per il pendolo
I triangoli ABC e OAD sono simili:
se < 10°, ds;
Ftangente ha verso opposto a s
Il moto è
armonico.
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il periodo del pendolo
E' il tempo necessario a compiere un'oscillazione
completa.
Uguagliando come nel caso
della molla le costanti di
proporzionalità otteniamo:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi
Il periodo del pendolo e l'accelerazione di gravità
Si ottiene:
Il periodo delle piccole oscillazioni non dipende
dall'ampiezza dell'oscillazione (isocronìa).
Invertendo la formula si può utilizzare il pendolo
per misurare g:
Copyright © 2009 Zanichelli editore
Ugo Amaldi - Immagini della fisica di Amaldi