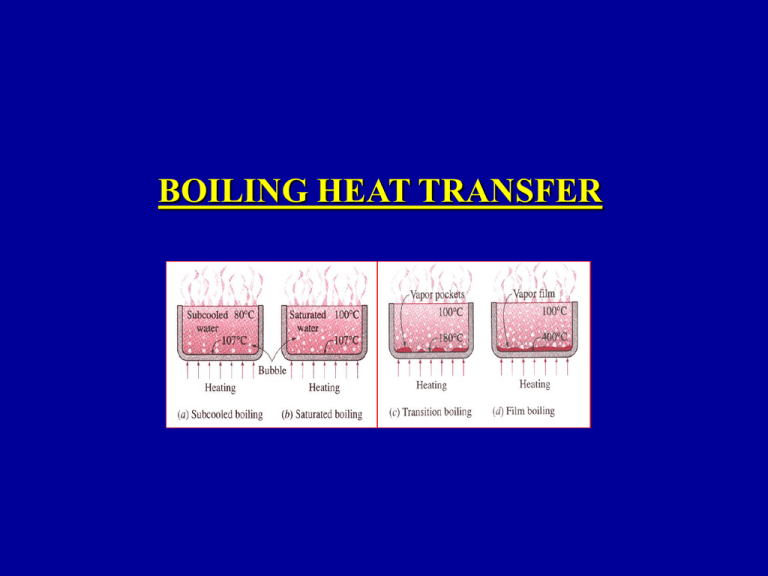
BOILING HEAT TRANSFER
Introduzione all’ebollizione
• La trasmissione del calore per ebollizione è un processo di
scambio termico convettivo accompagnato dal cambiamento
di fase liquido -> vapore.
• Questo cambiamento di fase può avvenire dentro il fluido
puro (nucleazione omogenea) o, più comunemente, in siti di
nucleazione presenti sulla superficie scaldante (cavità) o
dentro il fluido stesso (particelle sospese).
• L’ebollizione è un processo molto efficiente per refrigerare
superfici scaldanti; l’agitazione del liquido circostante causata
dall’ebollizione crea infatti un’azione di pompaggio che
comporta una più efficiente refrigerazione convettiva.
Proprietà termodinamiche e fisiche
• Tensione superficiale (s): è l’energia per unità di area (J/m2)
richiesta per mantenere un’interfaccia liquido-vapore stabile:
è una proprietà dell’interfaccia e dipende dalla natura del liquido e, in
modo meno importante, dalla natura del vapore;
per un liquido puro in contatto con il suo vapore la tensione
superficiale è funzione della sola temperatura.
• Angolo di contatto (bc): è l’angolo tra la superficie solida e
l’interfaccia liquido-gas; essa descrive le caratteristiche bagnanti di
un liquido in relazione ad una data superficie solida ed al gas
circostante.
Vapore
bc
Liquido
Equilibrio e non equilibrio
• Nella termodinamica classica le transizioni di fase sono trattate
come se avvenissero seguendo processi di quasi equilibrio; le reali
transizioni di fase avvengono normalmente sotto condizioni di non
equilibrio. Nei processi di ebollizione una parte del liquido vicino
alla parete scaldante è infatti sempre surriscaldato cioè si trova ad
una temperatura maggiore di quella di saturazione.
• Equilibrio attraverso un’interfaccia sferica:
equilibrio termico:
Tv Tl
equilibrio meccanico: pv pl
equilibrio delle fasi:
g v gl
Liquido
Vapore
2s
r
Equilibrio e non equilibrio
• Dalla relazione di Laplace si vede che per l’esistenza di una bolla di
vapore stabile la pressione del vapore deve essere maggiore di
quella del liquido e questa differenza è tanto più alta quanto più
piccola è la bolla.
• Una buona approssimazione è che la temperatura di equilibrio sia
uguale alla temperatura di saturazione alla pressione della fase
gassosa. Essendo Tl =Tv =Tsat(pv) e pv > pl ne deriva che dovrà essere:
Tl Tsat pv Tsat pl
• Per mantenere in equilibrio una bolla di vapore all’interno della sua
fase liquida, il liquido deve essere surriscaldato della quantità:
Tsat Tl Tsat pl Tv Tsat pl
Equilibrio e non equilibrio
• Per correlare la pressione differenziale liquido-vapore al
surriscaldamento del liquido occorre utilizzare l’equazione di
Clausius-Clapeyron:
2
T v fg
dT
Tv Tsat pl Tsat pl v fg
R Tsat
2s
Tsat
h fg
pv pl
h fg
M v h fg pv r
d p sat
• Se all’interno della bolla vi è del gas incondensabile allora il
surriscaldamento necessario per la fase liquida affinché ci sia
coesistenza vale:
Tsat
2
R Tsat
2s
pn
M v h fg pv r
• Nel caso di nucleazione omogenea il surriscaldamento risulta molto
elevato. Per l’acqua alla pressione atmosferica il surriscaldamento è
di circa 200 °C e l’ebollizione ha una natura esplosiva.
Processo di nucleazione superficiale di una bolla
• Nel caso che il surriscaldamento sia in eccesso la bolla inizierà a crescere;
la crescita all’inizio è piuttosto veloce perché come la bolla cresce 1/r
decresce e l’eccesso di surriscaldamento aumenta.
• Nella posizione 2 l’interfaccia della bolla
raggiunge la sommità della cavità. Da
questo punto in poi la crescita della bolla
diventa piuttosto lenta in quanto il centro di
curvatura si sposta verso l’alto e 1/r
aumenta.
• Il punto critico della crescita della bolla è la
posizione 3 in cui il raggio della bolla
diventa uguale al raggio della cavità. Se il
surriscaldamento locale del liquido eccede
quello richiesto per la configurazione 3 la
bolla cresce molto rapidamente e si distacca
dalla superficie scaldante.
Nucleazione omogenea - stato metastabile
• La condizione di metastabilità può essere spiegata in modo qualitativo
facendo uso dell’equazione di stato di van der Waals che predice isoterme
con l’andamento mostrato in figura.
2
3 pcrit vcrit
RT
p
v vcrit / 3
v2
• Il tratto BC rappresenta una
condizione di metastabilità nella
quale la fase liquida è surriscaldata.
• Il tratto EF rappresenta una
condizione di metastabilità nella
quale
la
fase
vapore
è
sottoraffreddata.
• Il tratto CE è una regione instabile
perché risulta:
p
0
v T
Curva di pool boiling (acqua a pressione atmosferica)
• Nella figura è riportata la tipica curva (biligaritmica) di ebollizione (o di
Nukiyama) per una superficie scaldante immersa in acqua stagnante. Essa
è normalmente divisa in quattro regioni: convezione naturale, ebollizione
nucleata, transizione, ebollizione a film.
Pool boiling, ebollizione nucleata
• La più popolare correlazione di scambio termico in ebollizione nucleata è
stata proposta nel 1952 da Rohsenow:
g l v
l h fg
qNB
s
1/ 2
c pl Tw Tsat
n
C
h
Pr
sf fg
3
dove Csf ed n sono coefficienti che dipendono dal tipo di fluido e dalla
superficie scaldante; per acqua su superficie di acciaio inox pulita si ha
Csf = 0.013 e n = 1.0.
• La transizione dall’ebollizione nucleata a quella a film, se lo scambio
termico avviene a flusso termico imposto, può essere molto pericolosa in
quanto comporta un repentino aumento della temperatura della superficie
scaldante che può provocare dei danni alla stessa (burnout phenomenon).
Pool boiling, flusso termico critico
• Nel progetto di un’apparecchiatura in cui avviene lo scambio termico per
ebollizione è importante per il progettista conoscere il flusso termico critico
in modo da evitare il danneggiamento del componente.
• Il flusso termico critico nel caso di pool boiling può essere, ad es., calcolato
mediante la correlazione semiempirica di Kutateladze (1951):
Ccr h fg s g v2 l v
qCHF
1/ 4
3.0E+06
dove Ccr è una costante il cui
valore
dipende
dalla
geometria della superficie
scaldante; per una grande
superficie piana orizzontale
Ccr = 0.149.
qCHF [W/m2]
2.5E+06
2.0E+06
1.5E+06
1.0E+06
5.0E+05
0.0E+00
0.0
1.0
2.0
3.0
4.0
Pressione [bar]
5.0
6.0
Pool boiling, ebollizione a film
• Nella regione di ebollizione a film la superficie del riscaldatore è
completamente coperta da un film di vapore.
• Usando un’analisi simile alla teoria di Nusselt per la condensazione a film,
Bromley ha sviluppato una teoria per la valutazione del flusso termico
nell’ebollizione a film sull’esterno di un cilindro orizzontale di diametro D:
T
g 2v v l v h fg 0.4 c pv Tw Tsat
0.82
qfilm
D
T
T
v
w
sat
1/ 4
w
Tsat
dove le proprietà del vapore sono da valutare alla temperatura di film
Tf =(Tw+Tsat)/2
• Ad alte temperature della superficie (tipicamente sopra i 300 °C) la
trasmissione del calore avviene anche grazie al contributo
dell’irraggiamento:
3
4
qfilm
qrad
qfilm
s Tw4 Tsat
qtot
4
Flow boiling, definizioni
• Nei processi di ebollizione (condensazione) all’interno di
canali il vapore ed il liquido sono in moto simultaneo
all’interno del canale stesso. Il risultante flusso bifase viene
chiamato flow boiling; esso rappresenta un particolare flusso
bifase.
• Per lo studio del flusso bifase si fa uso di definizioni e
terminologie particolari di seguito brevemente richiamate.
• La frazione di vuoto a è definita come il rapporto tra l’area
della sezione trasversale occupata dal vapore e l’area totale
della sezione trasversale del tubo:
a
Av
A
• La portata massica di fluido che attraversa una
certa sezione del canale, G, è somma della portata
massica di vapore, Gv, e di quella del liquido, Gl.
Flow boiling, definizioni
• Il titolo (dinamico) x è definito come il rapporto tra la portata massica di
vapore che attraversa una sezione trasversale e la portata totale di fluido
che attraversa la stessa sezione.
1
Gv
x
Gv Gl
a
• Lo scorrimento S tra le due fasi (slip
ratio) è definito come il rapporto tra la
velocità media (su Av) della fase vapore e
la velocità media (su Al) della fase
liquida.
S wv / wl
p/pcr
S=1
0
0
x
1
• La frazione di vuoto, il titolo e lo scorrimento sono legati tra loro attraverso
la relazione fondamentale della termodinamica.
a
1
1 x v
1
S
x l
Flow boiling, definizioni
• La velocità superficiale j di una fase è definita come la portata volumetrica
di quella fase divisa per l’area totale della sezione trasversale. Essa
corrisponde alla velocità che ciascuna fase avrebbe se fluisse da sola
all’interno del canale.
jv
Gv
wv a
v A
jl
Gl
wl 1 a
l A
• Il titolo termodinamico (di equilibrio) xth di un fluido in flusso bifase è
definito nel seguente modo:
xth
hTP h f
h fg
dove
hTP x hv 1 x hl
Quando le fasi liquido e vapore sono in equilibrio termodinamico tra loro,
cioè si trovano entrambi alla temperatura di saturazione, il titolo
termodinamico coincide con il titolo.
Flow boiling, canale bollente
• La frazione di vuoto (e la pressione) influisce notevolmente sulle caratteristiche di
moderazione e quindi sul fattore di moltiplicazione dei reattori ad acqua bollente. In
un BWR in condizioni di normale funzionamento la frazione di vuoto media nel
core è di circa il 60%. Un aumento di potenza termica e quindi di a comporta un
aumento delle catture di risonanza dei neutroni durante il loro rallentamento
(p diminuisce) ed una diminuzione degli assorbimenti parassiti dei neutroni termici
(f aumenta). Globalmente il solo aumento della frazione di vuoto comporta una
riduzione del fattore di moltiplicazione.
• Nella tecnologia dei BWRs il termine
canale bollente sta ad indicare la zona di
interesse di una barretta di combustibile di
uno dei circa 750 elementi di combustibile
presenti nel core.
• Un bilancio energetico nel core di un BWR
consente di ricavare il titolo in uscita dal
core (Gcore=13000 kg/s):
Q core Gcore c p Tsub xexit h fg
Flow boiling, flusso verticale verso l’alto
• I possibili regimi di flusso bifase per flusso verticale verso l’alto in un tubo
sono mostrati in figura.
a basso titolo ci si trova, generalmente, nel regime di flusso a bolle;
a valori di titolo maggiori le piccole bolle coalescono in tappi che coprono quasi
tutta la sezione trasversale del tubo (si parla in tal caso di flusso a tappi);
se si parte dal flusso a tappi e si aumenta la portata di vapore si può avere la
rottura dei tappi di vapore portando ad un flusso instabile chiamato churn flow
(flusso agitato).
ad alti livelli di titolo il flusso bifase assume, generalmente, una configurazione
anulare (flusso anulare); l’interfaccia può diventare instabile portando alla
formazione di onde con gocce di liquido che finiscono nel core di vapore;
se si parte dal flusso anulare e si
aumenta la portata del liquido
aumenta la concentrazione delle
gocce presenti nel core di vapore;
queste possono coalescere e portare
alla formazione di ciuffi di liquido
(wispy annular flow).
Flow boiling, mappa dei regimi di flusso
• L’individuazione del regime di flusso bifase presente in una certa
condizione può essere effettuata mediante una mappa dei regimi di flusso
come quella Hewitt e Roberts (1969), relativa al flusso bifase verticale.
Flow boiling, flusso orizzontale
• I possibili regimi di flusso bifase per flusso orizzontale in un tubo cilindrico
sono mostrati in figura. Una delle principali differenze rispetto ai regimi di
flusso verticali è la tendenza di stratificazione del flusso.
Flooding e flow reversal
• Il flooding ed il flow reversal sono fenomeni incontrati in molte condizioni
termoidrauliche dei reattori nucleari, che comprendono transizioni di
regimi di flusso e ribagnamento (rewetting) di superfici calde a seguito di
una perdita incidentale di fluido refrigerante.
• Il termine flooding sta ad indicare la condizione di stallo
di un liquido fluente dall’alto verso il basso causato da
una sufficiente portata di gas fluente dal basso verso
l’alto.
ingresso
liquido
uscita
liquido
GAS
ingresso
liquido
GAS
• Il termine flow reversal sta ad indicare la condizione
nella quale inizia la variazione della direzione del flusso
di liquido, inizialmente in equicorrente con un flusso di
gas che procede dal basso verso l’alto.
Flow boiling, regioni di scambio termico
• Nella figura a lato sono riportati i regimi
di flusso bifase e le regioni di scambio
termico presenti in un canale bollente
con flusso termico costante imposto.
• La transizione dall’ebollizione nucleata
sottoraffreddata (regione B) a quella
satura (regione C) si verifica quando
xth = 0, cioè quando la temperatura di
miscelamento in tazza coincide con
quella di saturazione a quella pressione.
Xth=1
• Nella regione E ed F (flusso anulare) il
processo di ebollizione è rimpiazzato dal
processo di evaporazione all’interfaccia
liquido-vapore.
• Il completo prosciugamento del film di
liquido (DRYOUT) è accompagnato da
un brusco aumento della temperatura di
parete.
Xth=0
Flow boiling, correlazioni di scambio termico
• Una delle più note correlazioni per il calcolo del coefficiente di scambio
termico bifase, applicabile nell’intero intervallo di ebollizione satura, è la
correlazione di Chen (1963):
a 2 a DB F a FZ S
k 0f .79 c 0pf.45 0f .49
k f G 1 x Dh f c p , f
0.24
0.75
0.023
p sat Tw p f
S
F 0.00122 0.5 0.29 0.24 0.24 Tw Tsat p f
Dh A f
k f
s f h fg g
0.8
a 2
q a 2 Tw Tsat
F 1; S 1
0.4
a DB
a FZ
1
F
0.736
2.35 0.213 1 / X tt
1 x
X tt
x
se 1 / X tt 0.1
se 1 / X tt 0.1
0.9
g
f
0.5
f
g
S
1 2.53 106 Re l F 1.25
0.1
;
1
Re l
1.17
G 1 x Dh
Af
• E’ valida sia per fluidi bifase in moto verticale verso l’alto che verso il basso
e, per l’acqua, nel seguente intervallo di condizioni :
Pressione : da 0.17 a 3.5 MPa
Velocità in ingresso del liquido : da 0.06 a 4.5 m/s
2
Flusso termico : fino a 2.4 MW/m
Titolo termodina mico : da 0 a 0.7
Flow boiling, flusso termico critico (CHF)
• Il termine CHF viene utilizzato per indicare una situazione nella quale il
coefficiente di scambio termico di un flusso bifase diminuisce bruscamente
(di circa 1 o 2 ordini di grandezza)
rispetto ai valori ottenuti nel regime
di ebollizione nucleata).
• Se il flusso termico imposto è
relativamente alto è possibile che il
rateo di generazione di vapore nel
regime dell’ebollizione nucleata sia
così elevato da venirsi a creare un
film di vapore che separa il liquido
dalla parete scaldante. Questa
situazione
porta
al
cosiddetto
Departure of Nucleate Boiling (DNB).
• Ad alti valori del titolo la crisi
termica può aversi, con valori più
bassi di flusso termico, per
essiccamento del film di liquido che
bagna la parete (DRYOUT)
Flow boiling, curva di flow boiling
• In figura è possibile confrontare la curva di ebollizione per convezione naturale con la
curva di ebollizione per convezione forzata all’interno di un canale.
• A seconda del titolo termodinamico si
può avere CHF per DNB (sottoraffreddato o saturo) o per DRYOUT.
Flow boiling, flusso termico critico
f p ,G ,Tsub in , Dh , L
qCHF
PWRs (DNB)
BWRs (DRYOUT)
Flow boiling, flusso termico critico
Flow boiling, gradiente di pressione
• L’equazione generalizzata di Bernoulli per un flusso monodimensionale in
regime stazionario all’interno di un canale è:
dp
a
2g
dw 2 dz dh dhA
• Con semplici manipolazioni è
possibile ricavare il gradiente di
pressione lungo il canale come
somma di tre contributi:
d p d w2
d hA
g
g sin
ds 2 ds
ds
• Per un flusso bifase monodimensionale in regime stazionario all’interno di
un canale a sezione costante il gradiente di pressione è dato da:
dp dp
G 2 d vTP dp
dp
dp
2
TP g sin
ds ds acc. spaz. ds att. ds gr . A d s
ds att.
Flow boiling, gradiente di pressione
• Secondo un approccio classico il gradiente di pressione per attrito nel caso
bifase viene correlato ad un opportuno gradiente di pressione per attrito
monofase attraverso un fattore moltiplicatore (moltiplicatore bifase):
lo G 2
dp
dp
2
2
lo
lo
Dh 2 A2 l
ds att. ds att.
TP
LO
dove
LO
dp
ds att.
è il gradiente di pressione per
attrito che si avrebbe se il
flusso bifase scorresse nel tubo
con le proprietà fisiche del
liquido. Il parametro lo2 è detto
moltiplicatore bifase.
Moltiplicatore bifase di Martinelli-Nelson
(valido per acqua)
Flow boiling, gradiente di pressione
• Per a = x = 0 a s = 0 e per un flusso termico imposto e costante attraverso le
pareti di un tubo di lunghezza L, il titolo del vapore aumenta linearmente
con s ed i tre contributi al calcolo della caduta di pressione risultano:
p
TP
att.
lo
G2
Dh 2 A2 l
p
TP
acc. sp.
p
TP
gr .
L
0
L G2 1
ds lo
Dh 2 A2 l xout
2
lo
xout
0
dx
2
lo
2
2
xout
l
G 2 1 xout
2
1
A l 1 a out a out v
1
L l g sin
xout
xout
0
v
1 1 a dx
l
• I termini tra parentesi quadra che compaiono nelle tre relazioni precedenti
sono normalmente graficati in funzione della pressione e del titolo all’uscita.