Elementi
fondamentali della
GEOMETRIA
A
B
r
C
s
A
O
P
B
t
β
D
r
P
Q
d
Per un punto passano
infinite rette
s
u
c
t
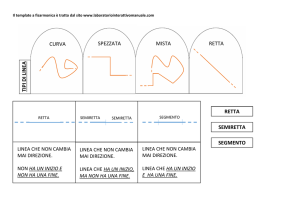
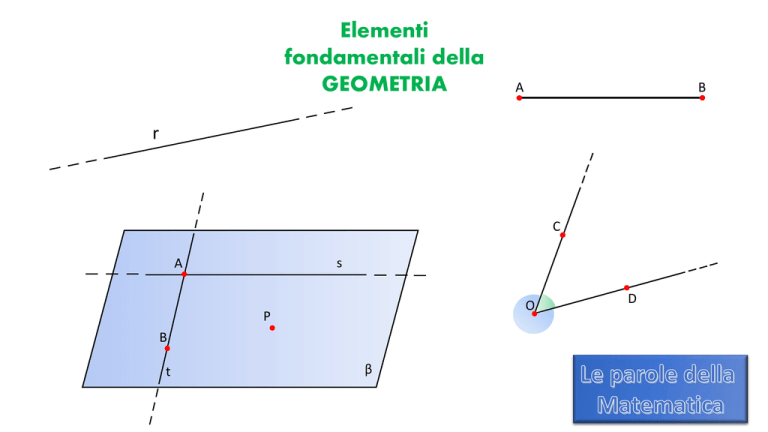
• La retta è un elemento geometrico fondamentale.
Essa è illimitata: non ha né origine né termine.
• Le rette si indicano con le lettere minuscole
dell’alfabeto: a, b, c, …, r, s, …
Tre o più punti sono
allineati quando
appartengono alla
stessa retta
A
B
C
f
Per due punti
distinti passa una
sola retta
Due rette che hanno
in comune un solo
punto si dicono
secanti o incidenti
Due rette sono perpendicolari
quando hanno un punto in comune
e formano quattro angoli retti
r
r
Data una retta r e un punto qualunque P, esiste una e una
sola retta s passante per P e perpendicolare a s.
non
perpendicolari
┴s
s
s
P
O
s
Due rette s e t che sono
entrambe perpendicolari a
una terza retta r non si
intersecano
r
t
r
perpendicolare
Due rette di un piano che non si
intersecano sono parallele
Data una retta r e un punto P non appartenente a
essa, esiste una e una sola retta passante per P e
parallela a r
r // s
P
r
s
t
r
Due rette r e t, parallele a una stessa
retta s, sono parallele tra loro
h┴f
h┴g
allora f // g
Due rette perpendicolari a una
terza retta sono parallele tra
loro
h
t
f
r
s
g
B
L
Due segmenti sono
distinti quando non
hanno alcun punto in
comune
K
P
H
A
C
Due segmenti sono
incidenti se hanno in
comune un punto
che non è estremo
dei segmenti
D
M
B
Il segmento è la parte di retta
compresa tra due punti distinti. I
punti si dicono estremi del segmento
Due segmenti sono adiacenti
quando sono consecutivi e
appartengono alla stessa retta
A
Due segmenti sono
consecutivi quando hanno un
estremo in comune
F
C
G
H
La retta che contiene due punti di un
piano è interamente contenuta nel
piano
Un piano è individuato da tre punti
non allineati
B
C
A
δ
α
Un piano è individuato da una
retta e da un punto che non
appartiene alla retta
• Il piano è un elemento geometrico fondamentale.
Esso è illimitato.
• I piani vengono indicati con le prime lettere
dell’alfabeto greco: α, β, γ, δ, ε.
Ogni retta r di un piano lo divide in due semipiani e
la retta r si dice origine dei due semmipiani
G
F
H
r
r
β
γ
Un angolo si dice concavo
quando contiene i
prolungamenti dei suoi lati
A
β
angolo
convesso
α
o
Un angolo si dice
convesso quando
non contiene i
prolungamenti dei
suoi lati
Due angoli sono consecutivi
quando hanno un lato in comune
e gli altri due lati sono situati da
parti opposte rispetto al lato
comune
A
B
O
C
angolo
concavo
B
Un angolo è ciascuna delle due parti di piano
individuate da due semirette che hanno la
stessa origine
Due angoli consecutivi sono
adiacenti quando i due lati non
comuni giacciono sulla stessa
retta
A
O
B
D
B
F
A
O
C
angoli non
opposti al
vertice
H
C
E
G
I
Due angoli sono
opposti al
vertice quando i
lati di un angolo
sono il
prolungamento
dei lati dell’altro.
I due angoli
sono congruenti
Un angolo retto è metà
di un angolo piatto
Un angolo piatto è delimitato da due
semirette che sono il prolungamento
l’una dell’altra
A
Un angolo giro è un angolo formato da
due semirette sovrapposte aventi la stessa
origine
Punto
Segmenti consecutivi
Ente geometrico fondamentale privo di dimensioni.
Segmenti che hanno solamente un estremo in comune.
Retta
Ente geometrico fondamentale con una sola dimensione
Piano
Ente geometrico fondamentale con due dimensioni: la
lunghezza e la larghezza
Semiretta
Ciascuna delle due parti in cui una retta è divisa da un suo
punto, detto origine delle semirette
Segmento
Figura formata da due punti distinti, A e B, di una retta e dai
punti della retta compresi fra A e B.
I punti A e B sono detti estremidel segmento.
Segmenti adiacenti
Segmenti consecutivi che appartengono alla stessa retta.
Punto medio di un segmento
Punto che divide il segmento in due parti congruenti.
Angolo
Angolo giro
Ciascuna delle due parti in cui un piano è diviso da due
semirette (lati), aventi un’origine in comune (vertice).
Angolo i cui lati coincidono e che contiene tutti i punti
del piano.
Angolo convesso
Angolo piatto
Angolo che non contiene i prolungamenti dei suoi lati.
Angolo concavo
Angolo che contiene i prolungamenti dei suoi lati.
Bisettrice
Semiretta che ha origine nel vertice dell’angolo e lo
divide in due parti congruenti.
Angolo nullo
Angolo privo di punti interni.
Angolo i cui lati sono semirette opposte.
Angolo retto
Metà di un angolo piatto.
Angolo acuto
Angolo minore di un angolo retto.
Angolo ottuso
Angolo maggiore di un angolo retto e minore di un angolo
piatto.
Angoli consecutivi
Angoli esplementari
Angoli che hanno soltanto un lato e il vertice in comune. Angoli la cui somma è un angolo giro.
Angoli adiacenti
Angoli consecutivi i cui lati non comuni sono due
semirette opposte.
Angoli opposti al vertice
Angoli tali che i lati dell’uno sono le semirette opposte
dei lati dell’altro.
Angoli complementari
Grado ( ° )
Angoli la cui somma è un angolo retto.
Unità di misura fondamentale dell’ampiezza degli angoli.
E’ la 360a parte dell’angolo giro.
Angoli supplementari
Angoli la cui somma è un angolo piatto.
Primo ( ‘ )
Sottomultiplo del grado: 1° = 60’
Secondo ( ʺ )
Sottomultiplo del grado: 1° = 3600ʺ; 1’ = 60ʺ
Rette complanari
Rette coincidenti
Rette che giacciono sullo stesso piano.
Rette che hanno tutti i punti in comune
Rette incidenti
Distanza di un punto da una retta
Rette che hanno un solo punto in comune.
Segmento perpendicolare condotto dal punto alla retta.
Rette perpendicolari
Asse (di un segmento)
Rette incidenti che formano quattro angoli retti.
Retta perpendicolare al segmento nel suo punto medio.
Rette parallele
Distanza di due rette parallele
Rette che non hanno alcun punto in comune.
Distanza di un qualsiasi punto di una di esse dall’altra.
r