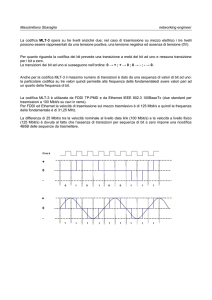
Codifica di linea
• La rappresentazione di dati numerici con segnali numerici
e’ normalmente fatta tramite sequenze di impulsi discreti
di tensione di una certa durata temporale
• Il dato binario e’ codificato in modo da far corrispondere
al valore di un bit un determinato livello del segnale
• Il ricevitore deve sapere quando inizia e finisce il bit,
leggere il valore del segnale al momento giusto,
determinare il valore del bit in base alla codifica utilizzata
– questa funzione si chiama sincronizzazione
– la migliore valutazione si ottiene leggendo il valore del
segnale nell’istante corrispondente a meta’ bit
Caratteristiche delle codifiche di linea
• Sono possibili diverse scelte di codifica, con
caratteristiche differenti che possono migliorare le
prestazioni della trasmissione
• Le caratteristiche determinanti sono:
– spettro del segnale
– sincronizzazione temporale: il ricevitore deve essere
sincronizzato con il trasmettitore per identificare i bit;
alcune codifiche facilitano questa funzione
– rilevazione di errore: funzione caratteristica dei livelli
superiori, ma puo’ essere utile anche a livello fisico
– solidita’ del segnale rispetto ad interferenza o rumore
– costo e complessita’ di realizzazione
Principali codici di linea binari
Effetto della limitazione di banda
Effetto dell’ISI sugli impulsi
Diagramma ad occhio
Segnalazione binaria e M-aria/multilivello
Esempi di segnalazione multilivello
Diagramma ad occhio
Relazione codifica binaria/M-aria
M=2k
Wb=Rb(1+β)/2
Rs=Rb/k
WM=Rs(1+β)/2=Rb(1+β)/2k
Ts=Tb*k
k=Log2(M)
WM=Wb/Log2(M)
Relazione BER e SER: codifica binaria
naturale e di Gray
Alfabeto (M=8)
Codice naturale
Codice di Gray
X1
X2
X3
X4
X5
X6
X7
X8
000
001
010
011
100
101
110
111
000
001
011
010
110
111
101
100
Codice
Naturale
Codice di Gray
SER*M/2(M-1)
SER/Log2(M)
BER
BER (M>>1)
SER/2
BER (M=16)
SER/2
Per M>> 1
SER/4
BERGRAY = BERNAT*[2/Log2(M)]
Codifica di linea differenziale
Ripetitori/rigeneratori di segnali PCM
Ripetitore rigenerativo
Estrazione del segnale di clock
Teorema di Shannon-Hartley sulla
capacità di un canale AWGN
R< C
C=W*Log2(1+S/N)
C/W=Log2(1+Eb*R/No*W)
Per W infinito:
C=1,44(S/No)
C/B al variare di S/N