Media – Varianza – Deviazione Standard

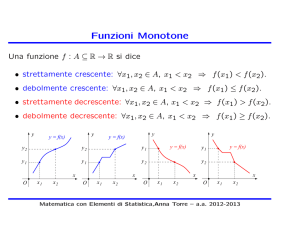
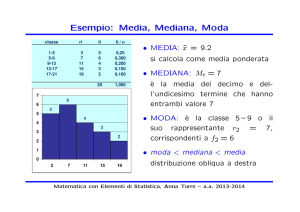
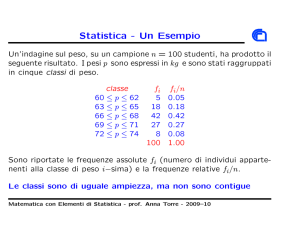
Media – Varianza – Deviazione Standard
x̄ media
n
1 X
·
xi
n i=1
m
1 X
·
fi xi
n i=1
s2 varianza
n
1 X
·
(xi − x̄)2
n i=1
m
1 X
·
fi · (xi − x̄)2
n i=1
s dev. standard
v
u
n
u1 X
t ·
(xi − x̄)2
n i=1
v
u
m
u1 X
t ·
fi · (xi − x̄)2
n i=1
s2
n
X
1
·
(xi − x̄)2
n − 1 i=1
m
X
1
·
fi · (xi − x̄)2
n − 1 i=1
v
u
u
t
v
u
u
t
campionaria
s2 campionaria
n
X
1
·
(xi − x̄)2
n − 1 i=1
m
X
1
·
fi · (xi − x̄)2
n − 1 i=1
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Varianza – Deviazione Standard
Le espressioni della varianza (e della deviazione standard) possono
essere riscritte come segue:
1
2
s = ·
n
X
n
i=1
2
x2
i − n x̄
o
1
2
s = ·
n
X
m
i=1
2
fi x2
i − n x̄
Infatti,
n
X
i=1
(xi − x̄)2
=
=
n
X
2) =
(x2
−
2x
x̄
+
x̄
i
i
i=1
2
x2
i − 2x̄(n x̄) + n x̄ =
i=1
n
X
n
X
i=1
x2
i − 2x̄
n
X
i=1
n
X
xi +
i=1
2
x2
i − n x̄
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
n
X
i=1
x̄2 =
Esercizi
Esercizio 1. Nel rilevare l’altezza in cm di un gruppo di reclute si è ottenuta la
seguente tabella delle frequenze. Calcolare media, mediana e quartili.
Soluzione:
cm
fass
166
1
168
3
169
6
170
11
171
8
172
6
173
4
174
3
175
1
178
1
fcum
1
4
10
21
29
35
39
42
43
44
n = 44 dimensione del campione
x̄ ≃ 170.9 media
x22 + x23
Me =
= 171 mediana
2
x11 + x12
q1 =
= 170 primo quartile
2
x33 + x34
= 172 terzo quartile
q3 =
2
q3 − q1 = 2 distanza interquartile
La distanza interquartile è un altro indice di dispersione, legato alla nozione di
mediana. La mediana suddivide l’insieme dei dati ordinati {xi} in due parti ugualmente numerose. I quartili si ottengono suddividendo i dati ordinati in quattro parti
ugualmente numerose.
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Esercizi
Esercizio 2. Trovare media, mediana, moda, varianza e deviazione
standard dei seguenti dati non ordinati e non raggruppati. Tracciare
l’istogramma delle frequenze.
7 4 10 9 15 12 7 8 11 4 14 10 5 14 1 10 8 12 6 5
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Esercizi
Soluzione: si costruisce la tabella della distribuzione di frequenza
x
fass
x̄ =
2
s
1
1
4
2
5
2
6
1
7
2
8
2
9
1
10
3
11
1
12
2
14
2
15
1
20
1
(1 + 8 + 10 + 6 + 14 + 16 + 9 + 30 + 11 + 24 + 28 + 15) = 8.6
20
1
(57.76 + 42.32 + 25.92 + 6.76 + 5.12 + 0.72 + 0.16 + 5.88+
=
20
+5.76 + 23.12 + 58.33 + 40.96) ≃ 13.64
s ≃ 3.69
moda = 10.0
mediana = 8.5
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Esercizio
Un’indagine su un campione di n = 100 studenti, che hanno sostenuto
la prova scritta di matematica, ha prodotto il seguente risultato. Le
votazioni in centesimi sono state raggruppate in quattro classi.
classe
20 − 40
40 − 60
60 − 80
80 − 100
fi
10
20
50
20
100
fi/n
0.10
0.20
0.50
0.20
1.00
Le classi sono di uguale ampiezza e contigue.
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Esercizio
Nell’ipotesi di distribuzione uniforme, è naturale associare a ciascuna
classe, come rappresentante, il valore centrale ri della classe stessa.
classe
20 − 40
40 − 60
60 − 80
80 − 100
media =
ri
30
50
70
90
fi
10
20
50
20
Fi
10
30
80
100
1
· (10 · 30 + 20 · 50 + 50 · 70 + 20 · 90) = 66
100
mediana = 70 (guardando solo i rappresentanti)
varianza =
1
· (10 · 362 + 20 · 162 + 50 · 42 + 20 · 242) = 21.44
100
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Esercizio
100
50
80
40
60
30
40
20
20
10
20
40
60
80
Poligono delle frequenze
100
20
40
60
80
Ogiva di frequenza
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
100
Esercizio
Calcolo della mediana:
50
40
30
20
10
20
40
60 68
80
100
area totale = 20 · (10 + 20 + 50 + 20) = 2000
Cerchiamo il valore x = Me tale che
20 · 10 + 20 · 20 + (x − 60) · 50 = 1000
⇒
x = 68
⇒
Me = 68
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Esercizio
100
80
60
50
40
20
20
40
60
68
80
100
Calcolo della mediana: interpolazione lineare sui punti A = (60, 30) e B = (80, 80)

y = 50
5
⇒ (50 − 30) = · (x − 60) ⇒ x = 68 ⇒ Me = 68
5
y − 30 = · (x − 60)
2
2
Domande: (a) qual è il voto massimo preso dal 10% degli studenti con i voti
peggiori?
[40]
(b) Calcolare i quartili dall’ogiva di frequenza.
[q1 = 55 , q2 = 78]
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Esercizio
100
100
80
80
60
60
50
40
40
20
25
20
20
40
60
68
80
100
100
100
80
80
75
60
60
40
40
20
20
20
40
55 60
20
40
60
80
100
10
20
40
60
80
100
78
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
100
Distribuzione Normale
• istogramma delle frequenze di un insieme
di misure relative a una grandezza che
può variare con continuità
• popolazione molto numerosa, costituita
da una quantità praticamente illimitata
di individui (popolazione infinita)
• area dell’istogramma uguale a 1 (normalizzata)
• aumentando il numero di intervallini n =
5, 9, 17, . . . l’istogramma tende a stabilizzarsi intorno a una forma limite: la
curva di distribuzione delle frequenze
2
• nel caso in figura: y = Ae−B(x−C)
distribuzione normale o gaussiana
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014
Distribuzione Normale
CURVE GAUSSIANE
y = Ae−B(x−C)
2
Se la distribuzione è di tipo gaussiano con
• media aritmetica µ
• deviazione standard σ
si ha
1
1
√
B =
C = µ
2
2σ
σ 2π
La corrispondente curva normale sarà
A =
y =
1
√
σ 2π
(x − µ)2
−
2σ 2
e
Curva normale standardizzata:
0
2
1
− x2
e
y = √
2π
µ = 0,σ = 1
Matematica con Elementi di Statistica, Anna Torre – a.a. 2013-2014