Appunti di economia e organizzazione aziendale I
La teoria del prezzo di mercato (domanda e offerta di un bene)
Abbiamo accennato nella lezione precedente che il metodo di studio che utilizzeremo in microeconomia è quello
dell’equilibrio economico parziale, sviluppato dall’economista Alfred Marshall, detto metodo della scuola di
Cambridge. E’ opportuno ricordare che questo metodo si basa sul presupposto che nell’analisi di un mercato rimangano
costanti tutte le variabili che stanno al di fuori di quel mercato. In particolare la teoria del prezzo di mercato determina il
prezzo (P) e la quantità (Q) di equilibrio di un mercato, a parità di tutte le altre condizioni, cioè tenendo ferme tutte
quelle grandezze economiche che non siano il prezzo e la quantità scambiata con riferimento a quel mercato (quindi P e
Q di altri mercati, ma anche i salari dello stesso mercato, tasso di interesse, disoccupazione, ecc.).
E’ questa una premessa che non va mai dimenticata.
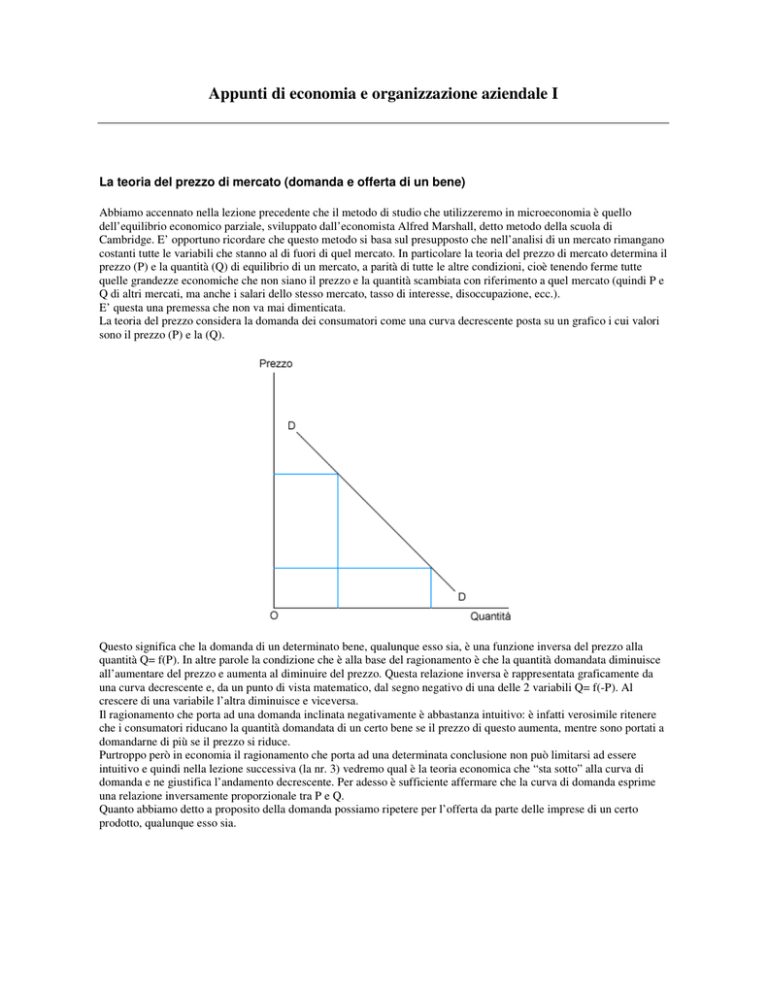
La teoria del prezzo considera la domanda dei consumatori come una curva decrescente posta su un grafico i cui valori
sono il prezzo (P) e la (Q).
Questo significa che la domanda di un determinato bene, qualunque esso sia, è una funzione inversa del prezzo alla
quantità Q= f(P). In altre parole la condizione che è alla base del ragionamento è che la quantità domandata diminuisce
all’aumentare del prezzo e aumenta al diminuire del prezzo. Questa relazione inversa è rappresentata graficamente da
una curva decrescente e, da un punto di vista matematico, dal segno negativo di una delle 2 variabili Q= f(-P). Al
crescere di una variabile l’altra diminuisce e viceversa.
Il ragionamento che porta ad una domanda inclinata negativamente è abbastanza intuitivo: è infatti verosimile ritenere
che i consumatori riducano la quantità domandata di un certo bene se il prezzo di questo aumenta, mentre sono portati a
domandarne di più se il prezzo si riduce.
Purtroppo però in economia il ragionamento che porta ad una determinata conclusione non può limitarsi ad essere
intuitivo e quindi nella lezione successiva (la nr. 3) vedremo qual è la teoria economica che “sta sotto” alla curva di
domanda e ne giustifica l’andamento decrescente. Per adesso è sufficiente affermare che la curva di domanda esprime
una relazione inversamente proporzionale tra P e Q.
Quanto abbiamo detto a proposito della domanda possiamo ripetere per l’offerta da parte delle imprese di un certo
prodotto, qualunque esso sia.
Qui però notiamo che l’andamento della curva di offerta è crescente, perché esprime una relazione diretta tra la quantità
offerta dai produttori e prezzo del bene. Più aumenta il P e più i venditori sono incentivati ad aumentare la quantità
offerta sul mercato e viceversa. Anche questo è un ragionamento abbastanza intuitivo, perché il produttore che vede
salire il P del suo bene è stimolato ad offrirne di più sul mercato, per aumentare il suo guadagno e viceversa in caso di
diminuzione del P. Pure in questo caso però l’andamento crescente della curva d’offerta è spiegato da una teoria
economica, che vedremo nella lezione nr. 4. Da un punto di vista strettamente matematico la relazione diretta tra P e Q
nell’offerta di un bene è espressa dalla funzione Q= g(+P).
A questo punto per giungere alla situazione di equilibrio del mercato è sufficiente mettere insieme le 2 curve di
domanda e offerta nello stesso grafico, ma prima definiamo il concetto di equilibrio di un mercato qualsiasi.
Secondo questa teoria della domanda e dell’offerta, un mercato è in equilibrio quando si determinano un P ed una Q
scambiata che sono stabili, cioè destinati a perdurare nel tempo. Ogni altro valore, non di equilibrio, di queste 2 variabili
(P e Q) comporta un’instabilità del sistema, perché le forze di mercato spingeranno sempre P e Q verso i valori di
equilibrio.
Vediamo ora in concreto come si forma l’equilibrio di mercato.
Nella figura vediamo sia la funzione di domanda (decrescente), sia la funzione d’offerta (crescente).
Ricordiamo che i punti sopra la curva di domanda indicano le quantità domandate dai consumatori, in quel mercato, per
ogni livello di prezzo del bene, mentre i punti sulla curva d’offerta individuano, per ogni prezzo, le quantità che i
venditori sarebbero disposti ad offrire. Ebbene, si dimostra, che la situazione di equilibrio si realizza nell’unico punto
del grafico (E) dove la quantità domandata dai consumatori è la stessa quantità offerta dai venditori a parità di prezzo.
Ovvero c’è equilibrio quando il P è tale per cui le 2 quantità domandate e offerte sono esattamente uguali. Solamente
quando le due grandezze prezzo e quantità assumono i valori P* e Q* il mercato è in equilibrio, cioè stabile, senza
tendenze alla modificazione.
Il punto E è l’unico punto che uguaglia la Q domandata e la Q offerta e determina il prezzo (P*) e la quantità scambiata
(Q*) d’equilibrio. Dal punto di vista grafico questo punto E è quello d’intersezione delle due curve, mentre in ottica
matematica è quello per il quale le due funzioni di domanda e offerta si uguagliano:
(Q= f(-P)) = (Q= g(P)).
Ma perché l’equilibrio del mercato si forma proprio in quel punto ?
La risposta si può desumere dalla seguente figura.
Se il prezzo fosse più alto di quello di equilibrio, per es. P1, ci sarebbe nel mercato un eccesso di offerta,
corrispondente alla distanza tra B e A. In questa situazione si accumulerebbero le scorte di magazzino a causa della
merce invenduta, costringendo i venditori ad ordinare (o produrre) minor quantità di quel bene, per mancanza di
domanda da parte dei consumatori. La restrizione della quantità offerta, accompagnata dal minor prezzo a cui gli
offerenti sarebbero disposti a vendere pur di eliminare le giacenze di magazzino, spingono il mercato verso un prezzo
più basso e precisamente verso il prezzo di equilibrio P*.
Il discorso è analogo, ma speculare, nel caso che il mercato avesse un prezzo più basso di quello di equilibrio, per es.
P2. Nel caso prospettato ci sarebbe un eccesso di domanda, corrispondente alla distanza tra Q2 e Q1. Al prezzo P2
una parte dei consumatori non avrebbe la possibilità di acquistare il bene e vi dovrebbe rinunciare, per cui questi
consumatori, pur di avere il bene che domandano, sono disposti a spendere un po’ di più. L’eccesso di domanda porta
quindi a spinte al rialzo del prezzo, causate dalla mancata soddisfazione di alcuni consumatori. I venditori assecondano
questi consumatori accompagnando l’aumento del prezzo con una maggiore offerta. Tutto ciò porta il mercato ad
aumentare il prezzo, fino a raggiungere quello di equilibrio P*.
In ambedue i casi, le tendenze del mercato si arrestano quando si raggiunge il punto d’intersezione tra le due curve di
domanda e offerta. Solo il prezzo d’equilibrio P*, determinato dal punto E, provoca la stabilità del mercato e causa il
venir meno di spinte al rialzo o al ribasso dei prezzi. L’equilibrio si realizza esclusivamente laddove la quantità
domandata è uguale a quella offerta ed i conseguenti valori del prezzo (P*) e della quantità (Q*) sono gli unici che
stabilizzano il mercato.
• Quando le variazioni riguardano i valori degli assi, cioè prezzo (P) e quantità (Q), allora ci spostiamo sulle curve di
domanda e offerta.
• Quando le variazioni riguardano altre grandezze economiche (il salario, il tasso di disoccupazione, il prezzo di altri
mercati, le quantità domandate o offerte di altri mercati, il tasso d’inflazione, i gusti dei consumatori, ecc.), diverse dal
P e Q di quel mercato, allora c’é lo spostamento (traslazione) delle curve di domanda e offerta. In particolare, la
domanda si sposta verso l’alto e a destra quando cresce (perché a parità di P la quantità domandata è maggiore) e verso
il basso e a sinistra quando diminuisce. L’offerta si sposta verso il basso e a destra quando cresce (perché a parità di P la
quantità offerta è maggiore) e verso l’alto e a sinistra quando diminuisce.
Categorie di beni economici
Diamo ora alcune definizioni di beni economici che saranno molto importanti nelle lezioni successive.
Beni sostituti (o succedanei) e beni complementari.
Due beni sono tra loro sostituti (o succedanei), quando sono così simili da soddisfare in modo equivalente gli stessi
bisogni. Per es. burro e margarina.
Due beni sono invece tra loro complementari, quando sono utilizzati congiuntamente per soddisfare determinati bisogni.
Per es. caffè e zucchero.
Secondo la relazione tra P e Q,
Un bene è sostituto di un altro quando l’aumento del P del primo implica l’aumento della Q domandata (spostamento
della curva di domanda in alto e a destra) del secondo e viceversa.
Un bene è complementare di un altro quando l’aumento del P del primo implica la riduzione della Q domandata
(spostamento della curva di domanda in basso e a sinistra) del secondo e viceversa.
Beni normali e beni inferiori.
La distinzione verte sulla reazione della domanda dei beni alle variazioni del reddito dei consumatori (relazione tra Q e
Reddito).
Un bene è normale se l’aumento del reddito comporta un aumento della sua domanda (spostamento in alto della curva)
e viceversa in caso di diminuzione del reddito.
Un bene è inferiore se l’aumento del reddito comporta una diminuzione della sua domanda (spostamento in basso della
curva) e viceversa in caso di diminuzione del reddito.
Elasticità della domanda e dell’offerta
Un importantissimo concetto, di cui non solo gli economisti, ma anche gli operatori di mercato (venditori e produttori)
dovrebbero sempre tenere conto, è quello di elasticità della curva di domanda o d’offerta.
Diciamo subito che quello che affermeremo sull’elasticità della domanda vale anche per l’elasticità dell’offerta, tuttavia
la più importante in assoluto è sicuramente la prima, perché attraverso la considerazione dell’elasticità della domanda è
possibile trarre, oltre a molte considerazioni di teoria economica, anche notevoli spunti per comprendere il
comportamento dei venditori nelle loro politiche di offerta.
L’elasticità della domanda rispetto al prezzo misura la reattività della quantità domandata ad una variazione percentuale
del prezzo, cioè indica di quanto varia la quantità domandata di un bene se il suo prezzo aumenta o diminuisce di una
certa percentuale.
In termini matematici l’elasticità è rappresentata dal coefficiente davanti alla variabile che si modifica (il prezzo). Per
es. se questa è la funzione della domanda Q= a - bP, l’elasticità è data dal valore di b.
In termini grafici l’elasticità è la pendenza della curva di domanda. Se per es. aumentando il prezzo di una unità, il
nuovo punto sulla curva di domanda, corrispondente al nuovo P, determina una diminuzione della quantità domandata
di 3 unità, l’elasticità della domanda è 3.
In figura sono rappresentate 2 curve di domande con 2 diverse elasticità (pendenze), come possiamo vedere dalla
diversa reazione, in termini di diminuzione della Q domandata, in risposta alla stessa variazione (aumento) di P.
La formula matematica dell’elasticità è questa:
elasticità della domanda =
∆%Q
=(variaz. % della Q domandata) / (variaz. % del P)
∆% P
dove (variaz. % della Q domandata) = (delta Q/Q) x 100 e (variaz. % del P) = (delta P/P) x 100
L’elasticità della domanda rispetto al prezzo può assumere tantissimi valori (ai quali corrispondono curve di domanda
più o meno inclinate).
Una classificazione dei diversi valori di elasticità è la seguente:
a) Elasticità = 0 Non c’è reattività della domanda. Qualsiasi variazione del P lascia indifferente la quantità
domandata. Graficamente la domanda è una retta verticale. Si dice in questo caso che la domanda è rigida o
anelastica.
b) Elasticità = 1 La variazione % del P determina la stessa variazione % della Q domandata.
c) Elasticità < 1 C’è poca reattività della Q alle variazioni di P. L’inclinazione della domanda è vicina a quella
verticale. Si dice che la domanda è poco elastica.
d) Elasticità > 1 C’è molta reattività della Q alle variazioni di P. La pendenza della domanda è vicina a quella
orizzontale. Si dice che la domanda è molto elastica.
e) Elasticità = infinito La reattività è massima. Qualsiasi piccola variazione di P provoca una
grossa risposta della Q domandata. La domanda è una retta orizzontale. La domanda in questo
caso è perfettamente o infinitamente elastica.
Domande infinitamente elastiche non esistono (è un caso limite ipotetico). Esistono però domande rigide (con elasticità
= 0), per esempio la dipendenza di alcuni paesi dall’importazione del petrolio fa considerare la loro domanda per quel
combustibile come rigida. Questo spiega il motivo dell’alto prezzo del petrolio in certi periodi storici: esso era
determinato unicamente dalla variazione dell’offerta (riduzione) da parte delle nazioni arabe produttrici (OPEC).
Un’ultima considerazione.
Quando l’elasticità della domanda di un bene rispetto al prezzo è inferiore a 1, si dice che quel bene è di prima
necessità.
Quando l’elasticità di un bene è maggiore di 1, si dice che quel bene è un bene di lusso.
La curva di Phillips.
In macroeconomia, la curva di Phillips è una (a seconda dei punti di vista, ipotetica) relazione inversa tra inflazione e
disoccupazione.
L'economista britannico A.W. Phillips, nel suo storico contributo del 1958 The relationship between unemployment and
the rate of change of money wages in the UK 1861-1957 («La relazione tra disoccupazione e il tasso di variazione dei
salari monetari nel Regno Unito 1861-1957»), pubblicato su Economica (la rivista della prestigiosa London School of
Economics), osservò una relazione inversa tra variazioni dei salari monetari e livello di disoccupazione nell'economia
britannica, nel periodo preso in esame. Analoghe relazioni vennero presto osservate in altri paesi, e nel 1960 Paul
Samuelson e Robert Solow, a partire dal lavoro di Phillips, proposero una esplicita relazione tra inflazione e
disoccupazione: allorché l'inflazione era elevata, la disoccupazione era modesta, e viceversa.
Non altrettanto noto è che l'economista statunitense Irving Fisher aveva proposto una relazione analoga a quella
osservata da Phillips negli anni '20. D'altra parte, la curva originariamente proposta da Phillips descriveva il
comportamento dei salari monetari (comunque collegati all'inflazione). A motivo di ciò, secondo alcuni la curva di
Phillips dovrebbe essere più propriamente chiamata curva di Fisher.
Negli anni immediatamente successivi al contributo del 1958 di Phillips, diversi economisti nei paesi maggiormente
industrializzati furono convinti che i risultati di Phillips indicassero una relazione stabile, permanente, tra inflazione e
disoccupazione. Un'implicazione di questa conclusione per la politica economica sarebbe che i governi potrebbero
controllare inflazione e disoccupazione, tramite una politica Keynesiana, risolvendo così in generale un problema di
trade-off tra i due obiettivi della politica economica scegliendo un punto sulla curva di Phillips
La curva di Phillips non è altro che l’espressione della scelta fra una minor inflazione o una minor disoccupazione, per
un sistema economico.
Nell’esempio, passando dal punto E al punto E’, cresce l’occupazione e, quindi, migliora il PIL della collettività, ma il
prezzo da pagare è una ben più alta inflazione.
La curva elaborata da Phillips ha avuto un grande seguito per l’importanza pratica che assume. Infatti, essa è stata
utilizzata dai pubblici poteri di tutto il mondo per fissare degli obiettivi di PE che riducessero una delle due grandezze,
compatibilmente con un certo peggioramento dell’altra. In pratica, i governi dei paesi che utilizzano la curva di Phillips,
hanno impostato la propria PE cercando di raggiungere degli obiettivi, in termini di combinazione inflazionedisoccupazione, che rappresentassero il male minore per la collettività. In realtà quello che i pubblici poteri dovrebbero
cercare di ottenere non è il raggiungimento di un certo punto sulla curva che sia accettabile dal paese, ma lo
spostamento della curva stessa verso l’interno (verso l’origine del grafico), in modo da migliorare entrambe le
grandezze economiche: inflazione e disoccupazione. Ciò è possibile mettendo in campo un mix di politiche monetarie e
fiscali, nonché di politiche legate all’offerta (sussidi e incentivi), in grado di indirizzare l’economia verso risultati
possibili e certi, che siano migliorativi di tutte le grandezze economiche in gioco.
TASSAZIONE
Se il governo impone una tassa su un bene, dobbiamo fare attenzione a quello che vogliamo dire quando
parliamo del 'prezzo del bene perché ci sono di fatto due prezzi - il prezzo pagato dagli acquirenti ed il
prezzo ricevuto dai venditori. La differenza tra i due è semplicemente la tassa - presa dal governo. Questa
può essere costante o può variare (dipendendo dal prezzo, per esempio) secondo il genere di tassa che il
governo impone. Se è una tassa 'flat rate' (a tasso piatto) allora la tassa è costante - un determinato
ammontare per ciascuna unità del bene comprata e venduta. Se è una tassa 'ad valorem' - come l'IVA allora aumenta all'aumentare del prezzo. Ci sono altro generi di tassa, ma questi sono i due che
considereremo in questa lezione. Cominciamo con una tassa 'flat rate'. Cominciamo con la posizione prima
che la tassa sia imposta. Per semplicità assumiamo domanda ed offerta lineari - ma l'analisi è la stessa con
altre forme di domanda e offerta. Si può vedere che il prezzo d'equilibrio è 55 e che 45 unità sono scambiate.
Ora supponiamo che il governo imponga una tassa 'flat rate' di 10 per unità del bene comprato e venduto. Questo vuole
dire che il prezzo pagato dall'acquirente è sempre 10 in più rispetto al prezzo ricevuto dal venditore - perché il governo
prende 10 per ciascuna unità comprata e venduta. Cosa significa questo per la domanda e l'offerta? Per prima cosa
notiamo che il punto cruciale per gli acquirenti è il prezzo che pagano e il punto cruciale per i venditori è il prezzo che
ricevono. Nella figura sopra noi non abbiamo avuto bisogno di distinguere tra loro perché senza una tassa questi due
prezzi coincidono. Tuttavia con una tassa dobbiamo essere accurati. Possiamo fare l'analisi con uno dei due prezzi.
Cominciamo col prezzo pagato dagli acquirenti, che è la variabile sull'asse verticale nella figura 27.2. Poiché questa è la
cosa che importa agli acquirenti, la curva di domanda nella figura 27.2 è esattamente la stessa della figura 27.1. Tuttavia
questo non è vero per la curva d'offerta: quello che determina l'offerta è il prezzo ricevuto dai venditori e questo è 10 in
meno (in questo esempio) del prezzo pagato dai compratori. Così per trovare l'offerta a un qualsiasi prezzo pagato dagli
acquirenti abbiamo bisogno di trovare l'offerta a quel prezzo meno la tassa. Così l'effetto sulla curva dell'offerta è
semplice: la muove verso l'alto di una distanza pari all'ammontare della tassa - in questo caso un ammontare costante
pari a 10. Per indurre i venditori ad offrire una data quantità il prezzo pagato dagli acquirenti deve essere 10 in più di
prima.
Il nuovo equilibrio è dove la nuova curva d'offerta e la curva di domanda si intersecano. Possiamo vedere che l'effetto è
di ridurre la quantità scambiata - in questo esempio da 45 a 40 - e aumentare il prezzo d'equilibrio pagato dagli
acquirenti a 60. Da questo possiamo calcolare il nuovo prezzo d'equilibrio ricevuto dai venditori - 10 in meno del
prezzo d'equilibrio pagato dagli acquirenti - e quindi 50.
Alternativamente possiamo lavorare col prezzo ricevuto dai venditori sull'asse verticale. Vediamo la figura 27.3. Poiché
questo prezzo è ciò che importa ai venditori la curva di offerta nella figura 27.3 è la stessa della figura 27.1. Tuttavia la
curva di domanda è diversa perché il prezzo che pagano è uguale al prezzo ricevuto dai venditori più la tassa - in questo
caso 10. Per trovare la domanda ad un qualsiasi dato prezzo ricevuto dai venditori abbiamo bisogno di chiederci cosa
sarebbe la domanda a quel prezzo più la tassa. Possiamo vedere perciò che la curva di domanda nella figura 27.3 è
quella di figura 27.1 spostata in basso di una distanza pari a 10 (l'ammontare della tassa). Per indurre gli acquirenti a
comprare una quantità data, il prezzo ricevuto dai venditori ha bisogno di essere 10 in meno rispetto a prima.
Il nuovo equilibrio è dove la nuova curva d'offerta e la curva di domanda si intersecano. Possiamo vedere che l'effetto è
di ridurre la quantità scambiata - in questo esempio da 45 a 40 - e diminuire il prezzo d'equilibrio pagato ai venditori a
50. Da questo possiamo calcolare il nuovo prezzo d'equilibrio ricevuto dai compratori - 10 in più del prezzo d'equilibrio
pagato ai venditori - e quindi 60.
Vediamo perciò che otteniamo lo stesso risultato finale qualunque prezzo usiamo come variabile sull'asse verticale dobbiamo solo essere accurati. L'effetto della tassa è di ridurre la quantità scambiata (in questo esempio da 45 a 40) e di
aumentare il prezzo pagato dagli acquirenti (in questo esempio da 55 a 60) e di decrescere il prezzo ricevuto dai
venditori (in questo esempio da 55 a 50). In questo esempio l'effetto è simmetrico - possiamo dire che la tassa è pagata
metà dagli acquirenti e metà dai venditori. Ma questa è una conseguenza delle particolari curve di offerta e di domanda
che abbiamo assunto - come vedremo.
Mettiamo tutti i grafici in una sola figura. Le curve sottili sono le curve di domanda e di offerta originali e quelle spesse
sono le curve nuove. E' chiaro quello che è accaduto: la tassa inserisce un cuneo tra domanda ed offerta e la quantità di
equilibrio nuova è dove c'è un a distanza verticale tra le curve di offerta e di domanda nuove pari alla tassa.
L'effetto della tassa sui surplus
Ora possiamo vedere quello che la tassa fa ai surplus - a quello totale e alla sua distribuzione. La posizione iniziale è
mostrata sotto. L'area blu è il surplus del compratore e l'area rossa il surplus del venditore.
Ricordatevi la situazione con la tassa - la figura 27.4 sopra ma con le curve originali spesse.
E' chiaro che possiamo liberarci delle nuove curve e ottenere una figura più chiara nella quale mostrare i nuovi surplus.
Il nuovo prezzo pagato dai compratori è 60, quindi il loro suplus è l'area blu nella figura 27.7. Il nuovo prezzo ricevuto
dai venditori è 50 quindi il loro surplus è l'area rossa nella figura 27.7.
L'area verde è il rendimento tale della tassa - pari alla tassa (per unità di bene) moltiplicato per il numero di unità
scambiate.
cosa cruciale - non soltanto i surplus del compratore e del venditore sono ridotti (a causa della tassa) ma esiste anche
una perdita di surplus che non è più generato dal mercato - il triangolo bianco nella figura. Questa è chiamata perdita
secca a causa della tassa . Ed è una perdita per la società - il mercato non genera più lo stesso surplus di prima, anche
contanto il surplus che ora affluisce al governo.
Fallimento del mercato
In economia, un fallimento del mercato è una situazione in cui i mercati non organizzano la produzione in maniera
efficiente, o non allocano efficientemente beni e servizi ai consumatori. Dal punto di vista degli economisti, il termine si
riferisce normalmente a situazioni in cui l'inefficienza risultante è notevole, o quando istituzioni esterne al mercato
potrebbero essere impiegate per raggiungere un risultato preferibile. Nel linguaggio di tutti i giorni, d'altra parte, il
termine è impropriamente utilizzato per designare le situazioni in cui le forze di mercato non appaiono servire ciò che è
percepito come interesse pubblico.
ASIMETRA INFORMATIVA
BENI PUBBLICI
IL POTERE DI MERCATO
Asimmetria informativa
Si è in presenza di asimmetria informativa quando l'intera informazione rilevante non è condivisa integralmente fra gli
individui facenti parte del processo economico, ovvero i casi in cui una parte degli agenti interessati ha maggiori
informazioni rispetto al resto dei partecipanti e può trarre un vantaggio da questa configurazione.
Il concetto viene usato e studiato in economia, dove si suppone la presenza di asimmetrie informative per spiegare i
differenti comportamenti dei soggetti economici.
La presenza di asimmetrie informative spiega per esempio perché i risparmiatori preferiscono ricorrere ai servizi di
investimento offerti dalle banche benché siano costosi.
Rispetto ai risparmiatori, le banche possiedono infatti informazioni migliori su un maggior numero di possibili
investimenti.
La minore conoscenza da parte del risparmiatore lo induce quindi a ricorrere a un operatore specializzato nella raccolta
e nell'elaborazione delle informazioni circa i possibili modi di investire il denaro.
Si possono presentare due distinti casi di asimmetria informativa:
•
•
Pre contrattuale selezione avversa (adverse selection)
Post contrattuale azzardo morale (moral hazard
Selezione avversa
Si ha il fenomeno della selezione avversa quando una sola delle parti coinvolte in un contratto dispone di
un'informazione e la usa a proprio vantaggio.
In questa situazione una delle due parti, normalmente detta principale, tende a selezionare la controparte del contratto,
detta agente, in modo controproducente. In altre parole, il contratto è conveniente solo per quegli agenti che hanno
caratteristiche inferiori alla media, mentre non lo è per quelli con caratteristiche superiori alla media. Di conseguenza i
primi stipulano il contratto e i secondi no. Il principale non seleziona quindi gli agenti migliori, ma quelli peggiori.
Un esempio
Nel caso delle macchine usate, il venditore conosce la reale qualità dell'auto che vende, mentre chi l'acquista, in base
alle statistiche, può essere al massimo a conoscenza della qualità media di una vettura di quella marca, quel modello, di
quella stessa età. Ciò fa sì che il prezzo dell'auto usata non ne rifletta effettivamente la qualità, ma si stabilisca attorno al
valore che ha la vettura media di quel tipo immatricolata in quel determinato anno. Gli effetti della selezione avversa sul
mercato non sono trascurabili. Un proprietario di auto di qualità superiore non troverà conveniente vendere a quel
prezzo, mentre chi possiede un'auto qualitativamente inferiore sarà invogliato a portarla sul mercato perchè ne riceverà
un prezzo superiore al valore effettivo. Di conseguenza la qualità media delle auto presenti sul mercato delle auto usate
tende ad abbassarsi, inducendo un ribasso dei relativi prezzi.
Azzardo morale
Il caso di azzardo morale è un caso che si verifica durante il rapporto assicurativo. Il consumatore, avendo stipulato un
contratto che lo tutela e lo risarcisce in caso di accadimento dell'evento negativo, è portato a non usare più strumenti e
accortezze cautelari che lo prevengano dall'evento. Il fatto di essere assicurato induce l'individuo a ridurre l'attività di
prevenzione o parallelamente a sovrautilizzare la disponibilità di risorse a lui dovute più di quanto non necessiti.
Beni pubblici
In economia, un bene pubblico è un bene che è difficile, o impossibile, produrre per trarne un profitto privato. Per
definizione, un bene pubblico è caratterizzato da:
Assenza di rivalità nel consumo - il consumo di un bene pubblico da parte di un individuo non implica l'impossibilità
per un altro individuo di consumarlo, allo stesso tempo (si pensi ad esempio a forme d'arte come la musica, o la pittura);
Non escludibilità nel consumo - una volta che il bene pubblico è prodotto, è difficile o impossibile impedirne la
fruizione da parte di consumatori (si pensi ad esempio all'illuminazione stradale).
Beni pubblici puri possiedono in senso assoluto tali proprietà. D'altra parte, poiché i beni pubblici puri sono rari
(sebbene includano importanti casi quali il sistema dei diritti di proprietà o la difesa nazionale), nel gergo degli
economisti il termine bene pubblico è in genere riferito a beni pubblici impuri, o pubblici soltanto con riferimento a un
particolare sottoinsieme di consumatori. È importante al riguardo osservare che un bene pubblico può essere fruito da
parte dell'intera società, laddove un bene che è utilizzato soltanto da un suo sottoinsieme dovrebbe essere considerato un
bene collettivo.
Un bene pubblico puro può essere inoltre definito in opposizione a un bene privato, ossia un bene caratterizzato da
rivalità nel consumo ed escludibilità. Una pagnotta è ad esempio un bene privato: il suo possessore può impedire ad altri
di consumarla, e una volta che essa è stata consumata, non può esserlo nuovamente.
Il libero mercato è in genere incapace di produrre un ammontare ottimale/efficiente (in senso paretiano) di beni
pubblici. Importanti beni, come il sistema dei diritti di proprietà, saranno "prodotti" in ammontare insufficiente, a causa
di problemi normalmente associati ai beni pubblici, quali il free riding. Nella pratica, tali difficoltà sono normalmente
affrontate e risolte tramite l'intervento dello Stato nell'economia. Questa soluzione non è tuttavia libera da critiche, in
quanto alcuni argomentano come possa condurre alla produzione/erogazione di beni pubblici in quantità eccessiva;
inoltre, una soluzione centralizzata che passi tramite l'intervento governativo non è l'unica possibile; almeno in via
teorica, soluzioni decentralizzate quali tradizione e democrazia possono svolgere un ruolo analogo.
Il concetto economico formale di bene pubblico non è, infine, da confondere con l'uso informale del termine, spesso
assimilato al pubblico interesse, che in generale rimanda a un giudizio di tipo etico, estraneo alla teoria economica dei
beni pubblici.
Il potere di mercato
Monopolio
Il monopolio è una forma di mercato dove un unico venditore offre un prodotto o un servizio per il quale non esistono
sostituti stretti.
In una economia così può venirsi a creare una situazione di monopolio:
• Esclusività sul controllo di input essenziali (es. diamanti grezzi de Beers);
• Economie di scala, laddove la curva del costo medio di lungo periodo è decrescente, ossia che un aumento
della produzione, "spalmando" i costi su più unità di prodotto, ne riduce l'incidenza media (questa condizione
può dare luogo a un monopolio naturale); un esempio è il (discusso) caso delle ferrovie;
• Brevetti;
• Licenze governative.
Forme di monopolio
I monopoli sono spesso caratterizzati in base alle circostanze da cui hanno origine. Tra le categorie principali si hanno
monopoli che sono il risultato di leggi o regolamentazione (monopoli legali), monopoli che hanno origine dalla struttura
dei costi di un dato sistema produttivo (monopolio naturale). I fautori del liberismo in economia sostengono che una
classificazione più fondamentale dovrebbe distinguere tra monopoli che nascono e prosperano grazie a una violazione
dei principî del libero mercato (monopolio coercitivo) e quelli che si mantengono tali grazie alla superiorità del prodotto
o servizio offerto rispetto a quello dei potenziali concorrenti.
L'oligopolio
L'oligopolio è una forma di mercato con pochi ma importanti venditori (offerenti), ognuno dei quali sa che ogni sua
decisione avrà influsso sulle decisioni della concorrenza.
Un esempio di oligopolio viene, ad esempio, dall'industria automobilistica.
Il Duopolio è - per contro - un oligopolio con soli due offerenti.
Teoria dei giochi
La Teoria dei giochi è la scienza matematica che analizza situazioni di conflitto e ne ricerca soluzioni competitive e
cooperative tramite modelli, ovvero uno studio delle decisioni individuali in situazioni in cui vi sono interazioni tra i
diversi soggetti, tali per cui le decisioni di un soggetto possono influire sui risultati conseguibili da parte di un rivale,
secondo un meccanismo di retroazione.
Le applicazioni e le interazioni della teoria sono molteplici: dal campo economico e finanziario a quello strategicomilitare, dalla politica alla sociologia, dalla psicologia all'informatica, dalla biologia allo sport, introducendo l'azione
del caso, connessa con le possibili scelte che gli individui hanno a disposizione per raggiungere determinati obiettivi,
che posso essere:
comuni
comuni, ma non identici
differenti
contrastanti.
Possono essere presenti anche aspetti aleatori.
Nel modello della "Teoria dei Giochi", tutti devono essere a conoscenza delle regole del gioco, ed essere consapevoli
delle conseguenze di ogni singola mossa. La mossa, o l'insieme delle mosse, che un individuo intende fare viene
chiamata "strategia". In dipendenza dalle strategie adottate da tutti i giocatori (o agenti), ognuno riceve un "pay-off"
(letteralmente il "pagamento d'uscita", o meglio la vincita finale) secondo un'adeguata unità di misura, che può essere
positivo, negativo o nullo. Un gioco si dice "a somma costante" se per ogni vincita di un giocatore v’è una
corrispondente perdita per altri. In particolare, un gioco "a somma zero" fra due giocatori rappresenta la situazione in
cui il pagamento viene corrisposto da un giocatore all'altro. La strategia da seguire è strettamente determinata, se ne
esiste una che è soddisfacente per tutti i giocatori; altrimenti è necessario calcolare e rendere massima la speranza
matematica del giocatore, che si ottiene moltiplicando i compensi possibili (sia positivi sia negativi) per le loro
probabilità.
Tipologia di giochi
I giochi possono essere classificati in base a diversi paradigmi:
•
Cooperazione
•
Giochi non cooperativi
Se i giocatori perseguono un fine comune, almeno per la durata del gioco, alcuni di essi possono tendere ad associarsi
per migliorare il proprio "pay-off". La garanzia è data dagli accordi vincolanti.
Si posso avere due sottogeneri, i giochi NTU ed i giochi TU.
Giochi NTU
"Non Transferable Unit": a utilità non trasferibile o senza pagamenti laterali. In questi casi, nel campo dell'economia
industriale, in una situazione di oligopolio può insorgere il fenomeno della
Giochi TU
"Transferable Unit": a utilità trasferibile o con pagamenti laterali, nei quali deve esistere un mezzo, denaro o altro, per il
trasferimento dell'utilità.
La suddivisione della vincita avviene in relazione al ruolo svolto da ciascun giocatore, secondo la sua strategia ed i suoi
accordi (per i "giochi TU" vanno aggiunti i pagamenti o i trasferimenti ottenuti durante il gioco).
I giocatori non possono stipulare accordi vincolanti (anche normativamente), indipendentemente dai loro obiettivi. A
questa categoria risponde la soluzione data da John Nash con il suo Equilibrio di Nash, probabilmente la nozione più
famosa per quel che riguarda l'intera teoria, grazie al suo vastissimo campo di applicabilità.
Equilibrio di Nash
La prima formulazione di questo teorema, che costituisce la nozione di equilibrio più famosa della teoria dei giochi per
quel che riguarda i "giochi non cooperativi", appare in un brevissimo articolo del 1949 dove John Nash, ancora studente
a Princeton, spiega la sua idea di fondere intimamente due concetti apparentemente assai lontani: quella di un punto
fisso in una trasformazione di coordinate, e quella della strategia più razionale che un giocatore può adottare, quando
compete con un avversario anch'esso razionale, estendendo la teoria dei giochi ad un numero arbitrario di partecipanti, o
agenti, e dimostrando che, sotto certe condizioni, esiste sempre una situazione di equilibrio, che si ottiene quando
ciascun individuo che partecipa a un dato gioco sceglie la sua mossa strategica in modo da massimizzare la sua funzione
di retribuzione, sotto la congettura che il comportamento dei rivali non varierà a motivo della sua scelta (vuol dire che
anche conoscendo la mossa dell'avversario, il giocatore non farebbe una mossa diversa da quella che ha deciso).
Tutti i giocatori, possono dunque operare una scelta dalla quale tutti traggono un vantaggio (o limitare lo svantaggio al
minimo). Una differenza sostanziale rispetto al caso dei giochi a "somma zero" studiati in precedenza da John von
Neumann, dove la vittoria di uno dei due (unici) partecipanti era totale e necessariamente accompagnata dalla sconfitta
all'altro.
•
Rappresentazione
Giochi ad informazione perfetta, giochi in cui, in ogni momento, si conosce con certezza la storia delle giocate
precedenti. In termini più tecnici, si tratta di giochi in cui in ogni momento del gioco si può capire in quale nodo della
rappresentazione ad albero del gioco (rappresentazione estesa) ci si trova. (esempio gli scacchi)
•
Numero di giochi
Giochi finiti, giochi in cui il numero delle situazioni di gioco possibili è finito. (esempio il tris)
•
Somma
Giochi a somma zero in cui la somma delle vincite dei due contendenti in funzione delle strategie utilizzate è sempre
zero. Negli scacchi ad esempio significa che i soli tre risultati possibili, rappresentando la vincita con 1 la perdita con -1
e il pareggio con zero possono essere (1,-1), vince il bianco, (-1,1) vince il nero, (0,0) pareggiano. Non esiste ad
esempio il caso in cui vincono entrambi o perdono entrambi.
Giochi a somma non zero in cui la somma di cui al punto precedente non è zero almeno in un caso.
L’impresa nel breve periodo
Ipotesi isoquanto convesso
( )
Qb = Q K , L
I)
Qa
Tgα
produttività media
λ
La
dQ
in a
produttività marginale
Tgβ =
λ'
dL
Il punto B (flesso) è il punto di massimo per λ '
Fino al punto B la produttività marginale è maggiore della produttività media, nel punto C le due
produttività sono uguali, Dopo il punto C, la produttività media è maggiore della produttività
marginale.Tutto ciò significa che assumere lavoratori il prodotto marginale è crescente dopodiché
diminuisce…
II)
Il punto C è il punto di massimo rendimento per l’impresa
Costi dell’impresa
C t = C f + C v (costo totale = costi fissi + costi variabili)
C f = C k , C h ( C k costo capitale, C h costo gestionale )
C v = C mp + C mdo (costo materie prime + costo manodopera)
ciò che è rilevante è C mdo
C v = WxL (salario unitario x lavoratori)
Q
Q
quindi
sappiamo che λ =
allora L =
L
λ
Q
C v = Wx questa relazione dice che esiste un rapporto inverso tra costi variabili e produttività
λ
III)
IV)
Tgα
C va
Qva
costo medio
Tgβ =
dC
dQ
costo marginale
V)
Il punto P, è un punto di uscita dal mercato, perché al di sotto del punto X
Sotto il punto PX c’è l’uscita dal mercato
L’area compresa tra X e J, rappresenta “l’uscita nel breve periodo”
Dal punto J in su si realizzano gli extraprofitti
In concorrenza perfetta il punto J è il punto di equilibrio
Concorrenza = prodotto omogeneo, grande numero di imprese, assenza di barriere di ingresso
Ipotesi isoquanto a coefficienti fissi
Lungo periodo
Tratto 1 = impresa con un certo tipo di tecnologia
Tratto 2 = stessa impresa con tecnologia meno efficiente del tratto 1
Tratto 3 = stessa impresa con tecnologia meno efficiente del tratto 2