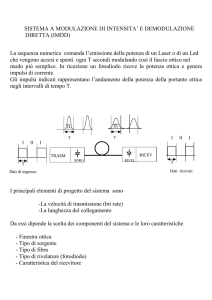
Coefficiente di estinzione di un mezzo torbido
Impostazione della misura
sorgente di luce
collimata
Pe
mezzo
torbido
P0
misuratore di
potenza
Fig. 1- Schema a blocchi dell’apparato di misura
La sorgente di luce è un Laser a semiconduttore di potenza luminosa ≈ 5 mW( 1). La
sua luce rossa, collimata e monocromatica (0.635 µm), illumina un fotodiodo (2) che, posto di
fronte a circa 10 cm, misura la potenza luminosa incidente.
Fra Laser e fotodiodo è interposta una vaschetta di vetro (cella) da ≈150 mL. Nella
cella sono immessi 100 mL di acqua e in passi successivi (≈7 in totale), una determinata
quantità di inchiostro nero di china.
La soluzione acqua-china così prodotta è il “mezzo torbido” che attenua il fascio laser.
Un pò di teoria.
Un fascio di luce collimato e monocromatico che si propaga in un mezzo torbido omogeneo
si attenua secondo la legge
P( z ) = P e e − µext z 1)
Pe è la potenza luminosa all’ingresso del mezzo e z è la profondità alla quale il fascio arriva
con potenza inferiore P(z). µext è il “coefficiente di estinzione” e le sue dimensioni sono [L-1]
perché il prodotto µext z è adimensionale (3).
La legge è detta di Lambert-Beer o semplicemente di Beer o più raramente di BouguerLambert-Beer. I tre nomi descrivono il percorso di più di un secolo della 1) che parte dalla
prima metà del ‘700 con il francese Pierre Bouger per arrivare a metà ‘800 col tedesco
August Beer.
1
Electron LQB
2
CENTRONIC - OSD5-5T
3
Se il fascio fosse fortemente divergente e/o non monocromatico la 1) dovrebbe essere riscritta in
forma assai più complicata. Nel caso di forte divergenza dei raggi luminosi i percorsi nel mezzo
torbido non sarebbero più uguali e non potrebbero essere più descritti da un unico valore z. Analoga
cosa per il coefficiente di estinzione µext nel caso di luce non monocromatica in quanto esso dipende
dal colore della radiazione (lunghezza d’onda).
1/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Le cause fisiche dell’estinzione sono riconducibili a due fenomeni distinti,
l’assorbimento e la riflessione (“scattering”) da parte delle molecole o particelle del mezzo
attraversato. Scattering e assorbimento determinano la torbidità del mezzo. Una descrizione
piana degli effetti citati si trova nella nota acclusa “Propagazione di radiazione luminosa in
mezzi naturali”.
All’uscita dal mezzo di spessore d, la potenza luminosa del fascio è ridotta a
P0 = P ( z = d ) = P e e − µext d
dalla quale si ricava il coefficiente di estinzione
P
1
µ ext = log e ( e ) d
P0
2)
Nel caso µext d =1, Po = Pe/e con e numero di Eulero ( 4) (e ≈ 2.718 281 828....). Questa
osservazione sarà richiamata più oltre.
Il prodotto (d µext) è detto anche “assorbanza”, sebbene a volte sia definito tramite il
logaritmo in base dieci al posto di quello in base e che compare nella 2) (5).
L’attenuazione complessiva (vedi nota citata) è riconducibile alla somma delle
attenuazioni che ciascuno dei “tantissimi volumetti ideali” di liquido attraversati dal fascio
opera indipendentemente l’uno dall’altro. Pensando alla luce in termini di fotoni e al fascio di
luce come a un getto di fotoni, possiamo dire che ciascun volumetto ha una determinata
probabilità di assorbire/deviare un fotone. Quindi quello che osserviamo all’uscita è dovuto
alla probabilità complessiva che ciascun fotone ha di uscire “indenne” dall’attraversamento
della successione dei volumetti e quindi dal mezzo torbido. Su questo aspetto tornerò nella
seconda parte delle nostre attività.
4
Matematico svizzero (1707-1783)
5
Definizioni di logaritmo “naturale” (base e) e logaritmo in base 10 : e
log e x
= x,
10
log10 y
A volte log10 y è scritto come Log y, ma c’e` un po’ di confusione e occorre stare attenti.
2/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
= y
Descrizione del dispositivo sperimentale e obiettivo della misura.
In Fig. 2, Fig.3 le parti salienti del dispositivo in accordo allo schema a blocchi di Fig.
1. In entrambe si evidenzia l’assottigliamento e la perdita di luminosità del fascio laser nello
attraversare la soluzione acqua-nero di china. Entrambi gli effetti sono riconducibili alla 1).
Fig.2 - La cella di vetro (8x4x6 cm3, spessore pareti 4 mm) è riempita con 100 mL di soluzione acqua-nero di
china. Il fascio, proveniente dal laser (colonnino a sinistra), attraversa la soluzione per incidere sul diodo posto
sul supporto al di là della cella.
cella di vetro
3 cm
fotodiodo
fascio laser
Laser
(0.635 µm)
Fig. 3- Vista dall’alto dell’attraversamento della cella riempita colla soluzione assorbente da parte del fascetto
rosso del Laser. La parte emergente raggiunge il fotodiodo che ne misura la potenza.
Nel suo cammino il fascio laser attraversa ≈ 3 cm di liquido (dl) più ≈ 8 mm di vetro (dvetro).
Per la 1) si può scrivere
PO = Pe × e
−µvetro dvetro
× e
−µ mt dliquido
3)
3/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
P0 è misurata dal fotodiodo. Pe, potenza emessa dal laser, non è misurata e assumiamo che
rimanga costante durante tutta la misura.
La quantità µ vetro dvetro è costante, µ mt dl invece dipende, tramite µext dalla quantità di
inchiostro che immettiamo nell’acqua (concentrazione). µmt è il coefficiente di estinzione del
mezzo torbido (acqua e china nera).
Scopo delle misure è quello di verificare che µ mt dl dipende in modo lineare dalla
concentrazione di inchiostro, che noi misureremo in termini di “numero di gocce” (Ngi)
immesse nell’acqua. Le gocce sono prodotte con una siringa da 2.5 mL, che, se maneggiata
con un minimo di accorgimento, consente una buona riproducibilità, entro il ±2%.
All’inizio della procedura la cella di vetro è riempita con 100 mL di acqua. Così facendo
vogliamo verificare che
µ
d
= α N + β
mt liquido
gi
4)
con α costante che dipende dallo spessore di liquido attraversato e dalla natura
dell’inchiostro, e β dallo spessore e dalle caratteristiche fisiche dell’acqua .
Il modo di verificare la 4) è misurare PO in corrispondenza dei vari Ngi.
Per la 3) ci aspettiamo
PO = Pe × e
−µvetro dvetro
×e
−α N gi + β
−α N gi
= Pe × A × e
5)
e quindi dobbiamo verificare se le misure della potenza emergente PO varino con Ngi in modo
esponenziale. Una verifica molto tradizionale e semi quantitativa è quella di riportare in un
grafico semi logaritmico i valori di P (ordinate) vs Ngi (ascisse) e giudicarne il
comportamento rettilineo in rapporto alle stime fatte sugli errori delle misure. Per questa
verifica la conoscenza delle costanti moltiplicative della 5) non ha importanza.
In Fig.4 sono presentati i circuiti di polarizzazione del diodo laser e del fotodiodo
utilizzati nel dispositivo del laboratorio. Entrambi sono alimentati dallo stesso generatore
L’intensità di luce emessa dal laser è proporzionale alla corrente isegnale ( Pe ∝ ilaser ) e la
corrente isegnale che scorre sul fotodiodo e sulla sua resistenza serie Rs è proporzionale a P0
( isegnale ∝ P0 ). Questo assicura che ∆Vs = Rs isegnale = k P0 con k costante di
proporzionalità che dipende dal fotodiodo e dalla sua resistenza serie. In sintesi
4/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
isegnale < 5 µA
Rp = 180 Ω
Rs = 1 MΩ
9÷10 V
∆Vs = Rs isegnale
Fig. 4 - Circuito per la misura della trasmissione di luce attraverso un liquido torbido. Rp è la resistenza di
polarizzazione del diodo Laser, Rs quella del fotodiodo. Il laser è polarizzato direttamente, il fotodiodo
inversamente. isegnale e ∆Vs sono determinati dalla potenza luminosa incidente sul fotodiodo.
I due valori per il generatore di tensione si riferiscono ai due tipi di dispositivi a disposizione in lab.
∆ Vs = k × P × A × e
e
−α N
gi
5’)
Noi misureremo la d.d.p. ∆Vs per ciascun numero di gocce immesse nell’acqua.
Le nostre correnti di segnale partono da circa 5 µA (6) con l’acqua ancora pura e scendono di
un paio di decadi con l’immissione di una sessantina di gocce d’inchiostro. Assumendo che
circa ogni due fotoni incidenti sul fotodiodo si liberi un elettrone il flusso di fotoni che incide
sul fotodiodo durante le misure è ≤ 2x10 13 fotoni/s.
In Fig. 5 dispositivo e apparecchiatura di supporto per la misura.
6
1 µA = 1x10-6 A. Poiché la carica di un elettrone ≈ 1.6x10-19 C, 1 µA ≈ 6 x1012 elettroni/s
5/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
gneratore di
tensione DC
BNC banane
(uscita fotodiodo)
Fig. 5- Sistema per la misura del coefficiente di estinzione di una soluzione acqua china nera. La parte
corrispondente al circuito a blocchi di Fig. 4 è contenuta nella scatola scoperchiata con frontalino grigio. Al suo
interno è visibile la vaschetta di vetro con il bastoncino per agitare la miscela prima della misura. Per accendere
i circuiti elettrici inserire il generatore di tensione DC nella presa di rete come si fa con un qualsiasi ricarica
batterie. Sulla destra il flacone con l’inchiostro e la siringa da 2.5 mL. Tester e Oscilloscopio sono quelli
illustrati a lezione (Allalavagna).
6/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Osservazioni
Nei limiti della stabilità del laser e dell’alimentazione (generatore di tensione da
9÷10V), correnti e tensioni sono da ritenersi in continua.
Fig.6 - L’oscilloscopio è connesso tramite la sonda all’uscita del fotodiodo
☞ Invito tuttavia ad osservare all’oscilloscopio (utilizzare la sonda x10 ), l’uscita del
fotodiodo come mostrato in Fig. 6.
Fissate l’asse dei tempi a 5 ms/Div e selezionate Menù Trigger >> Source>>AC Line.
Ponendo il canale d’ingresso in AC e scegliendo per esso una scala verticale adeguata
(≈50 mV/div) risulta ben visibile l’andamento seghettato della traccia dell’oscilloscopio.
Ponete adesso l’ingresso in DC e abbassate la sensibilità del canale (≈1V/div) per
mantenere visibile la traccia sullo schermo. L’andamento periodico seghettato appare
adesso molto piccolo e corre su un valore medio di tensione che, è facile verificare, è
quello misurato dal tester (≤ 5 V, a secondo della scatola in dotazione). Questo perché il
tester in DCV fa una media temporale del segnale in ingresso su un tempo lungo rispetto
al suo periodo. La ragione della forma seghettata è l’alimentazione del circuito laser che,
ricavata dall’alternata di rete, non è esattamente costante come quella di una pila e quindi
anche l’intensità del laser ne risulta modulata.
7/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
☞ ☞ Fatta questa osservazione, riportiamo l’ingresso in AC e selezioniamo la sensibilità
massima compatibile con lo schermo per misurate ampiezza e periodo della forma
seghettata coi cursori dell’oscilloscopio (pigiare il pulsante Cursors per attivarli). Per il
periodo troverete 10 ms, uguale a metà del periodo della tensione di rete.
Sorge la domanda. Le misure di ∆Vs per la verifica della 5) sono fatte col tester in
posizione DCV (corrente continua), l’effetto messo in evidenza può influenzarle? La
risposta è no perché l’attenuazione del fascio non dipende dalla sua intensità iniziale eppoi
il tester in DCV “media” su tempi lunghi rispetto al periodo di 10 ms.
☞ ☞ ☞ Con il canale dell’oscilloscopio in posizione DC, si osservi la traccia
dell’oscilloscopio quando nella vaschetta si agita un bastoncino. Si nota un pronto e netto
abbassamento della tensione al passaggio di questo attraverso il fascetto laser. L’ombra del
bacchetto oscura, durante il suo passaggio, il fotodiodo provocandone l’abbassamento
della corrente isegnale.
☞☞☞☞
Un’ultima osservazione, di carattere strumentale per capire l’influenza che in
generale hanno le resistenze d’ingresso degli strumenti di misura sulla misura stessa.
Fig.7 - L’uscita del fotodiodo è connessa al Tester e all’oscilloscopio una volta con la sonda X10 e una X1
(inserto).
Inserire le banane del raccordo BNC nel tester in posizione DCV. A lettura fatta, contattare
i due ingressi del multimetro con la sonda X10 connessa al canale dell’oscilloscopio posto
in DC. Osserverete un abbassamento del valore della d.d.p. Questo abbassamento è ancora
8/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
più appariscente se commutiamo la sonda da X10 a X1. In Fig. 7 è riportato il confronto
fra i due casi( 7).
Con l’aiuto dello schema di Fig. 8 giustificare i valori di tensione osservati nei tre casi:
solo tester, tester+sonda X10, tester+sonda X1.
dispositivo Lab
isegnale
Rp =9MΩ
RinO = 1 MΩ
RinM = 10 MΩ
oscilloscopio
Rs =1MΩ
BNC
multimetro
Fig. 8 - La corrente isegnale del fotodiodo si ripartisce fra la resistenza Rs e le resistenze ad essa in parallelo. RinM
è la resistenza interna del multimetro, Rp + RinO e RinO le resistenze dell’oscilloscopio+ sonda con X10 e
oscilloscopio+ sonda con X1. Le connessioni dall’oscilloscopio al BNC mostrate sono dovute alla sonda. In
figura è mostrata la sonda X10. Ricordare che nel caso X1, Rp = 0.
☞ ☞ ☞ ☞ ☞ Dopo l’immissione dei 100 mL di acqua nella cella di vetro (vedi “Misure”,
pag. 10) e utilizzando il solo tester in DCV, si osserva che ∆Vs varia in modo irregolare
entro un certo intervallo di valori. Prolungando l’osservazione per un paio di minuti,
stimare l’intervallo di variazione e valutare il valore più frequentemente assunto da ∆Vs.
Riportare questi valori nelle colonne di Tab I (vedi “Misure”, pag. 12), utilizzando solo le
tre cifre più significative.
La ragione delle instabilità è dovuta quasi esclusivamente al laser, il cui funzionamento
può avere qualche criticità nei dispositivi commerciali a basso costo come quelli qui
utilizzati.
Data la bassa frequenza delle instabilità (≤ 1Hz) la media temporale fatta dal tester non
riesce ad eliminarle. Potremmo ricorrere ad alcuni accorgimenti ma la semplicità del
sistema a disposizione non lo consente e quindi con un pò di perizia individuale dobbiamo
valutare media e scarto massimo per avere un’idea delle incertezze coinvolte
nell’osservazione del fenomeno.
7
Attenzione : i valori mostrati nelle foto di Fig.7 si riferisco ai vecchi dispositivi diversi da quelli ora in uso. In
lab non troveremo mai una risposta del fotodiodo a 8.13V.
9/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Misure
Fig. 9 - Misure di attenuazione: solo il tester in DCV.
La misura della d.d.p ai capi della resistenza da 1 MΩ fatta col solo tester di
resistenza interna 10 MΩ (Fig.8) comporta l’attenuazione della d.d.p. di circa il 10%, in
quanto isegnale si ripartisce fra resistenza Rs e resistenza RinM del multimetro. Applicando la
regola di somma delle resistenze in parallelo si trova che la resistenza complessiva vale
≈0.91MΩ e quindi le tensioni misurate sono più piccole della stessa entità.
Questo non inficia la nostra verifica, apporta semplicemente una modifica al fattore
moltiplicativo della 5’)
−α N
gi
∆ Vs = 0.91 × k × P × A × e
e
In Tab. I l’ organizzazione dei dati per la verifica della 5”) e quindi della 4).
5”)
Ad ogni passo, corrispondente all’immissione del numero di gocce indicato, riportare la stima
dell’incertezza sul volume d’inchiostro, il valore ∆Vs letto, espresso in volt, e l’incertezza
sulla misura (u), sempre espressa in volt.
Il primo passo corrisponde alla vaschetta con sola acqua (100 mL). Il riempimento
avviene mediante siringa graduata da 60 cc.
In ciascuno dei passi successivi, nella cella si aggiungono 10 gocce di inchiostro
mediante la siringa da 2.5 mL in dotazione. Con un pò di attenzione, si assume di riprodurre
le gocce entro il 2% (volume). Dal punto di vista delle elaborazioni dei dati quindi è come se
il numero di gocce fosse affetto dal ±2% di incertezza massima. Data l’importanza è bene
10/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
“farsi la mano” prima di iniziare a immettere gocce nella cella. Ricordarsi di controllare
riempimento e inclinazione della siringa, spinta sullo stantuffo.
Con la sola acqua nella cella la risposta del fotodiodo, misurata dal tester, varia da
≈3V a ≈5V a seconda del dispositivo in uso. Per questo motivo all’inizio delle misure va
annotato il numero riportato sul frontale del dispositivo. In tutti i casi, all’inizio, è necessario
l’utilizzo del fondo scala 20V del multimetro in posizione DCV. Nell’intorbidire la soluzione
acquosa, la risposta del fotodiodo diminuisce e sotto i 2V è conveniente usare il fondo scala
2V fino a che i segnali scendano sotto ai 200mV nel qual caso si passa al fondo scala 200mV.
Tutte le volte che si aggiungono nuove gocce, agitare il liquido della vaschetta per
rendere la soluzione omogenea ed attendere uno due minuti affinché tutto si stabilizzi. Anche
le turbolenze possono contribuire alle instabilità del segnale.
È utile precauzione, durante la misura di ∆Vs, tenere la scatola chiusa per evitare che
il fotodiodo senta la luce ambiente. Questa precauzione può essere importante negli ultimi
passi, quando il fascio laser è fortemente attenuato e la risposta del fotodiodo sotto i 200 mV.
Tab.I - La seconda colonna è la stima dell’errore (2%) sul volume delle Ngi gocce di inchiostro. La quarta (u /
V ) è quella sull’errore massimo atteso in base alle formule sull’accuratezza del tester e alla instabilità del
segnale (vedi testo). ∆Vs è il segnale di tensione oggetto della misura.
Il cambio del Fondo Scala a 20 e a 50 è indicativo in quanto dipende da dispositivo e qualità dell’inchiostro.
num.dispositivo..... è il numero scritto sul pannello frontale. Data..... è la data del giorno della misura.
num. dispositivo : ...................
Gocce
0.02 x
Inchiostro
Ngi
(Ngi)
0
∆Vs /V
Data......................
u /V
TESTER
Fondo accuratezza
Scala
/V
/V
20
±( 0.7% ∆Vs
+ 0.05 )
2
±( 0.7% ∆Vs
+ 0.005 )
utester
/V
(∆Vsmax-min)*0.5
/V
10
20
30
40
50
0.2
±( 0.5% ∆Vs
+ 0.0005 )
60
70
11/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Come visto nel caso di sola acqua, ∆Vs mostra oscillazioni a bassa frequenza e
apparentemente irregolari anche dopo qualche minuto dal mescolamento della soluzione.
Pertanto riportare nella terza colonna (∆Vs) della tabella il valore più frequente osservato e
nell’ultima, (∆Vsmax-min)*0.5, metà della differenza fra i valori estremi entro i quali esso
oscilla utilizzando le tre cifre più significative.
utester è l’incertezza massima attesa in base alle caratteristiche date dal costruttore, si
ricava dalle formule della colonna “accuratezza”.
Nella colonna dell’incertezza complessiva u delle misure inserire il valore massimo di
volta in volta fra utester e (∆Vsmax-min)*0.5.
12/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Verifiche
La procedura standard tradizionale per la verifica, un pò qualitativa, dell’ipotesi 4) è
quella di riportare i dati su un grafico ove l’asse delle ascisse è in scala lineare e quello delle
ordinate in scala Log (base 10) (grafico semi logaritmico, vedi Nota 3). In ascisse si riporta il
numero delle gocce e in ordinate le tensioni misurate.
Fig.10- Carta semi logaritmica a tre decadi. In ciascuna decade sono riportate le posizioni dei decimi relativi.
L’ascissa è divisa in dieci intervalli (≈ 1cm) a sua volta divisi in dieci parti
13/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Il motivo di questa procedura è dato dall’osservare che per la 5”) o 5’) Log (∆ Vs ) = −α N + Log 0.91 × k × P × A
gi
e
(
)
ossia i logaritmi delle tensioni misurate sono proporzionali al numero di gocce d’inchiostro.
Riportando sulla carta di Fig.8 i punti sperimentali della tabella possiamo giudicare se entro
le incertezze, “sono compatibili” con una retta. Non ci aspettiamo che tutti i punti delle
misure siano “esattamente” allineati, ci aspettiamo che lo siano entro i “limiti delle
incertezze” massime valutate.
Non di rado succede che la linearità sul grafico non sia ben verificata anche per la cattiva
uniformità delle gocce (ben superiore al 2%). Questo giusto per esortare a un pò di attenzione
nel produrle con la siringa. È tuttavia da sottolineare che la stima del 2% riguarda la misura
fatta da un gruppo che lavori in modo accurato. Ma a parità di accuratezza la differenza fra
gruppi diversi può essere superiore in quanto il volume delle gocce dipende anche dal modo
con cui si decide di operare. Questa circostanza influisce sulla confrontabilità delle misure dei
vari gruppi non sulla verifica dell’andamento esponenziale dell’attenuazione.
Prima di riportare i valori sulla carta di Fig.10 in ordinate assegniamo i valori alle tre
decadi a partire dal limite inferiore della più bassa (0.01V) fino ai 10 V del limite superiore
della più alta. In ascisse segniamo 10 gocce/div a partire da zero.
Le incertezze sono disegnate con segmenti di ampiezza pari al loro valore con la loro
estremità nel punto della misura. Se i segmenti sono troppo piccoli per essere disegnati, in
margine al grafico si scriva che gli errori rientrano nella risoluzione grafica del disegno.
Con un righello tracciamo la retta che meglio approssima l’andamento complessivo ed
esprimiamo un giudizio di merito.
Sul grafico semi log è possibile dare una stima del coefficiente α ricordando che (vedi 5”))
per α Ngi = 1 l’intensità decresce del fattore 1/e. Specificarne valore e unità di misura.
======
14/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Sul quaderno
Introdurre il programma di misure riportando succintamente la loro ragione.
Richiamare per questo le equazioni 1), 3), 4), 5”) e riportare il disegno di figura 8 omettendo
le connessioni con l’oscilloscopio.
Riassumere il protocollo delle misure.
Riportare le misure fatte e le informazioni richieste secondo la Tabella I
Accludere (incollare) il grafico, in carta semilog, dei dati corredati degli errori ed esprimere
un parere sull’attendibilità della 4) e 5’) o 5”). Riportare la stima fatta di α.
Ad elaborazione grafica avvenuta accludere tabella e grafici ottenuti col programma
Kaleidagraph
15/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
C
Nota 3 - Presentazione grafica delle regressioni fra due grandezze
20
Nome Variabile Dipendente ( Unita' di misura )
15
10
5
0
0
2
4
6
8
10
nome variabile indipendente ( Unita' di Misura )
12
14
Fig.1 - Foglio prestampato di “carta millimetrata” ( 90% del formato A4) con quadrettatura
principale da 1 x 1 cm2 , suddivisa in una da 1 x 1 mm2 . Su di esso è riportato l’andamento
di alcuni dati sperimentali. L’andamento aspettato è di tipo esponenziale. Notare le barre di
“errore”(solo asse Y).
16/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Per riportare in grafico un gruppo di coppie di misure di grandezze correlate
occorre stabilire le scale (Unità di misura/cm) e il loro zero.
Le scelte sono fatte in base agli intervalli di distribuzione delle misure e alle dimensioni del
foglio a disposizione.
Assieme ai punti di misura è corretto riportare (è richiesto) le incertezze di misura sotto
forma di doppia barra, una ascendente e una discendente. L’ampiezza di ciascuna barra è
quella dell’incertezza in accordo alla scala prescelta. In Fig.1 sono evidenziate solo le barre di
errore della grandezza riportata in Y, ma in generale può essere necessario fare altrettanto per
quella sull’asse delle X.
In assenza delle barre di errore va esplicitamente dichiarata la circostanza. Può anche
succedere che l’ampiezza delle barre di errore sia entro la risoluzione grafica del disegno e
quindi sia impossibile disegnarle, va appunto dichiarato.
Esistono carte “semilog” come mostrato in Fig. 2. Le ascisse sono ancora suddivise in
centimetri e millimetri come nella carta millimetrata normale. Le ordinate sono suddivise
secondo il logaritmo in base dieci dei numeri del tipo n x 10 m con n numero naturale e m
intero. Partiamo da n = 1 e m = 0 (Log 1 = 0) la sua posizione sulla scala delle Y è dove
decidiamo di porre lo zero. Passiamo a n = 1, m = 1 (Log10 =1), la sua posizione sulle Y è
più sopra, ad una distanza pari all’unità grafica scelta per disegnare la carta. Per n = 1, m = 2
( Log100 = 2 ) la posizione è due unità più sopra. Se consideriamo invece n = 1, m = -1 (Log
0.1 = -1) la sua posizione è un’unità grafica più sotto lo zero e così via.
L’unità grafica, corrispondente alla variazione di un fattore dieci dei numeri da rappresentare
(decade), può essere scelta a piacere (5 cm in Fig. 2). I sottointervalli marcati in ciascuna
decade corrispondono ai numeri interi in essa compresi. Al di sopra di 1 si trova 2, 3, 4,....fino
a 9. Oltrepassato 10 si riparte con 2 x10, 3 x10,… Scendendo sotto 1 si trova 9 x0.1, 8
x0.1,....
fino a 0.2 da dove, passato 0.1, si riparte con 9x0.01, 8 x0.01,…
Riportare in ordinate i valori di Y con la scala descritta significa graficare “LogY” e quindi se
la sua dipendenza da X è esponenziale, è ovvio che il grafico abbia andamento lineare. In
Figura 2 la linearità è buona per X < 6 (Unità di Misura). A valori superiori l’andamento
appare mascherato dagli errori percentualmente rilevanti.
17/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
La carta semilog è un vecchio artificio che permette di capire rapidamente se i dati
sperimentali hanno un andamento compatibile con un esponenziale o no. In assenza di
computer può essere molto utile.
Esistono anche carte Log-Log ove entrambe le scale, l’orizzontale e la verticale,
hanno scala logaritmica. L’utilizzo di queste carte permette di individuare regressioni tipo Y
≈ X a con a qualsiasi. Si ha infatti che LogY ≈ a LogX e quindi adoperando scale doppio
logaritmiche si ha ancora una retta !
Segnalo l’utile sito web dal quale scaricare gratis (in formato A4 o altri) carte
millimetrate lineari, carte Log-Log o semilog, e altre ancora.
http://www.pdfpad.com/graphpaper/
18/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
100
Nome Variabile Dipendente ( Unita' di misura )
10
1
0.1
0.01
0
2
4
6
8
10
nome variabile indipendente ( Unita' di Misura )
12
14
Fig. 2 - Foglio prestampato di “carta semilog” (90% del formato A4). L’asse orizzontale è
suddiviso in millimetri e centimetri. Quello verticale secondo il logaritmo in base dieci dei
numeri da 1 x 10 -2 a 1x 102. Su di esso sono riportati i dati sperimentali di Fig.1 con le loro
barre di “errore” ( solo asse Y).
19/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Appendice
PROPAGAZIONE DI RADIAZIONE LUMINOSA IN MEZZI NATURALI
Giovanni Zaccanti
Dipartimento di Fisica dell’Università di Firenze
Propagazione nel vuoto: nel vuoto un raggio di luce (fascio di luce collimata, es. fascio
laser) si propaga indefinitamente in linea retta
Propagazione nei mezzi naturali: le variazioni spaziali dell’indice di rifrazione, n,
provocano deviazioni nella direzione di propagazione. In presenza di discontinuità nell’indice
di rifrazione si può avere riflessione e rifrazione oppure scattering.
Riflessione e rifrazione
Si ha se la superficie di separazione fra i due mezzi con diverso indice di rifrazione è liscia,
ovvero se la rugosità della superficie di separazione è piccola e il raggio di curvatura è molto
grande rispetto alla lunghezza d’onda della radiazione (es. lastra di vetro, di plexiglass,
superficie di un liquido in quiete, ecc). In questo caso il fascio di radiazione si divide in due
parti lungo direzioni ben precise. Il fenomeno è descritto dalla legge di Snell e dal
coefficiente di riflessione di Fresnel: la legge di Snell (ricordata in Fig. 1) ci dice quali sono
le direzioni di propagazione dei raggi riflesso e rifratto; il coefficiente di riflessione di Fresnel
R (θ i )
(del quale è riportata in figura la espressione nel caso di incidenza normale, ovvero per
θi
=0) ci dice quale frazione della potenza incidente viene riflessa.
?i
?r
legge di Snell:
?i=?r
n1 sen ?i =n2 sen ?t
mezzo 1
n1
Coefficiente di riflessione
R (?i =0)??n? ?n? ??/ ?n??n???
mezzo 2
n2
?t
Fig. 1 La discontinuità nell’indice di rifrazione fra due mezzi separati da una
superficie liscia provoca riflessione e rifrazione.
Scattering da superficie e da particelle
Se la superficie di separazione fra i due mezzi con diverso indice di rifrazione è estesa (molto
grande rispetto alla lunghezze d’onda) ma rugosa si ha il fenomeno dello scattering
(scattering=sparpagliamento; spesso si traduce, impropriamente, col termine diffusione)
20/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
ovvero il fascio di radiazione luminosa incidente viene sparpagliato in tutte le direzioni.
Analogo fenomeno si osserva se la radiazione investe una particella di dimensioni
paragonabili alla lunghezza d’onda della radiazione incidente. Il modo in cui la radiazione
viene sparpagliata dipende essenzialmente dall’indice di rifrazione dei due mezzi (o meglio
dal loro rapporto n1 n2 ), dalla lunghezza d’onda della radiazione e dalle dimensione
caratteristica della rugosità o della particella (o meglio dal rapporto fra la dimensione
caratteristica e la lunghezza d’onda).
Se lo ‘sparpagliamento’ avviene per effetto della rugosità superficiale (vetro smerigliato,
superficie graffiata, superficie increspata di un liquido, e comunque la quasi totalità delle
superfici degli oggetti che ci circondano) si parla di scattering da superficie.
Se lo ‘sparpagliamento’ avviene per effetto delle particelle di diverso indice di rifrazione
sospese nel mezzo in cui la luce si propaga (micro goccioline di acqua che costituiscono
nebbie e nubi; polvere sospesa nell’aria; membrane, nuclei e mitocondri nelle cellule di
tessuto biologico; particolato sospeso in acqua (es. micro particelle di grasso come nel caso
del latte)) si parla di scattering da particelle.
Scattering da superficie
Scattering da una particella
rad
iaz
ne
ion
s
o
i
c
z
a
a
t
i
t
era e
rad tterata
ta
sca
mezzo 1
n1
radiazione
incidente
rad
ia
sca zione
tter
ata
mezzo 1
n1
mezzo 2
n2
mezzo 2
n2
e
ion
iaz ata
rad atter
sc
ne
zio te
a
i
n
rad cide
in
e
ion
iaz rata
rad atte
sc
Fig. 2 Il fenomeno dello scattering è dovuto alla discontinuità nell’indice di
rifrazione quando la superficie di separazione è rugosa (scattering da
superficie) o quando le dimensioni della particella sono paragonabili alla
lunghezza d’onda della radiazione incidente (scattering da particelle)
Assorbimento
La luce propagandosi nei mezzi naturali può essere assorbita. L’assorbimento dipende dal
tipo di molecole di cui il mezzo è costituito: ogni molecola interagendo con la radiazione
luminosa ne può assorbire una frazione che solitamente riemette a lunghezze d’onda molto
maggiori (sotto forma di calore). Lo spettro di assorbimento (ovvero la dipendenza
dell’assorbimento dalla lunghezza d’onda della radiazione incidente) è caratteristico di ogni
molecola.
21/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Lo scattering dovuto alle particelle sospese nel mezzo attraversato dalla radiazione luminosa,
e l’assorbimento delle molecole che costituiscono il mezzo determinano la torbidità del
mezzo
Propagazione di un fascio di luce collimata in presenza di assorbimento e di scattering
da particelle sospese nel volume del mezzo attraversato
Un fascio di radiazione che si propaga in un mezzo torbido subisce in generale sia gli effetti
di assorbimento che di scattering: parte della radiazione viene assorbita, parte scatterata e una
parte viene trasmessa. Mentre la parte di radiazione assorbita ‘scompare’ alla nostra vista, la
parte scatterata continua a propagarsi nel mezzo subendo eventualmente altri eventi di
scattering finché non viene a sua volta assorbita o eventualmente fuoriesce dal mezzo (questa
frazione è quella responsabile della luminosità diffusa che osserviamo per esempio
illuminando con un fascio di luce un mezzo lattiginoso).
Mezzo torbido
Pe
P(z)
z
P(z)+dP
P0
dz
d
Fig. 3 Attenuazione del fascio di radiazione luminosa per effetto dello
scattering e dell’assorbimento: della radiazione P(z) che incide sull’elemento di
volume di spessore dz a profondità z una parte viene deviata per effetto dello
scattering ed una viene assorbita (raggi interrotti)
Come conseguenza un fascio di radiazione di potenza Pe attraversando un mezzo
torbido viene attenuato. Come esemplificato in Fig. 3 ogni elemento di volume, per effetto
dello scattering dovuto al particolato sospeso nel mezzo e dell’assorbimento, sottrae una
frazione della radiazione che lo investe che risulta essere proporzionale allo spessore del
volume stesso. Con riferimento alla figura, se indichiamo con P(z) la potenza che incide sul
volumetto di spessore e con P(z)+dP quella che riemerge dal volumetto senza aver subito
scattering o assorbimento possiamo esprimere questo fatto scrivendo:
dP
= −µ ext dz = −(µ s + µ a )dz
P( z )
22/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
(1)
dove µext è un coefficiente caratteristico del mezzo torbido chiamato coefficiente di
estinzione. Le sue dimensioni sono l’inverso di una lunghezza (lo misureremo in mm-1). Il
coefficiente di estinzione lo si può scrivere come somma del coefficiente di scattering µs, che
descrive la frazione della radiazione estratta per scattering, e del coefficiente di assorbimento
µa, che descrive la frazione della radiazione estratta per assorbimento.
La soluzione dell’equazione (1) è la seguente:
P( z ) = P e e −µext z ,
(2)
come si può verificare derivando la (2) ( dP = − P e µ ext e −µext z dz = −µ ext P( z )dz ) ed
osservando che per z = 0 la soluzione soddisfa la condizione P( z = 0) = P e . Se indichiamo
con PO la potenza del fascio che riemerge dallo strato di spessore d senza essere stata
assorbita o scatterata otteniamo dalla (2):
P0 = P( z = d ) = P e e −µext d
(3)
L’equazione (3), che descrive la attenuazione di un fascio di radiazione nella
propagazione attraverso uno strato di mezzo torbido, è comunemente indicata come legge di
Lambert-Beer. Questa legge è alla base delle misure spettrofotometriche.
23/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1
Osservazione
Sono le proprietà di scattering e di assorbimento delle superfici e dei volumi dei mezzi che ci
circondano che ci fanno apparire il mondo così come lo vediamo. La sorgente luminosa, ad
esempio il sole o una lampada, illuminano la scena osservata. Ogni elemento delle superfici
degli oggetti investiti dalla luce, ed ogni microparticella sospesa nel volume attraversato
‘scattera’ in tutte le direzioni una frazione della luce incidente ed agisce quindi come una
sorgente secondaria di luce. Una frazione della luce riemessa da queste sorgenti secondarie
raggiunge il nostro occhio che provvede a formare l’immagine della scena osservata.
Solitamente il colore degli oggetti che osserviamo è determinato dalle proprietà di
assorbimento (es: un oggetto illuminato con luce bianca appare rosso se assorbe la luce di
colore diverso dal rosso). Una eccezione importante si ha per l’atmosfera limpida: in questo
caso l’azzurro del cielo è determinato dalle proprietà di scattering dell’atmosfera che, essendo
dovute essenzialmente alle molecole dei gas atmosferici (e quindi di dimensioni molto
piccole rispetto alla lunghezza d’onda), dipendono fortemente dalla lunghezza d’onda.
Le proprietà di scattering e quelle di assorbimento sono responsabili della torbidità del
mezzo. Le scene più belle che possiamo osservare sono tali grazie allo scattering e
all’assorbimento. Proviamo ad immaginare il mondo come lo vedremmo se non ci fosse
scattering!
24/24 - Modulo Fisica -Lab Bio Sper I/gp/rev.11/1