Quantizzazione delle energie
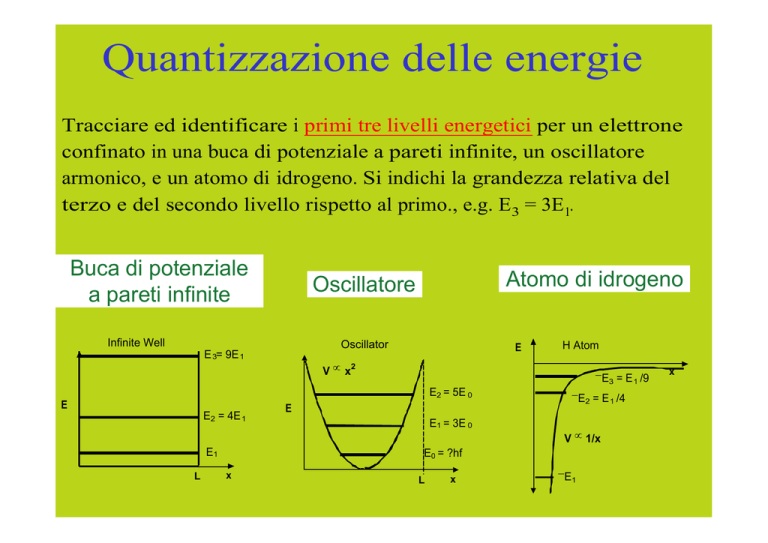
Tracciare ed identificare i primi tre livelli energetici per un elettrone
confinato in una buca di potenziale a pareti infinite, un oscillatore
armonico, e un atomo di idrogeno. Si indichi la grandezza relativa del
terzo e del secondo livello rispetto al primo., e.g. E3 = 3E1.
Buca di potenziale
a pareti infinite
Atomo di idrogeno
Oscillatore
Infinite Well
Oscillator
E 3= 9E 1
E
V ∝ x2
−E3 = E 1 /9
E2 = 5E 0
E
E2 = 4E 1
E1
L
H Atom
E
E1 = 3E 0
−E2 = E 1 /4
V ∝ 1/x
E0 = ?hf
x
L
x
−E1
x
1. L‘atomo di idrogeno
1.1. Comportamento in campo centrale
Equazione di Schroedinger indipendente dal tempo
∆
(x,y,z) → ( R,θ,φ )
Coordinate sferiche:
x=r sinθ cosφ
y= r sinθ sinφ
z=r cosθ
Equazione di Schroedinger agli stati stazionari per un potenziale centrale
Separazione delle variabili: Ψ(r,θ ,φ )= R(r) T(θ) P(φ)
Dipende solo da r e θ
Dipende solo da φ
Entrambi i membri devono essere posti uguali a una costante C1
Soluzione:
Affinché la funzione sia univoca, deve valere: P(φ)=P(φ + nπ)
Dividiamo per
Numero intero (m)
m=0, +1, +2, ...
Equazione di Schroedinger agli stati stazionari per un potenziale centrale
Separazione delle variabili: Ψ(r,θ ,φ )= R(r) T(θ) P(φ)
C 1 = ml 2
Dipende solo da r,θ
Dipende solo
da φ
Dipende solo da θ
Dipende solo da r
Entrambi i membri devono essere uguali a una costante C2
sostituzione ξ=cosθ !
m 2
1 d
2 dT
1− ξ
+ C2 −
T = 0
2
2
r dξ
dξ
1− ξ
(
)
Equazione di
Legendre
Soluzione generale: funzioni di Legendre Plm
T=Plm (cos(θ))
C2 = l(l+1), l =m, m+1, …
T(θ) P(φ) = Plm (cos(θ)) e imφ = Y lmm(θ,φ)
εZ
Armoniche sferiche
Osservazione: Momento angolare in meccanica quantistica
Grandezza fisica
→
vettore posizione
r
→
quantità di moto
p
Operatore
Osservazione: Momento angolare in meccanica quantistica
Grandezza fisica
→
vettore posizione
r
→
quantitàdi moto
p
Operatore
l = 0,1,2,3 ....
-l<ml<l
Numero quantico azimutale
Numero quantico magnetico
Relazioni di indeterminazione per l’impulso:
1
∆Lx ∆Ly ≥ ψ [Lx ,Ly ] ψ
2
z
m~
2
L e Lz
sono misurabili simultaneamente
x,y componenti indeterminate Esempio: l=2
m=-2,-1,0,1,2
1. La lunghezza del vettore é quantizzata!
2. Non può avere una direzione qualsiasi
nello spazio: La direzione é quantizzata!
Asse di quantizzazione
sviluppare
negativo
Per r→∞ si trascurano 1/r e 1/r2
Soluzione completa (Polinomi di Laguerre):
Dipende da n e l
Limiti per l
l<0,1,2,... n
Come nel modello di Bohr!
NON
dipende da l
Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = R nl(r) Ylm(θ φ)
Numero quantico:
Simbolo
principale
n = 1,2,...
azimutale
l = 0,1,2,3,4... (n-1)
s,p,d,f
magnetico
(proiezione del
Momento angolare)
n2 possibilità
-l < m < l
Stato fondamentale n=1 l=0 m=0
n=2 l=0 m=0
l=1 m=-1
m=0
m=1
Non c’é orbita di Bohr!
Momento angolare NULLO.
“degeneri” (medesima energia)
Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = R nl(r) Ylm(θ φ)
|Rnl(r)|2 dV
probabilità di trovare un
elettrone in un
elemento di volume dV a
distanza r dal nucleo
r2|Rnl(r)|2 dr
probabilità di trovare un
elettrone in un guscio sferico
a distanza r dal nucleo
“massimo” sul nucleo!
Massimo in corrispondenza
Del raggio di Bohr
Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = R nl(r) Ylm(θ φ)
|Rnl(r)|2 dV
Probabilità di trovare un
elettrone in un elemento di
volume dV a distanza r
dal nucleo
r2|Rnl(r)|2 dr
Probabilità di trovare un
elettrone in un guscio sferico
di spessore dr
a distanza r dal nucleo
punto nodale!
Regione
Proibita
classicamente
Tunneling
Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = R nl(r) Ylm(θ φ)
Y00 = C1
Y10= C2 cosθ
Y11= C3 sinθ eiφ
Y20=C4(2cos2θ –sin2θ)
Y21=C5(cosθ –sinθ eiφ
Y22=C6 sin2 θ e2iφ
Rappresentazione polare:
Asse Z
(asse di quantizzazione)
Ψnlm(r,θ,φ)= Rnl(r) T(θ)lm Pm(φ) = R nl(r) Ylm(θ φ) Asse di quantizzazione
Y00 = C1
Y10= C2 cosθ
Y11= C3 sinθ eiφ
Y20=C4(2cos2θ –sin2θ)
Y21=C5(cosθ –sinθ eiφ
Y22=C6 sin2 θ e2iφ
Rappresentazione polare
Confronto Modello di Bohr - Meccanica Quantistica
Meccanica quantistica
Densità di probabilità
Modello di Bohr
Orbite planetarie
rn
Raggio
dell‘ „orbita“
Densità di prob.
Momento angolare
rn=a0/Z n2
Vicino a r=0 può essere max.
Nulla per r=0
L=nh
Funzioni d’onda
Componente sferica Yl,m
orbitale s
Funzione d’onda completa ψn,l,m
n=1
l=0
l=0
m = ±1
orbitali p
n=2
l=1
l = 0,1
orbitali d
l=2
l = 1 m = ±1
orbitali f
l=3
n=3
l = 0,1,2
da: http://www.uniovi.es/~quimica.fisica/qcg/harmonics/charmonics.html
m = –3
m = –2
l=0
m = –1
m=0
m=1
sinθ sinφ
cosθ
sinθ cosφ
sinθcosθ
sinφ
3cos2θ–1
sinθcosθ
cosφ
m=2
m=3
orbitale s
l=1
orbitali p
2 lobi
l = 2 orbitali d
4 lobi
sin2θ sin2φ
sin2θ cos2φ
l=3
6 lobi
sin3θ
sin3φ
sin2θ cosθ sinθ(5cos2
sin2φ
θ−1) sinφ
5cos3θ– sinθ(5cos2θ sin2θ cosθ
3cosθ
−1) cosφ
cos2φ
sin3θ
cos3φ
l = 0 orbitali s
100
l=1
orbitali p
da: http://pcgate.thch.uni-bonn.de/tc/people/
hanrath.michael/hanrath/HAtomGifs.html
l=2
200
211 210
300
311 310 311
322
321 320
321
322
400
411 410
422
421 420
421
422
431 430 431
432
433
l=3
211
orbitali d
411
orbitali f
433
432
Rimozione della degenerazione in l
Nell‘atomo di idrogeno E non dipende da l
Numero quantico:
principale
Momento angolare
magnetico
(proiezione del
momento angolare)
Simbolo
n = 1,2,...
l = 0,1,2,3,4... (n-1) Nell‘atomo di H influenzano
la funzione d‘onda
s,p,d,f
ma NON l‘energia
-l < m < l
Uguali autovalori!
Vale solo per il potenziale Coulombiano
Rimozione della degenerazione in l
Diagramma di Grotrian
per l’atomo di Litio
Litio
n=1
Z=3
L‘elettrone esterno
„vede“ uno Z=1?
En =13,6/n2 per n>2 ??
La degenerazione in l é rimossa!
L‘elettrone 2s é più legato di quello 2p
Rimozione della degenerazione in l
probabilità per
l‘elettrone 2s all‘interno
del guscio 1s
Potenziale
schermato
La degenerazione in l é rimossa!
L‘elettrone 2s é più legato di quello 2p
Z=3
Z=1
Approssimazione:
Si trascurano le correlazioni elettroniche
Consideriamo il caso dell‘atomo di sodio
Diagramma di Grotrian
per l’atomo di sodio
Emissione nel giallo
589 nm
Na: 2 elettroni per n=1
6 elettroni per n=2
1 elettroni per n=3












