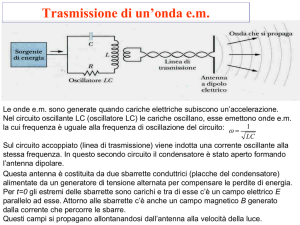
LA LEZIONE
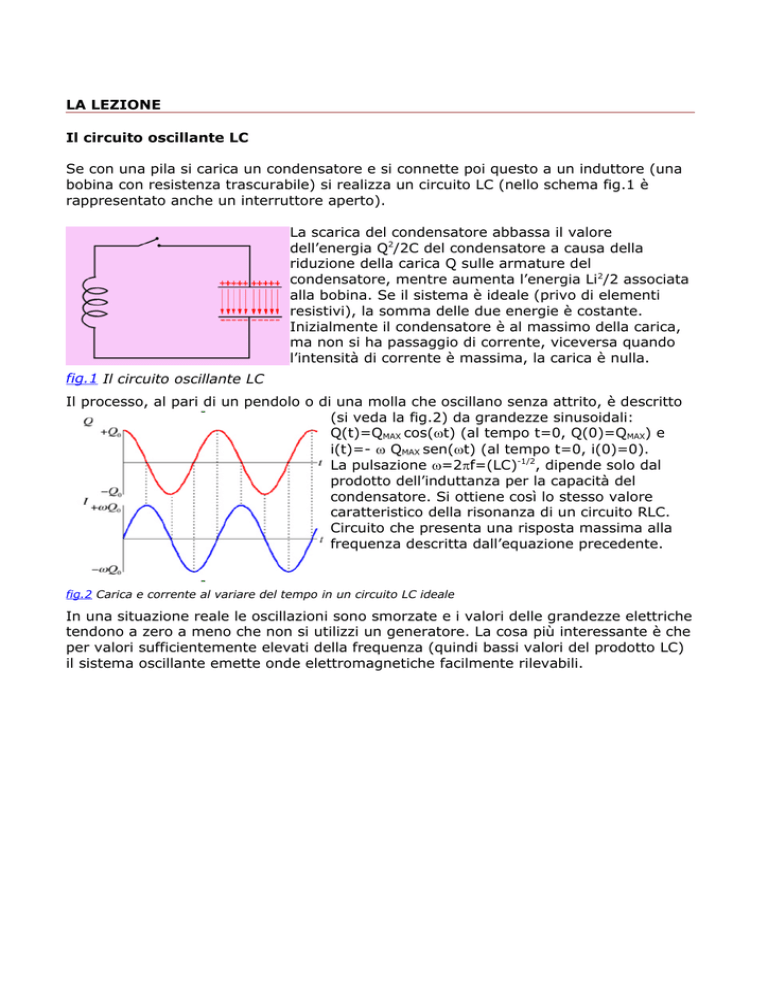
Il circuito oscillante LC
Se con una pila si carica un condensatore e si connette poi questo a un induttore (una
bobina con resistenza trascurabile) si realizza un circuito LC (nello schema fig.1 è
rappresentato anche un interruttore aperto).
La scarica del condensatore abbassa il valore
dell’energia Q2/2C del condensatore a causa della
riduzione della carica Q sulle armature del
condensatore, mentre aumenta l’energia Li2/2 associata
alla bobina. Se il sistema è ideale (privo di elementi
resistivi), la somma delle due energie è costante.
Inizialmente il condensatore è al massimo della carica,
ma non si ha passaggio di corrente, viceversa quando
l’intensità di corrente è massima, la carica è nulla.
fig.1 Il circuito oscillante LC
Il processo, al pari di un pendolo o di una molla che oscillano senza attrito, è descritto
(si veda la fig.2) da grandezze sinusoidali:
Q(t)=QMAX cos(t) (al tempo t=0, Q(0)=QMAX) e
i(t)=- QMAX sen(t) (al tempo t=0, i(0)=0).
La pulsazione =2f=(LC)-1/2, dipende solo dal
prodotto dell’induttanza per la capacità del
condensatore. Si ottiene così lo stesso valore
caratteristico della risonanza di un circuito RLC.
Circuito che presenta una risposta massima alla
frequenza descritta dall’equazione precedente.
fig.2 Carica e corrente al variare del tempo in un circuito LC ideale
In una situazione reale le oscillazioni sono smorzate e i valori delle grandezze elettriche
tendono a zero a meno che non si utilizzi un generatore. La cosa più interessante è che
per valori sufficientemente elevati della frequenza (quindi bassi valori del prodotto LC)
il sistema oscillante emette onde elettromagnetiche facilmente rilevabili.
I primi esperimenti sulle onde elettromagnetiche
Heinrich Hertz nel 1887 fu il primo a misurare
indipendentemente la lunghezza d’onda delle
onde radio emesse da un circuito oscillante di
frequenza nota, arrivando a un risultato
prossimo alla velocità della luce. Alla base del
generatore di onde radio di Hertz vi era un
rocchetto di Ruhmkorff (illustrato nella fig.3)
capace di generare, per induzione, scariche
elettriche tra i poli.
Oltre al rocchetto e alla pila, il circuito
conteneva un emettitore (variabile nello
sviluppo delle esperienze di Hertz) costituito da
condensatori, bacchette e sferette tra cui
scoccavano le scintille.
fig.3 Rappresentazione schematica di un rocchetto di Ruhmkorff: A, nucleo; b, avvolgimento primario; c,
secondario; d, poli; e, morsetti di connessione al circuito di alimentazione; f, batteria; g, interruttore (che
viene aperto e chiuso in rapida successione, in modo che la corrente diventi pulsante)
Il ricevitore, a sua volta era invece un semplice anello aperto alle cui estremità erano
fissate due sferette molto vicine (si veda lo schema di fig.4 e la riproduzione di uno
degli apparati di Hertz di fig.5).
fig.4 Circuiti utilizzati nell’esperimento di Hertz del 1887; fig.5 Riproduzione dell’apparato sperimentale di
Hertz
La strumentazione era completata da alcuni micrometri necessari per valutare la
lunghezza delle scintille. Nelle figure 6A e 6B è evidenziato il funzionamento
dell’apparato. Nel disegno le onde elettromagnetiche non sono rappresentate in scala
rispetto alle dimensioni dell’apparato di misura.
fig.6 Schema dell’emissione (A) e della
ricezione (B) dell’onda
elettromagnetica nell’esperimento di
Hertz del 1887
Variando le dimensioni della spira del ricevitore si ottenevano scintille di diversa
lunghezza. Riportando su un grafico la lunghezza delle scintille in funzione della
circonferenza dell’anello, Hertz ottenne figure di risonanza (fig.7).
La misura diretta della lunghezza d’onda fu realizzata invece ipotizzando la formazione
di onde radio stazionarie in un’aula avente una parete ricoperta con una lastra di zinco.
Muovendo il ricevitore all’interno della stanza e cercando i nodi dell’onda il fisico trovò
per la metà della lunghezza d’onda un valore prossimo a 4,80 metri, come è
rappresentato nel disegno originale tratto da uno dei suoi lavori (fig.8).
fig.7 Grafici di risonanza ottenuti da Hertz, variando le dimensioni della spira e misurando la lunghezza delle
scintille nel ricevitore; fig.8 Le onde stazionarie e la misura della lunghezza d’onda caratteristica negli articoli
originali di Hertz
Il perfezionamento dello studio delle onde elettromagnetiche e della loro riflessione
proseguì nel 1888 con apparecchiature capaci di produrre frequenze più elevate e
riflettori parabolici per le onde radio simili a specchi concavi per la luce. Il sistema a
scintille di Hertz prima dell’avvento dei tubi elettronici a vuoto (le valvole) divenne la
base per la generazione delle onde radio utilizzate in radiotelegrafia. Il ricevitore era
invece costituito da un semplice circuito in cui un elemento (coherer) era sensibile al
passaggio dell’onda.
Le antenne e la radiazione di dipolo elettrico
Nel campo delle telecomunicazioni le onde radio hanno frequenze molto variabili. Ad
una frequenza di 1MHz corrisponde una lunghezza d’onda di 300 metri, mentre per un
segnale delle onde corte con f=1GHz, =0,3 m. Per questioni pratiche l’antenna
ricevente non potrà allora avere sempre dimensioni confrontabili con la lunghezza
caratteristica dell’onda. Nel caso delle onde corte è possibile realizzare un sistema
risonante per molti versi simile (fatte le opportune analogie tra onde radio e sonore)
alla cassetta di risonanza di un diapason che emette un suono puro. Un circuito
elettrico oscillante, come abbiamo ricordato più volte, è definito da una corrente o una
tensione sinusoidale di frequenza f. Se un generatore in alternata alimenta le estremità
di una coppia di sottili fili metallici, l’effetto complessivo (nel caso in cui i cavi di
collegamento non diano un segnale riflesso) è quello di una carica che accelera
verticalmente lungo il percorso AB oscillando periodicamente (fig.9).
La carica accelerata è oggi la più comune sorgente di onde elettromagnetiche di
frequenza f che irradiano dall’antenna. La lunghezza complessiva dell’antenna l (fig.10)
è molto vicina al valore della metà della lunghezza d’onda (a livello pratico si pone l =
0,475 ). Il profilo dell’onda stazionaria all’interno del dipolo assume ad esempio a un
certo istante un massimo al centro (dove l’impedenza è dell’ordine di 50-75 ohm) e
valori prossimi a zero alle estremità (impedenze comprese tra 5 e 6 migliaia di ohm),
simile alle oscillazioni di una corda fatta oscillare tra gli estremi A e B.
fig.9 Nello schema un generatore oscillante ad alta frequenza produce all’interno del filo una corrente lungo il
filo che si può immaginare solo oscillante lungo la direzione verticale individuata dai punti A e B; fig.10
Nell’esempio in figura un’onda di frequenza 150 MHz che viaggia alla velocità della luce ha una lunghezza
d’onda di 2 m, quindi la metà della lunghezza d’onda è 1 m. La lunghezza complessiva del dipolo è invece di
98 cm
L’antenna irradia dal centro del dipolo. Un ricevitore avrà la stessa forma dell’antenna
di trasmissione e le correnti amplificate potranno essere rilevate da un circuito
terminante con un segnale audio o uno strumento di misura. In un’esperienza di
ricezione come quella descritta dai vecchi filmati PSSC (si veda il video 7), la
disposizione delle antenne trasmittenti e riceventi non potrà essere casuale. Solo
mettendo le due antenne parallele si otterrà una risonanza. Il campo elettrico a causa
della polarizzazione dell’onda segue il verso delle cariche accelerate e quindi l’onda è
polarizzata a seconda della disposizione del dipolo (fig.11).
Per concludere, si possono dimezzare le dimensioni dell’antenna risonante collegando
una delle estremità dei fili a terra con il metodo seguito per la prima volta da Marconi
(fig.12).
fig.11 Un esempio di antenna polarizzata verticalmente è quello relativo alle trasmissioni radio in onde
medie. Onde polarizzate orizzontalmente (rispetto alla superficie terrestre) sono quelle utilizzate nelle
trasmissioni televisive; fig.12 Monopolo o antenna di Marconi. Anche in questo caso la lunghezza
dell’antenna non è esattamente uguale a un quarto della lunghezza d’onda