LAVORO DI INFORMATICA
A.S. 2011/2012
CLASSE IV°A
LA STORIA DELLA GEOMETRIA
Secondo Erodoto, uno storico greco antico, raccontò che sotto il regno del
faraone Ramsete II (1.300 a.C.), la superficie dell’Egitto era diviso in tanti
appezzamenti di terreno, cioè la terra da coltivare era divisa in tanti recinti.
Il faraone, per poter permettere ai contadini di coltivare la terra , mise una
tassa annuale ( tributo), cioè un pagamento in monete o in natura.
Ma con l’inondazione del Nilo , considerato il fiume più lungo del mondo,
alcune parti di terra furono coperte e quindi si dovette procedere ad una
nuova misurazione della superficie, così nacque la geometria.
Infatti la parola geometria significa “ misurazione della terra “.
La geometria dall’Egitto si diffuse poi in Grecia dove si ebbero i piu’
grandi sviluppi, ricordiamo alcuni matematici.
- Pitagora ( Samo, 570 a.C. ): studiò il triangolo;
- Euclide ( Gela, 323 a.C. ) : considerato il fondatore della geometria;
- Archimede ( Siracusa, 287 a.C.) : studiò il cerchio.
EGITTO
PITAGORA
ARCHIMEDE
GEOMETRIA EUCLIDEA
La geometria che studieremo prende il nome del suo studioso,
geometria euclidea.
Gli elementi fondamentali della geometria euclidea sono:
- il punto;
- la retta;
- il piano ( superficie).
EUCLIDE
REGIONE ESTERNA, REGIONE
INTERNA E CONFINE
Una linea chiusa (definita confine ) determina una
REGIONE INTERNA e una REGIONE ESTERNA.
Regione interna: spazio che c’è dentro;
Regione esterna: spazio che c’è fuori;
Confine: linea chiusa che separa lo spazio interno da quello
esterno.
REGIONE
INTERNA
REGIONE ESTERNA
CONFINE
IL PUNTO E LO SPAZIO
Il punto è la figura geometrica più semplice.
Le sue caratteristiche sono:
- indicato con la lettera maiuscola dell’alfabeto;
- non ha una dimensione;
- non ha una posizione;
- non ha una lunghezza;
- non ha una altezza.
LO SPAZIO
Lo spazio è un insieme di punti distribuiti su un piano.
Con la tecnica del “ puntinismo” coloriamo gli spazi (triangoli ) dentro il
quadrato utilizzando colori diversi.
LA LINEA
La linea è una serie infinita di punti consecutivi, cioè uno dietro l’altro.
LINEA CHIUSA E LINEA APERTA
Linea chiusa: quando il punto di partenza ( A ) coincide con il punto di
arrivo.
La linea chiusa si distingue in :
- semplice: senza intrecci;
- intrecciata: con intrecci (nodo).
LINEA CHIUSA
SEMPLICE
LINEA CHIUSA
INTRECCIATA
Linea aperta: quando il punto di partenza ( A) non coincide con il punto di
arrivo ( B).
La linea aperta si distingue in :
- semplice: senza intrecci;
- intrecciata: con intrecci ( nodo).
LINEA APERTA
SEMPLICE
LINEA APERTA
INTRECCIATA
ALTRI TIPI DI LINEE
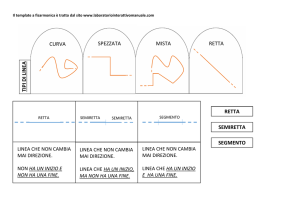
La linea si distingue in quattro tipi: retta, curva, spezzata e mista.
1) RETTA: orizzontale, verticale e obliqua.
LINEA
ORIZZONTALE
LINEA
VERTICALE
LINEA
OBLIQUA
2) CURVA: chiusa e aperta
LINEA CURVA
CHIUSA APERTA
LINEA CURVA
3) SPEZZATA: chiusa e aperta
LINEA SPEZZATA
CHIUSA
LINEA SPEZZATA
APERTA
4) MISTA: chiusa e aperta
LINEA MISTA
CHIUSA
LINEA MISTA
APERTA
DISEGNO CON LE LINEE
ALTRI TIPI DI LINEE ( RETTE )
RETTA
La retta è una linea infinita: non ha un inizio e né una fine.
Retta
Se fissiamo un punto nella mia retta, creiamo due semirette, una semiretta
a sinistra e una semiretta a destra.
SEMIRETTA
La semiretta è una linea che ha un inizio, ma non ha una fine.
Semiretta sinistra
Semiretta destra
Se fissiamo due punti nella mia retta, creiamo un segmento.
SEGMENTO
Il segmento ha un inizio e una fine.
Segmento
RETTE PARALLELE, INCIDENTI E
PERPENDICOLARI
Le rette possono essere di tre tipi: parallele, incidenti e perpendicolari.
1) RETTE PARALLELE: non si incontrano mai e mantengono tra loro
sempre la stessa distanza;
2) RETTE INCIDENTI: rette che si incontrano in un punto comune (A);
3) RETTE PERPENDICOLARI: rette incidenti che si incontrano in un
punto comune (O), formando 4 angoli retti ( 90°).
SEGMENTI CONSECUTIVI E ADIACENTI
I segmenti possono essere di due tipi: consecutivi e adiacenti.
1) SEGMENTI CONSECUTIVI: quando un estremo in comune ( B);
2) SEGMENTI ADIACENTI: quando hanno un estremo in comune (B) e
appartiene alla stessa retta.
GLI ANGOLI
ANGOLO: è lo spazio compreso tra due semirette (lati) che
iniziano nello stesso punto (vertice).
lato
ampiezza
Vertice
lato
L’angolo può essere:
- concavo: angolo interno alle due semirette;
- convesso: angolo esterno sul prolungamento delle due
semirette.
Concavo
Convesso
TIPI DI ANGOLI
Gli angoli vengono classificati in base alla loro ampiezza.
ANGOLO RETTO: 90 °
ANGOLO PIATTO:180°
ANGOLO GIRO: 360°
ANGOLO ACUTO:
minore (< 90° )
ANGOLO OTTUSO:
maggiore ( > 90°)
POLIGONO
La parola poligono deriva dal greco antico e significa “ molti angoli”.
Il poligono è una figura geometrica piana delimitata da una linea chiusa
spezzata, detta contorno del poligono.
Il contorno del poligono si chiama PERIMETRO, mentre la sua
superficie si chiama AREA.
Esercizio: Colora il perimetro di rosso e l’area di giallo.
CLASSIFICAZIONE DEI POLIGONI
I poligono vengono classificati in base al numero dei:
-lati
-angoli
-vertici
●TRIANGOLI: 3 lati, 3 angoli e 3 vertici;
Triangolo
●QUADRILATERI: 4 lati, 4 angoli e 4 vertici;
Quadrato
Trapezio
Parallelogramma
●POLIGONI CON PIU’ di 4 lati, 4 angoli e 4vertici;
Pentagono
Esagono
CARATTERISTICHE DEI POLIGONI
Il poligono è formato da una serie di elementi: lati, vertici, angoli interni,
diagonali.
Lati: segmenti della linea spezzata;
Vertici: punti in cui si incontrano i lati;
Angoli interni: angoli che formano i lati;
Diagonali: segmenti che uniscono due vertici con consecutivi.
Legenda:
- Vertici: A, B, C, D;
- Lati: AB, BC, CD, DA;
- Angoli: A,B,C,D;
- Diagonale: AC, BD.
BASE E ALTEZZA
Le figure geometriche piane, non avendo uno spessore, sono costituite solo
da due dimensioni :
-Base (B): lato su cui cade l’altezza;
-Altezza ( h): segmento che parte da un vertice e cade
perpendicolarmente sul lato opposto ( base) formando angoli retti (90°).
Esercizio: Ripassa di rosso l’altezza e di blu la base dei seguenti poligoni.
Triangolo
Quadrato
Rettangolo
Parallelogrammo
Trapezio
IL TRIANGOLO
Tutti i triangoli hanno queste caratteristiche comuni :
● 3 lati;
● 3 angoli;
● 3 vertici;
I triangoli si possono classificare in base ai :
- LATI
Triangolo
Equilatero
( tutti i lati uguali)
Triangolo
Isoscele
( due lati uguali)
Triangolo
Scaleno
( tutti i lati diversi)
-ANGOLI
Triangolo
Rettangolo
( ha un angolo retto
di 90° e due acuti)
Triangolo
Acutangolo
( ha tutti gli angoli
acuti < di 90° )
Triangolo
Ottusangolo
( ha un angolo ottuso
> di 90° e due acuti )
Ricorda: In tutti i triangoli la somma degli angoli interni è di 180°,
cioè un angolo piatto.
FORMULE
● PERIMETRO
-Triangolo Equilatero:
P = (L ) x 3
1
-Triangolo Isoscele:
P=(L x2 )+L
1
3
-Triangolo scaleno:
P=L +L + L
1
2
3
● AREA
A=(bxh):2
b=(Ax2):h
h = ( A x 2) : b
● LATO
L1 = P- ( L2 + L3 )
L2 = P- ( L1 + L3)
L3 = P - ( L1 + L2)
IL QUADRATO
Il quadrato è un quadrilatero che ha:
● 4 lati tutti uguali ( Equilatero);
● 4 angoli tutti uguali 90° ( Equiangolo);
Ricorda: Nel quadrato la somma degli angoli interni è di 360°, cioè un
angolo giro.
FORMULE
● PERIMETRO
P=LX4
● AREA
A=LXL
● LATO
L = A: L
IL RETTANGOLO
Il rettangolo è un quadrilatero che ha:
● 2 lati corti uguali ( altezza);
● 2 lati lunghi uguali ( base);
● 4 angoli retti ( 90°).
Ricorda: Nel rettangolo la somma degli angoli interni è di 360°, cioè un
angolo giro.
Legenda:
AC e BD: altezze
AB e CD: basi
FORMULE
● PERIMETRO
P= ( b + h )X
2
● AREA
A=bxh
● BASE
b = ( P : 2) – h
b=A:h
● ALTEZZA
h= ( P : 2) - b
h= A : b