NOTE INTEGRATIVE SULL’ECCESSO DI PRESSIONE
Con eccesso di pressione si indica una situazione di inefficienza all’interno del sistema tributario
determinata dal fatto che l’introduzione di un’imposta influisce sull’allocazione delle risorse,
pertanto influisce sulle scelte dei consumatori attraverso una variazione dei prezzi relativi.
Da cosa dipende l’entità dell’eccesso di pressione?
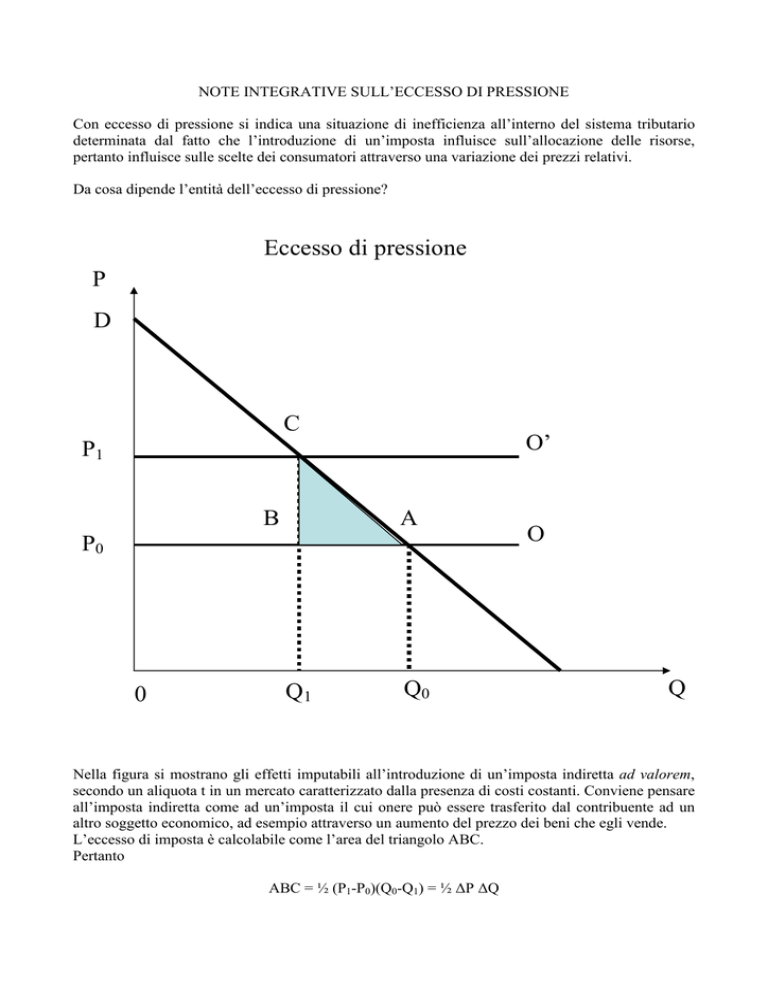
Eccesso di pressione
P
D
C
O’
P1
B
A
P0
0
Q1
Q0
O
Q
Nella figura si mostrano gli effetti imputabili all’introduzione di un’imposta indiretta ad valorem,
secondo un aliquota t in un mercato caratterizzato dalla presenza di costi costanti. Conviene pensare
all’imposta indiretta come ad un’imposta il cui onere può essere trasferito dal contribuente ad un
altro soggetto economico, ad esempio attraverso un aumento del prezzo dei beni che egli vende.
L’eccesso di imposta è calcolabile come l’area del triangolo ABC.
Pertanto
ABC = ½ (P1-P0)(Q0-Q1) = ½ ∆P ∆Q
Per poter svolgere delle considerazioni di carattere normativo, in grado quindi di dare indicazioni di
politica fiscale, è necessario riscrivere la formula precedente mettendo in luce il ruolo che
l’elasticità della domanda e l’aliquota marginale d’imposta assumono quando si ragiona in termini
di eccesso di imposta.
L’elasticità della domanda rispetto al presso è data dal rapporto tra la variazione proporzionale della
quantità Q e la corrispondente variazione proporzionale del prezzo P. Fornisce un’indicazione della
sensibilità di Q alle variazioni di P. Tale indicazione - a differenza di quella fornita dalla derivata –
è indipendente dall’unità di misura di Q e di P.
E = EQ,P = (∆Q/∆P) P/Q
L’aliquota d’imposta t è ricavabile dalla stessa definizione di imposta indiretta ad valorem.
Infatti riferendosi al grafico precedente vale che
P1 = P0(1+t), cioè
P1 = P0 + tP0, da cui
t = (P1- P0)/P0 = ∆P/P
Pertanto possiamo scrivere l’area del triangolo ABC come segue:
ABC = ½ ∆P ∆Q =
= ½ (∆Q/∆P) (P/Q) (Q/P) ∆P ∆P
Nella formula precedente in rosso appare la formula dell’elasticità E = (∆Q/∆P) P/Q;
appaiono sottolineate le variabili presenti nell’equazione di partenza, cioè ½ ∆P ∆Q ;
in verde appaiono invece quelle variabili necessarie a garantire l’identità con la prima definizione.
Infatti se si moltiplica Q/P con P/Q si ottiene 1. Anche se si moltiplica ∆P con 1/∆P si ottiene 1.
Svolte queste due moltiplicazioni si torna esattamente all’equazione di partenza, pertanto si tratta di
trasformazioni legittime.
Data la definizione di elasticità possiamo scrivere
ABC = ½ E Q/P ∆P ∆P
Per introdurre anche l’aliquota t occorre trasformare ulteriormente la formula, evidenziando la
relazione (∆P/P):
ABC = ½ E Q/P ∆P ∆P = ½ E Q (∆P/P) ∆P
= ½ E Q t ∆P
Abbiamo introdotto t, ma conviene però trasformare ulteriormente la nostra formula moltiplicando e
dividendo per ∆P/P. Questa trasformazione è ancora una volta legittima, perché equivale a
moltiplicare la formula per 1: infatti (∆P/P) (P/∆P) = 1 . Si ha allora :
ABC = ½ (E Q t ∆P) (∆P/P) (P/∆P)
Possiamo allora semplificare ∆P con (P/∆P) ottenendo P, infatti ∆P/∆P è uguale ad 1. Possiamo
anche riscrivere (∆P/P) come t. Si ha allora:
ABC = ½ (E Q t) t P
Si ottiene allora, una relazione che può mettere in luce le due proprietà fondamentali dell’eccesso di
imposta causato dall’introduzione di un’imposta indiretta ad valorem.
ABC = ½ E t2 QP
1. L’eccesso di pressione è funzione positive dell’elasticità della domanda.
In termini di politica fiscale ciò vuol dire che lo stato può perseguire risultati efficienti in
termini allocativi, tassando i beni ad elasticità minore (i beni di prima necessità).
2. L’eccesso di pressione aumenta più che proporzionalmente all’aumentare dell’aliquota
marginale d’imposta.
In termini di politica fiscale questo significa che per ridurre gli effetti distorsivi
dell’imposizione è necessario (a parità di gettito) distribuire il carico tributario su più beni. (uno
dei fondamenti del principio della flat tax).
Stefano Lucarelli