Un algoritmo di calcolo parallelo per attaccare i problemi

Un algoritmo di calcolo parallelo per attaccare i problemi RSA
Di Cristiano Armellini ([email protected])
Sia dato un tipico problema RSA ovvero dobbiamo trovare i fattori primi p, q nel numero n = pq molto
grande. Supponiamo senza perdere di generalità che p > q allora esisterà un b intero ovvero il più piccolo
intero positivo tale che:
Ovvero quindi moltiplicando per q, . Ma questo ci porta a dire che
, cioè √ dove b = 1, 2, 3, 4, 5, 6, ………. e q è un numero primo quindi un
numero dispari.
A questo punto possiamo considerare un rete di calcolatori e una serie di valori di b = 1, 2, 3, 4, ……100
Ogni calcolatore dovrà occuparsi di verificare i possibili divisori interi positivi e dispari
appartengono all’intervallo q di n che
dove e tutti i valori di b sono interi positivi. Ma
quanti valori di b dobbiamo considerare ? Di quanti computer avremo bisogno per attaccare un problema
RSA ? Difficile dirlo con esattezza ma possiamo fare un ragionamento statistico: possiamo calcolare il
rapporto k = p/q dei problemi RSA già risolti per verificare se è possibile assegnare a k un intervallo di
valori ristretto. L’esperienza mostra che normalmente p, q hanno lo stesso numero di cifre o comunque
non differiscono mai per più di tre cifre quindi è ragionevole pensare che b = 1, 2, 3, 4, ……1000 sia un
insieme sufficientemente ampio. Il costo computazione che dovrà affrontare ogni PC sarà pari a:
Per un costo totale di T = 1000*c
E’ comunque improbabile che p, q siano vicini alla √ perché in questo caso ~
√ e dall’equazione
ponendo il delta > 0
e risolvendo in x si arriverebbe presto alla soluzione. Ci si
concentrerà quindi su gli altri intervalli che l’algoritmo propone.
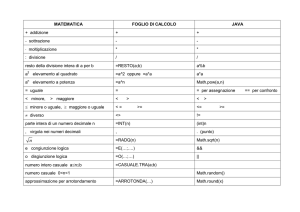
In ogni PC dovrà essere impiegato un software adatto a gestire grandi numeri come il PARI/GP, JAVA o il
Python che sono facilmente programmabili e gratuiti. Ovviamente questo algoritmo può fattorizzare
qualunque numero e non solo problemi RSA.
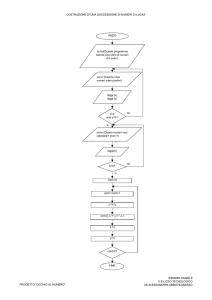
Un esempio di applicazione in Python per essere eseguita in un solo PC (quindi non in parallelo) potrebbe
essere:
def fattore(n):
import math;
b = 1;
while b < 200:
cont = 1;
k = math.ceil(math.sqrt(n/b));
while cont < 4000:
if math.fmod(n,k) == 0 and k != 1:
print(k);
print(n/k);
return("programma finito");
else:
k = k+1;
cont = cont +1;
b = b+1;
Osservazione importante
Dalla relazione √ e dal fatto che , 2√ deduciamo dopo facili passaggi
algebrici che √
√
2√ ovvero
√
√
√√
√!
√ per b > 1. Questa relazione ci fornisce un
intervallo più ristretto (ottimale) per la ricerca del fattore q una volta fissato b riducendo così il costo
computazionale unitario a:
√√
√
√ √
E sulla base di questa ultima considerazione il programma può essere così modificato:
def fattore(n):
import math;
b = 1;
while b < 200:
cont = 1;
k = math.ceil(math.sqrt(n/b));
w = math.ceil(math.sqrt(n*b)/(2*math.sqrt(b)-1));
while cont < w:
if math.fmod(n,k) == 0 and k != 1:
print(k);
print(n/k);
return("programma finito");
else:
k = k+1;
cont = cont +1;
b = b+1;