Autore con Marco Tarocco di
UbiMath Matematica per il tuo futuro Ed. Le Monnier 2014
Autore diel sito aperto UbiMath
www.ubimath.org se è importante quello che si insegna,
lo è ancora di più come lo si insegna…
Ubaldo Pernigo – 5 marzo 2014
Alcune linee guida
ß Metodo operativo e sperimentale
ß Partire da quanto possiedono gli alunni
ß Disegno come fondamentale accessorio della
geometria
ß Visualizzare e rappresentare come guida alla
risoluzione di problemi
Risorse a disposizione
⎥ Libri di testo
⎥ Ausili didattici «antichi»
†Riga e compasso
†Colori a matita e taglia incolla
†Cordicelle e carta
⎥ Ausili didattici «moderni»: software per la
matematica dinamica
Alcune idee operative verso
le competenze
ß Uso di strumenti e sperimentare
⎥ Quando si sperimenta creando delle figure si
forniscono agli allievi dimensioni indicative.
⎥ E’ importante disegnare senza vincoli. Questo, tra
l’altro, aiuta la successiva astrazione.
⎥ Le figure devono essere sempre abbastanza
grandi.
ß Uso della tecnologia
Riga e compasso, mostrare per
ricordare
ß La perplessità dei
tempi didattici
ß “… più tempo i nostri ragazzi avranno
dato allo studio del concreto, quanto
più tempo avranno perduto
nell’osservare, tanto meglio
passeranno dopo alla comprensione
delle forme astratte.”
(CASTELNUOVO E. , 1963. La
Didattica della Matematica. Firenze,
La Nuova Italia.)
Taglia incolla
ß Attività che coinvolge
ß Manipolare aiuta
ß Fantasia, creatività e
metodo, convivono e
coinvolgono
Utilità
ß Nella scuola secondaria di primo grado le
dimostrazioni formali non fanno parte del
percorso. Si passa dal caso specifico alla
generalizzazione.
ß Il ricorso allo sperimentare e a strumenti per
la matematica dinamica sono più significativi
di semplici e uniche figure statiche,
superando anche il libro di testo.
Ci vuole tempo…
ß Certo, ci vuole
tempo
ß Si lavora sul
supporto tra pari
ß Si lavora
discutendo e
affrontando
problemi
ß Si utilizza un
metodo aperto al
confronto
Il geopiano
Colorare
Realizzare modelli
Ruolo degli applicativi per la matematica dinamica
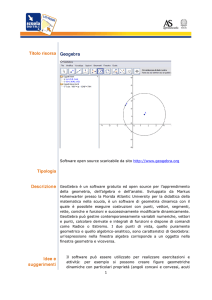
GeoGebra
ß GeoGebra è un software per l'apprendimento e
l’insegnamento della geometria, dell’algebra e
dell’analisi.
ß E’ uno strumento di geometria dinamica orientato
all’utilizzo didattico e all’apprendimento.
ß E’ uno strumento per l’algebra e l’analisi,
implementando la possibilità di inserire , per
esempio, direttamente equazioni.
ß Questi due aspetti sono intimamente legati,
proprio come dovrebbero essere visti dal docente e
dagli studenti.
come si presenta in 2D
come si presenta in 3D
perché usare GeoGebra
ß Open source e gratuito
ß Cross-­‐Platform
ß Strumento aperto
ß Cloud nativo
ß Comunità di aiuto reciproco
ß Nel solco delle Indicazioni
ß Dinamicità e flessibilità
ß Nativo per la LIM
ß BES e DSA
ß Supporto nei libri di testo
Open source e gratuito
ß Usabile liberamente dai docenti
ß Usabile liberamente dalle scuole
ß Usabile liberamente dagli studenti
ß Il fatto che si tratti di un prodotto gratuito
⎥ è importante per motivi economici
⎥ è importante perché diffonde una corretta cultura
relativa all'uso delle risorse per computer,
riducendo il fenomeno della pirateria informatica
ß Un progetto «lavora» e «cresce» a scuola e a
casa indifferentemente
cross-­‐platform
ß Disponibile su tutte le
piattaforme
⎥ Si può usare direttamente in
rete senza installazione e con il
vantaggio di avere sempre
l’ultima versione al lavoro. Per le
scuole è un’opportunità.
⎥ Lavora su tutte le piattaforme in
offline (scaricare e installare).
⎥ Tablet App.
ß www.geogebra.org/cms/it/download/
cloud GeoGebra nativo
ß GeoGebraTube è, dal 2011, il repository
ufficiale dei prodotti GeoGebra e dei prodotti
gratuiti (ottobre 2013, circa 47 000 prodotti).
⎥ La nuvola è condivisione
⎥ La nuvola è backup
⎥ La nuvola a scuola come raccolta ragionata
comunità di aiuto reciproco
ß Per qualsiasi problema, approfondimento su una
determinata funzione o strumento, su come realizzare una
costruzione geometrica facile o complessa, c’è sempre
qualcuno che può darci una mano.
ß www.geogebra.org/cms/it/community-­‐info
Utilizzo in contesto
ß L’uso della tecnologia deve essere mirato e
contestualizzato
ß Non deve essere sempre presente e non
sostituisce quaderno e gli usuali strumenti
Libri di testo e manuali
ß Presente
nei libri di
testo
ß Manuali e
videolezioni
on line di
qualità
Esercizi cmq usabili
nel solco delle Indicazioni
ß Le Indicazioni Nazionali fanno intravedere in
modo più o meno esplicito la presenza del
laboratorio di matematica come scelta
metodologica e non occasionale.
⎥ Scuola Secondaria di Secondo grado (2010)
†archivio.pubblica.istruzione.it/riforma_superiori/nu
ovesuperiori
⎥ Scuola Primaria e Secondaria di Primo grado
(2012, C.M. n. 22 del 26 agosto 2013)
†www.indicazioninazionali.it
dinamicità e flessibilità
ß La modifica di una delle rappresentazioni
geometriche o algebriche di una figura, forza
l’adattamento automatico delle altre per
mantenere le relazioni tra i diversi oggetti
ß GeoGebra è un software flessibile e può
essere usato sia per mostrare semplici
relazioni geometriche sia proprietà
geometriche complesse.
ß Rappresentazione bivalente, grafica e
algebrica, di un oggetto.
grafica superlativa
ß La grafica GeoGebra è assolutamente curata
e di effetto
ß La definizione dei dettagli è ottimale anche a
grande ingrandimento
ß Le convenzioni di scrittura sono da «libro» e si
può imparare facendo
pro e contro
ß GeoGebra e l’utilizzo di strumenti software trova anche
ß
ß
ß
ß
ß
ß
colleghi scettici
Non è in ogni modo un mezzo automatico di risoluzione di
problemi e questo deve essere chiaro agli allievi
Prima l’alunno deve pensare poi fare
L’uso di software didattici non è e non può essere la
soluzione ai problemi di insegnamento di geometria e di
algebra
Può essere un ottimo valore aggiunto per alcuni particolari
temi dell’insegnamento della geometria e dell’algebra
problem solving vs problem posing
La manualità e gli approcci tradizionali non devono essere
persi ma sono parte integrante di un percorso didattico
della geometria
riduzione dei tempi
didattici
ß Miglioramento la qualità dell’insegnamento
⎥ integrazione ottimale tra la didattica di classe e la
preparazione delle lezioni e dei materiali
ß Incremento della velocità di apprendimento
⎥ setting d’aula ridotto
ß Si creano circostanze favorevoli ad un
miglioramento delle presentazioni
ß Momenti di verifica innovativi
come si lavora
ß Ognuno deve poter provare
ß LIM guida
ß Schede
ß Preparare il
lavoro
ß La collaborazione tra pari è fondamentale
esempi e studi di caso
ß Costruzioni con riga e compasso, elastici,
geopiano, funicelle
ß Costruzioni con un programma per la
matematica dinamica
⎥ Costruire in vari modi un triangolo rettangolo
⎥ Costruibilità di un triangolo e classificazione in
base agli angoli
⎥ La somma degli angoli interni di un triangolo
⎥ Problemi di massimo nei triangoli
⎥ Punti notevoli del triangolo e retta di Eulero
Esempi
Costruzione per punti
Costruzione diretta
ß Costruzione diretta con lo strumento
poligono e controindicazioni
Attenzione ad alcune regole
ß I progettisti dei programmi per la matematica
dinamica fanno delle scelte e occorre
conoscerle e farne esperienza.
Costruzione dinamica
ß Mantiene il triangolo rettangolo.
Utilizzo di lati variabili
Linea di inserimento
Con una semicirconferenza
Esempi
Esempi
Esempi
Esempi
Massimo
Tra tutti i
triangoli aventi
la stessa base e
lo stesso
perimetro
trovare quello
di area
massima.
Minimo
Tra tutti i
triangoli di
data base e di
data area
trovare quello
di minimo
perimetro.
Internet è ricco di spunti per la didattica tradizionale
e a maggior ragione per le opportunità che le nuove tecnologie offrono
Novità 2014
Novità 2014
Novità 2014