ALGEBRA RELAZIONALE
Linguaggi per basi di dati
• I linguaggi per la interazione con DBMS sono una
componente fondamentale per le basi dati (sino
ad ora abbiamo solo visto SQL):
• operazioni sullo schema
• DDL: data definition language
• operazioni sui dati
• DML: data manipulation language
• interrogazione ("query")
• aggiornamento (inserimento, cancellazione, modifica)
2
1
Linguaggi di interrogazione
per basi di dati
• In base a come si specifica una
interrogazione, i Data Manipulation
Languages si dividono in:
• Dichiarativi
specificano le proprietà del risultato ("che
cosa")
• Procedurali
specificano le modalità di generazione del
risultato ("come")
3
Linguaggi di interrogazione per il
modello relazionale
• Algebra relazionale: procedurale
• Calcolo relazionale: dichiarativo (teorico)
• SQL (Structured Query Language):
parzialmente dichiarativo (reale)
• QBE (Query by Example):
dichiarativo (reale)
4
2
Algebra relazionale
• Costituito da un insieme di operatori
definiti su relazioni e che producono
relazioni come risultati
• Gli operatori possono essere composti in
cascata per formulare interrogazioni
complesse
5
Operatori dell'algebra relazionale
• Unione, intersezione, differenza (operatori
insiemistici)
• Ridenominazione, selezione, proiezione
(operatori monadici, agiscono su una sola
relazione)
• Join: join naturale, prodotto cartesiano,
theta-join (operatori su due o più relazioni)
6
3
Operatori insiemistici
• Dato che le istanze di relazioni sono insiemi ha
senso considerare gli operatori definiti per gli
insiemi
• Tuttavia una relazione nel modello relazionale
differisce da una generica relazione insiemistica
per la presenza dello schema
• Per evitare risultati non coerenti, l’applicazione
degli operatori unione, intersezione, differenza
deve essere limitata a relazioni definite sugli
stessi attributi
7
Unione
• L’unione tra due relazioni R1 ed R2 definite
sullo stesso insieme di attributi X è indicata
con R1 ∪ R2 ed è una relazione su X
contenente le n-uple che appartengono ad
R1 o ad R2 o ad entrambe
8
4
Unione
• Siccome in una relazione non possono
esserci due n-uple uguali, le n-uple che
sono presenti in entrambe le relazioni di
partenza vengono rappresentate una sola
volta nell’unione
9
Unione
Laureati
Quadri
Matricola Nome
7274
Rossi
7432
Neri
9824
Verdi
Età
42
54
45
Matricola Nome
9297
Neri
7432
Neri
9824
Verdi
Età
33
54
45
Laureati ∪ Quadri
Matricola Nome
7274
Rossi
7432
Neri
9824
Verdi
9297
Neri
Età
42
54
45
33
10
5
Unione
• Grado?
• Cardinalità?
Grado: inalterato
MAX(#(R1),#(R2)) ≤ #(R1 ∪ R2) ≤ #(R1) + #(R2)
11
Intersezione
• L’intersezione tra due relazioni R1 ed R2
definite sullo stesso insieme di attributi X è
indicata con R1 ∩ R2 ed è una relazione su
X contenente le n-uple che appartengono
sia ad R1 che ad R2
12
6
Intersezione
Laureati
Quadri
Matricola Nome
7274
Rossi
7432
Neri
9824
Verdi
Età
42
54
45
Matricola Nome
9297
Neri
7432
Neri
9824
Verdi
Età
33
54
45
Laureati ∩ Quadri
Matricola Nome
7432
Neri
9824
Verdi
Età
54
45
13
Intersezione
• Grado?
• Cardinalità?
Grado: inalterato
0 ≤ #(R1 ∩ R2) ≤ MIN(#(R1),#(R2))
14
7
Differenza
• La differenza tra una relazione R1 ed una
relazione R2 definite sullo stesso insieme di
attributi X è indicata con
R1 - R2 ed è una relazione su X contenente
le n-uple di R1 che non appartengono ad R2
• La differenza NON È commutativa
15
Differenza
Laureati
Quadri
Matricola Nome
7274
Rossi
7432
Neri
9824
Verdi
Età
42
54
45
Matricola Nome
9297
Neri
7432
Neri
9824
Verdi
Età
33
54
45
Laureati – Quadri
Matricola Nome
7274
Rossi
7432
Neri
9824
Verdi
Età
42
54
45
16
8
Differenza
• Grado?
• Cardinalità?
Grado: inalterato
0 ≤ #(R1 - R2) ≤ #(R1)
17
Operatori insiemistici e schemi
• Come applicare operatori insiemistici tra
relazioni definite su schemi diversi?
Paternità
Maternità
Padre
Adamo
Adamo
Abramo
Figlio
Abele
Caino
Isacco
Madre
Eva
Eva
Sara
Paternità ∪ Maternità
??
Figlio
Abele
Set
Isacco
18
9
Ridenominazione
• operatore monadico (con un argomento)
• "modifica lo schema" di una relazione cambiando
il nome di uno o più attributi e lasciando
inalterata l'istanza
• Data una relazione R definita su un insieme di
attributi X la ridenominazione di A⊆X in A’ si
indica con:
RENA’←A(R)
19
Paternità
Padre
Adamo
Adamo
Abramo
Figlio
Abele
Caino
Isacco
RENGenitore ← Padre (Paternità)
Genitore
Padre
Figlio
Adamo Abele
Adamo Caino
Abramo Isacco
20
10
RENGenitore ← Padre (Paternità)
Paternità
Padre
Adamo
Adamo
Abramo
Figlio
Abele
Caino
Isacco
RENGenitore ← Madre (Maternità)
Maternità
Madre
Eva
Eva
Sara
Genitore Figlio
Adamo Abele
Adamo Caino
Abramo Isacco
Figlio
Abele
Set
Isacco
Genitore Figlio
Eva
Abele
Eva
Set
Sara
Isacco
21
RENGenitore ← Padre (Paternità)
Genitore Figlio
Adamo Abele
Adamo Caino
Abramo Isacco
RENGenitore ← Padre (Paternità)
∪
RENGenitore ← Madre (Maternità)
RENGenitore ← Madre (Maternità)
Genitore Figlio
Eva
Abele
Eva
Set
Sara
Isacco
Genitore Figlio
Adamo Abele
Adamo Caino
Abramo Isacco
Eva
Abele
Eva
Set
Sara
Isacco
22
11
Impiegati Cognome Ufficio Stipendio
Rossi
Neri
Operai
Roma
Milano
Cognome Fabbrica
Bruni
Monza
Verdi
Latina
55
64
Salario
45
55
REN Sede, Retribuzione ← Ufficio, Stipendio (Impiegati)
∪
REN Sede, Retribuzione ← Fabbrica, Salario (Operai)
Cognome
Rossi
Neri
Bruni
Verdi
Sede Retribuzione
Roma
55
Milano
64
Monza
45
Latina
55
23
Ridenominazione
• Grado?
• Cardinalità?
Grado: inalterato
Cardinalità: inalterata
24
12
Ridenominazione
• Vincoli:
• Non si può assegnare ad un attributo un nome
che compare già come nome di un attributo
della relazione
25
Selezione
• operatore monadico
• produce un risultato che:
• ha lo stesso schema dell'operando
• contiene un sottoinsieme delle ennuple
dell'operando: quelle che soddisfano una
condizione si selezione
26
13
Selezione
• Una condizione di selezione su un insieme
di attributi X è una formula proposizionale
su X ottenuta combinando con i connettivi
logici AND(∨), OR(∧) e NOT(¬) condizioni
atomiche del tipo AχB o Aχc dove:
• χ è un operatore di confronto (=,<,>,…)
• A e B sono attributi di X su cui χ abbia senso
• c è una costante compatibile con il dominio di
A
27
Selezione, sintassi e semantica
• sintassi
SEL Condizione (Operando)
• Condizione: espressione booleana (come
quelle dei vincoli di ennupla)
• semantica
• il risultato contiene le ennuple dell'operando
che soddisfano la condizione
28
14
Impiegati
Matricola Cognome Filiale Stipendio
7309
Rossi
Roma
55
5998
Neri
Milano
64
9553
Milano
Milano
44
5698
Neri
Napoli
64
• impiegati che
• guadagnano più di 50
• guadagnano più di 50 e lavorano a Milano
• hanno lo stesso cognome della filiale presso cui
lavorano
29
• impiegati che guadagnano più di 50
Impiegati
Matricola Cognome Filiale Stipendio
7309
Rossi
Roma
55
5998
Neri
Milano
64
9553
5698
Milano
Neri
Milano
Napoli
44
64
5698
Neri
Napoli
64
SELStipendio > 50 (Impiegati)
30
15
• impiegati che guadagnano più di 50
e lavorano a Milano
Impiegati
Matricola Cognome Filiale Stipendio
7309
5998
Rossi
Neri
Milano
Roma
55
64
5998
Neri
Milano
64
9553
Milano
Milano
44
5698
Neri
Napoli
64
SELStipendio > 50 AND Filiale = 'Milano' (Impiegati)
31
• impiegati che hanno lo stesso nome della filiale presso
cui lavorano
Impiegati
Matricola Cognome Filiale Stipendio
7309
9553
Milano
Rossi
Milano
Roma
55
44
5998
Neri
Milano
64
9553
Milano
Milano
44
5698
Neri
Napoli
64
SEL Cognome = Filiale(Impiegati)
32
16
Selezione
• Grado?
• Cardinalità?
Grado: inalterato
0 ≤ #( SELF(R) ) ≤ #(R)
33
Selezione con valori nulli
Impiegati
Matricola Cognome Filiale
7309
Rossi
Roma
5998
Neri
Milano
9553
Bruni
Milano
Età
32
45
NULL
SEL Età > 40 (Impiegati)
• la formula proposizionale è FALSA per
quelle n-ple in cui qualcuno degli
34
attributi coinvolti ha valore nullo
17
Un risultato non desiderabile
∪ SEL Età≤30 (Persone)
≠
Persone
SEL Età>30 (Persone)
• Perché? Perché le selezioni vengono valutate
separatamente!
• Ma anche
SEL Età>30 ∨ Età≤30 (Persone)
≠ Persone
• Perché? Perché anche le condizioni atomiche vengono
valutate separatamente!
35
SEL Età > 40 (Impiegati)
• la condizione atomica è vera solo per
valori non nulli
• per riferirsi ai valori nulli esistono forme
apposite di condizioni:
IS NULL
IS NOT NULL
• Una soluzione alternativa è ricorrere all’uso
di una "logica a tre valori" (vero, falso,
sconosciuto)
36
18
• A questo punto:
SEL Età>30 (Persone) ∪
SEL Età≤30 (Persone)
(Persone)
=
SEL Età>30 ∨ Età≤30 ∨ Età IS NULL (Persone)
=
Persone
∪
SEL
Età IS NULL
37
Impiegati
Matricola Cognome Filiale
7309
5998
Rossi
Neri
Milano
Roma
5998
9553
Bruni
Neri
Milano
9553
Bruni
Milano
Età
32
45
NULL
45
NULL
SEL (Età > 40) OR (Età IS NULL) (Impiegati)
38
19
Selezione e proiezione
• operatori "ortogonali"
• selezione:
• decomposizione orizzontale
• proiezione:
• decomposizione verticale
39
selezione
proiezione
40
20
Proiezione
• operatore monadico
• produce un risultato che
• È definito su un sottoinsieme Y degli attributi
dell'operando
• contiene n-uple ottenute considerando i valori
su Y delle n-uple dell'operando
41
Proiezione, sintassi e semantica
• Data una relazione R(X) ed un insieme Y⊂X
la proiezione di R su Y si indica con
PROJY(R) ed è una relazione R’ definita su
Y e contenente le n-ple di R
considerandone solo i valori su Y:
PROJY(R) = {t[Y] | t∈R}
42
21
Impiegati
Matricola Cognome Filiale Stipendio
7309
Neri
Napoli
55
5998
Neri
Milano
64
9553
Rossi
Roma
44
5698
Rossi
Roma
64
• per tutti gli impiegati:
• matricola e cognome
• cognome e filiale
43
• matricola e cognome di tutti gli impiegati
Matricola Cognome Filiale Stipendio
7309
Neri
Napoli
55
5998
Neri
Milano
64
9553
Rossi
Roma
44
5698
Rossi
Roma
64
PROJ Matricola, Cognome (Impiegati)
44
22
Proiezione
• Grado?
• Cardinalità?
1 ≤ Grado(PROJY(R)) ≤ Grado(R)
1 ≤ #( PROJY(R) ) ≤ #(R)
45
• cognome e filiale di tutti gli impiegati
Matricola Cognome Filiale Stipendio
7309
Neri
Napoli
55
5998
Neri
Milano
64
9553
Rossi
Roma
44
5698
Rossi
Roma
64
PROJ Cognome, Filiale (Impiegati)
46
23
Cardinalità delle proiezioni
• una proiezione
• contiene al più tante ennuple quante
l'operando
• può contenerne di meno
• se X è una superchiave di R, allora
PROJX(R) contiene esattamente tante
ennuple quante R
47
Selezione e proiezione
• Combinando selezione e proiezione,
possiamo estrarre interessanti informazioni
da una relazione
48
24
•
matricola e cognome degli impiegati che guadagnano
più di 50
Matricola Cognome Filiale Stipendio
7309
Rossi
Roma
55
5998
Neri
Milano
64
9553
5698
Milano
Neri
Milano
Napoli
44
64
5698
Neri
Napoli
64
PROJMatricola,Cognome (SELStipendio > 50 (Impiegati) )
49
Join
• Combinando selezione e proiezione, possiamo
estrarre informazioni da una relazione
• Non possiamo però correlare informazioni
presenti in relazioni diverse
• Il JOIN è l'operatore dell'algebra relazionale che
permette di correlare dati in relazioni diverse
50
25
Join
• Quali esami ha superato Maria Rossi e con quale
votazione?
studenti Matricola Cognome
6554
Rossi
8765
Neri
9283
Verdi
3456
Rossi
esami
Matricola
3456
3456
9283
6554
Nome
Mario
Paolo
Luisa
Maria
Data di nascita
05/12/1978
03/11/1976
12/11/1979
01/02/1978
Voto
30
24
28
26
Corso
Analisi I
Chimica
Analisi I
Fisica
51
Join naturale
• operatore binario (generalizzabile)
• produce una relazione le cui righe sono
ottenute concatenando le tuple degli
operandi sulla base di valori uguali in
attributi con lo stesso nome
• Il risultato del JOIN è definito sull'unione
degli attributi degli operandi
52
26
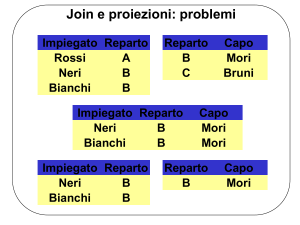
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparto
A
B
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Capo
Mori
Bruni
Capo
Mori
Bruni
Bruni
53
Join, sintassi e semantica
• R1(X1), R2(X2)
• R1 JOIN R2 è una relazione su X1∪X2
R1
JOIN
R2 = { t su X1 ∪ X2 | ∃ t1∈R1e t2∈R2
con t[X1] =t1 e t[X2] =t2 }
54
27
JOIN Completo
• Se ogni n-pla delle due relazioni
contribuisce al risultato il JOIN si dice
completo
• Altrimenti il join è non competo
55
Un join non completo
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparto
B
C
Impiegato Reparto
Neri
B
Bianchi
B
Capo
Mori
Bruni
Capo
Mori
Mori
56
28
JOIN vuoto
• Un caso particolare del JOIN non completo
è il JOIN vuoto che dà come risultato la
relazione vuota
57
Un join vuoto
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparto
D
C
Impiegato Reparto
Capo
Mori
Bruni
Capo
58
29
JOIN completo
• Il JOIN è completo se ogni n-upla delle due
relazioni si combina con ALMENO UNA nupla dell’altra relazione
• Un caso particolare di JOIN completo è
quello in cui ogni n-upla delle due relazioni
si combina con TUTTE le n-uple dell’altra
relazione
59
Un join completo, con n x m
ennuple
Impiegato Reparto
Rossi
A
B
Neri
B
Reparto
A
B
B
Impiegato Reparto
Rossi
B
Rossi
B
Neri
B
Bianchi
B
Capo
Mori
Bruni
Capo
Mori
Bruni
Mori
Bruni
60
30
Cardinalità del JOIN
• Il join di R1 e R2 contiene un numero di nple compreso fra zero e il prodotto di |R1|
e |R2|
• Il fatto che il JOIN sia completo non
significa che |R1 JOIN R2| = |R1|*|R2|
61
Cardinalità del JOIN
• se il join coinvolge una chiave di R2, allora …
il numero di n-ple è compreso fra zero e |R1| perché ciascuna n-upla
della prima relazione potrà combinarsi al più con una sola n-upla
della seconda
• se il join coinvolge una chiave di R2 e un vincolo
di integrità referenziale tra la chiave di R2 ed R1,
allora …
il numero di n-ple è pari a |R1| perché oltre a valere la condizione
precedente, ciascuna n-upla della prima relazione dovrà combinarsi
R2
R1
almeno con una n-upla della seconda
X
X
62
31
Cardinalità del join, esempi
R1(A,B) JOIN R2 (B,C)
• in generale
0 ≤ |R1 JOIN R2| ≤ |R1| × |R2|
• se B è chiave in R2
0 ≤ |R1 JOIN R2| ≤ |R1|
• se B è chiave in R2 ed esiste vincolo di integrità
referenziale fra B in R1 e R2:
|R1 JOIN R2| = |R1|
63
Proprietà del JOIN
• Il JOIN naturale soddisfa le proprietà:
• Commutativa:
R1
JOIN
R2 = R2
JOIN
R1
• Associativa:
R1
JOIN
R2
JOIN
R3 = (R1
JOIN
R2)
JOIN
R3 = R1
JOIN
(R2
JOIN
R3)
64
32
Join, una difficoltà
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparto
B
C
Capo
Mori
Bruni
Impiegato Reparto Capo
Neri
B
Mori
Bianchi
B
Mori
• Se il JOIN non è completo alcune n-ple non
contribuiscono al risultato: l’informazione nel
risultato non contiene alcune delle informazioni
65
negli operandi
Join esterno
• Il join esterno estende, con valori nulli, le
ennuple che verrebbero tagliate fuori da un
join (interno)
• esiste in tre versioni:
• sinistro, destro, completo
66
33
Join esterno
• sinistro: mantiene tutte le ennuple del primo
operando, estendendole con valori nulli, se
necessario
• destro: ... del secondo operando ...
• completo: … di entrambi gli operandi ...
67
Impiegati
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparti
Reparto
B
C
Capo
Mori
Bruni
Impiegati JOINLEFT Reparti
Impiegato Reparto
Neri
B
Bianchi
B
Rossi
A
Capo
Mori
Mori
NULL
68
34
Impiegati
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparti
Reparto
B
C
Capo
Mori
Bruni
Impiegati JOINRIGHT Reparti
Impiegato Reparto
Neri
B
Bianchi
B
NULL
C
Capo
Mori
Mori
Bruni
69
Impiegati
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparti
Reparto
B
C
Capo
Mori
Bruni
Impiegati JOINFULL Reparti
Impiegato Reparto
Neri
B
Bianchi
B
Rossi
A
NULL
C
Capo
Mori
Mori
NULL
Bruni
70
35
Cardinalità JOIN esterno
• La cardinalità minima, da 0 diventa:
• |R1| per il LEFT join
• |R2| per il RIGHT join
• MAX(|R1|, |R2|) per il FULL join
71
JOIN e proiezioni
• Date due relazioni R1(X1) ed R2(X2) si ha
che
PROJX1(R1 JOIN R2) ⊆ R1
• Infatti, nel caso che il JOIN non sia
completo, al risultato potrebbe partecipare
solo un sottoinsieme delle n-ple di R1.
72
36
Join e proiezioni
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparto
B
C
Impiegato Reparto
Neri
B
Bianchi
B
Impiegato Reparto
Neri
B
Bianchi
B
Capo
Mori
Bruni
Capo
Mori
Mori
Reparto
B
Capo
Mori
73
JOIN e proiezioni
• Data una relazione R(X) con X = X1∪X2 si
ha che:
(PROJX1(R)) JOIN (PROJX2 (R)) ⊇ R
• Si ha il segno = solo nel caso in cui …
X1∩X2 è una superchiave per R
74
37
Proiezioni e join
Impiegato Reparto
Capo
Neri
B
Mori
Bianchi
B
Bruni
Verdi
A
Bini
Impiegato Reparto
Reparto
Capo
Neri
B
B
Mori
Bianchi
B
B
Bruni
Verdi
A
A
Bini
Impiegato
Neri
Bianchi
Neri
Bianchi
Verdi
Reparto
B
B
B
B
A
Capo
Mori
Bruni
Bruni
Mori
Bini
75
Join e proiezioni
• R 1(X1), R 2(X2)
PROJX (R 1 JOIN R2 ) ⊆ R 1
1
• R(X), X = X1 ∪ X2
(PROJX1 (R)) JOIN (PROJX2 (R)) ⊇ R
76
38
Prodotto cartesiano
• Che succede se eseguo un join naturale tra relazioni
che non hanno attributi in comune?
• Ogni n-pla della prima relazione può combinarsi con
ognuna delle n-ple della seconda
• Il risultato contiene sempre un numero di n-ple pari al
prodotto delle cardinalità degli operandi
• In questo caso il JOIN diventa il prodotto cartesiano
tra i due operandi
77
Impiegati
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparti
Codice
A
B
Capo
Mori
Bruni
Impiegati JOIN Reparti
Impiegato Reparto Codice
Rossi
A
A
Rossi
A
B
Neri
B
A
Neri
B
B
Bianchi
B
A
Bianchi
B
B
Capo
Mori
Bruni
Mori
Bruni
Mori
Bruni
78
39
• Il prodotto cartesiano, in pratica, ha senso
solo se seguito da selezione:
SELCondizione (R1 JOIN R2)
• L'operazione viene chiamata theta-join e
indicata con
R1 JOINCondizione R2
79
Perché "theta-join"?
• La condizione C è spesso una congiunzione
(AND) di atomi di confronto A1ϑ A2 dove ϑ è uno
degli operatori di confronto (=, >, <, …)
• se l'operatore è sempre l'uguaglianza (=) allora si
parla di equi-join
80
40
Impiegati
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparti
Codice
A
B
Capo
Mori
Bruni
Impiegati JOINReparto=Codice Reparti
Impiegato Reparto Codice
Rossi
A
A
Rossi
A
B
Neri
B
Neri
A
Bianchi
B
B
Neri
B
B
Bianchi
B
A
Bianchi
B
B
Capo
Mori
Bruni
Mori
Bruni
Bruni
Mori
Bruni
81
Impiegati
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Reparti
Reparto
A
B
Capo
Mori
Bruni
Impiegati JOIN Reparti
Impiegato Reparto
Rossi
A
Neri
B
Bianchi
B
Capo
Mori
Bruni
Bruni
82
41
JOIN naturale ed equi-join
• Il JOIN naturale può essere ottenuto per
mezzo di operatori di ridenominazione,
equi-join e proiezione
83
Join naturale ed equi-join
Impiegati
Reparti
Impiegato Reparto
Reparto
Capo
Impiegati JOINnat Reparti =
PROJImpiegato,Reparto,Capo (
Impiegati JOINReparto=Codice RENCodice ← Reparto (Reparti)
)
84
42
JOIN e vincoli di integrità
referenziale
• Il vincolo di IR esplicita un legame tra gli
attributi di due tabelle diverse.
• Livello sintattico: valori della tabella interna
sono vincolati a comparire nella tabella
esterna
• Livello semantico: equi join tra attributi
interessati a vincolo IR esplicita
un’informazione non presente né in R1 né in
R2 se prese separatamente
85
JOIN e vincoli di integrità
referenziale
• Esempio: Lo schema sotto riportato rappresenta
informazioni sui dipendenti di un’azienda. Ogni
dipendente è affiliato ad un dipartimento. Ogni
dipartimento ha un direttore che è uno dei dipendenti
Dipendente(matricola, nome, cognome, dipartimento, stipendio)
Dipartimento(codice, descrizione, direttore)
• Quale informazione è resa esplicita da
Dipendente JOINdipartimento=codice Dipartimento
• Quale informazione è resa esplicita da
Dipendente JOINdirettore=matricola Dipartimento
86
43
JOIN e vincoli di integrità
referenziale
Dipendente JOINdipartimento=codice Dipartimento
Restituisce una tabella con una riga per ciascun
dipendente. Ogni riga esplicita i dati del dipendente e
quelli del dipartimento a cui il dipendente è affiliato
Dipendente JOINdirettore=matricola Dipartimento
Restituisce una tabella con una riga per ciascun
dipartimento. Ogni riga esplicita i dati del dipartimento e
quelli del dipendente che ne è direttore
87
Esempi
Impiegati Matricola Nome
Età Stipendio
Rossi
34
45
Bianchi 37
38
Neri
42
35
Bruni
43
42
Mori
45
50
Lupi
46
60
Supervisione Impiegato Capo
7309
5698
5998
5698
9553
4076
5698
4076
4076
8123
7309
5998
9553
5698
4076
8123
88
44
Esempi
•
•
•
•
•
•
Matricola, nome, età e stipendio degli impiegati che guadagnano più di 40
milioni
Matricola, nome ed età degli impiegati che guadagnano più di 40 milioni
Matricole dei capi degli impiegati che guadagnano più di 40 milioni
Nome e stipendio dei capi degli impiegati che guadagnano più di 40 milioni
Impiegati che guadagnano più del proprio capo, mostrando matricola, nome
e stipendio dell'impiegato e del capo
Matricole dei capi i cui impiegati guadagnano tutti più di 40 milioni
Impiegati
Supervisione
Impiegato
7309
5998
9553
5698
4076
Capo
5698
5698
4076
4076
8123
Matricola Nome
7309
Rossi
5998
Bianchi
9553
Neri
5698
Bruni
4076
Mori
8123
Lupi
Età
34
37
42
43
45
46
Stipendio
45
38
35
42
50
89 60
Esercizi
• Estrarre Nome e Cognome degli studenti lavoratori
• Nome e Cognome degli studenti NON lavoratori
• Nome e cognome degli studenti lavoratori che hanno sostenuto almeno un
esame con più di 4 crediti
• Nome e Cognome degli studenti che hanno preso almeno un trenta e mai un
voto inferiore a 27
• Nome e Cognome degli studenti che hanno dato Analisi I e non Geometria
• Nome e Cognome degli studenti che hanno dato almeno due esami
• Nome e Cognome degli studenti che hanno dato almeno due esami con lo
stesso docente
Studenti
Matricola
Corsi
Codice
Nome
Nome
Cognome Eta
Crediti
Docente
Esami
Corso
StudentiLavoratori
Matricola
Studente
Voto
Data
107
45