Università degli Studi di Cassino
Anno accademico 2003-2004
Corsi di Statistica 1, II (Prof. G. Prozio) e Statistica 1, IV (Dott. D. Vistocco)
Esercitazione del 23/2/2004
Dott. Claudio Conversano
Svolgimento
Poiché la cilindrata è misurata in cm3 è possibile considerare la radice terza della variabile
Cilindrata. I risultati relativi alle misure di associazione lineare restano invariati poiché si tratta di
un semplice cambiamento di scala.
La radice terza dei valori della variabile “Cilindrata” da luogo alla seguente distribuzione:
Cilindrata 8,89 9,62 10,35 10,75 14,36 10,6 13,56 17,07
Cilindrata
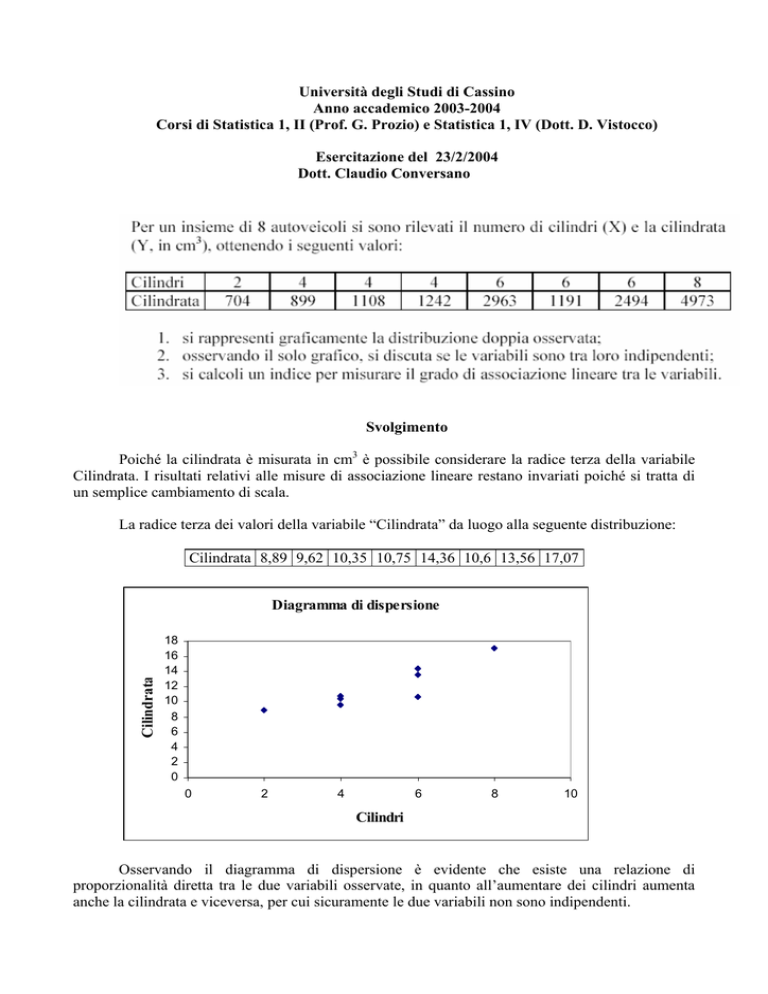
Diagramma di dispersione
18
16
14
12
10
8
6
4
2
0
0
2
4
6
8
10
Cilindri
Osservando il diagramma di dispersione è evidente che esiste una relazione di
proporzionalità diretta tra le due variabili osservate, in quanto all’aumentare dei cilindri aumenta
anche la cilindrata e viceversa, per cui sicuramente le due variabili non sono indipendenti.
Cilindri
(X)
2
4
4
4
6
6
6
8
40
Cilindrata
(Y)
8,89
9,62
10,35
10,75
14,36
10,6
13,56
17,07
95,2
µx =
µy =
1
n
xy
x
17,78
38,48
41,4
43
86,16
63,6
81,36
136,56
508,34
∑
xi =
2
y2
4
16
16
16
36
36
36
64
224
79,0321
92,5444
107,1225
115,5625
206,2096
112,36
183,8736
291,3849
1188,09
1
40 = 5
8
1
1
y
=
95 , 2 =11,9
∑
i
n
8
1
=
n
1
µ xy
∑ x i y i = 8 508 ,34 = 63 ,54
σ xy = µ xy − µ x µ y = 63,54 − (5 ⋅ 11,9) = 4,04
µ
x2
µy
2
1
=
n
1
=
n
∑
∑
yi
xi
2
2
1
=
224 = 28
8
1
= 1188 , 09 = 148 ,51
8
ρ =
=
1
n
1
n
(28
∑
x
∑
2
i
xi yi − µ x µ
−µ
2
x
1
n
∑
4 , 04
−5
2
)(148 , 51 − 11 , 9 )
2
y
y i2 − µ
2
y
= 0 , 888
=