MIRANDOLA 4 NOVEMBRE 2016
Intervento di Elisa Guagenti:
“Modelli probabilistici di pericolosità sismica- Quanto sono credibili?”
Questo intervento è un azzardo: non proietto immagini, parlo di matematica, e ho la pretesa di
interessare.
Che cosa mi propongo? Parlare di rischio sismico, naturalmente. Invitare a riflettere sul significato
della parola e della formula matematica coinvolte nell’argomento: capirne le insidie quando sono
esposte in modo nebuloso, saggiarne l’efficacia quando sono chiaramente esplicitate. Voglio
invitare a riflettere sul peso delle parole e sul significato delle formule.
Troppo spesso si sente dire: matematicamente certo. Parole pericolose. Ascoltiamo da subito le
parole di Einstein: “So far as the laws of mathematics refer to reality, they are not certain” (per quel
che riguarda l’applicazione alla realtà, le leggi della matematica non esprimono certezze).
Voglio con questo far dubitare della matematica? Mai più. Invece, proprio al suo metodo vogliamo
attingere, metodo che è di analisi rigorosa, per indagare quale sia il valore conoscitivo delle sue
affermazioni quando si applica alla realtà. Per COMPRENDERE.
Un modo di procedere che è anche importante, e molto, per non cadere nella bagarre dei SÍ e dei
NO. Astiose posizioni contrapposte cui troppo spesso ci capita di assistere. Non si tratta solo di
estetica (sono anche brutte) o di etica (sono anche cattive a volte): si devono prendere decisioni . E
si arriva a dei NO non argomentati, a dei SÍ non capiti.
Veniamo alle nostre parole. Comincio dalla prima parola contenuta nel titolo.
Modello (matematico): c’entra con il consueto significato di modello? Sì, un modello serve per
farsi un’idea del reale, per fare delle prove su di esso, per prevedere quel che potrebbe succedere.
Voglio commentare un’equazione ben nota: l’equazione di Newton F = ma (forza uguale a massa
per accelerazione). Alcuni studiosi la citano come primo esempio di modello matematico
Ma come? Siamo abituati a chiamarla legge, anzi legge fondamentale della dinamica.
Sì sì, continuiamo a chiamarla legge, ma è anche un primo esempio di modello in quanto
strumento di prova. Anche prima si sapevano tante cose; addirittura Keplero aveva scoperto le leggi
secondo cui si muovono i pianeti. Ma si trattava di descrizione; non c’era lo strumento dato
dall’equazione. Con essa si fanno prove e si progetta: cosa cambia al cambiare della forza, come
deve essere la traiettoria per una data forza, o al contrario come dimensionare la forza per una data
traiettoria…; progettiamo, appunto.
Ma una domanda si pone, importantissima. È certa questa legge? Beh, dopo aver dominato per 4
secoli come verità (con la V maiuscola), proprio Einstein ha capito che anche lei ha i suoi limiti di
validità. Limiti che sono ben vasti e facciamo bene a lasciarle il nome di legge. Ma una validità
assoluta non ce l’ha. La buttiamo via? Ce ne guardiamo bene! Funziona benissimo a tutt’oggi. Ce
la teniamo ben cara. Fa funzionare le macchine, ci racconta il moto dei pianeti, insomma domina a
tutt’oggi la dinamica. Ma, per indagare l’infinitamente piccolo o le velocità prossime a quelle della
luce, abbiam capito che trova i suoi limiti. Non diremo che una legge è vera, ma che rappresenta la
realtà entro confini e approssimazioni ben definiti. Questo è importante e bisogna esserne
consapevoli se vogliamo non prendere cantonate. E questo non per un puro compiacimento
intellettuale (perlomeno non solo: è anche importante una chiarezza di pensiero in sè). Ma
soprattutto perché, ripeto, poi si prendono decisioni e quelle sì che riguardano la realtà.
Quindi, la riflessione sul significato di una formula ci porta a comprenderne l’utilità e la relatività
nello stesso tempo: la STORICIZZIAMO.
Allora le definizioni, le delimitazioni danno significati nuovi a conoscenze acquisite. Conoscenze
sempre in divenire. Man mano che il mondo esplorato con metodi matematici si fa più complesso,
se perfino la legge fondamentale ha dovuto riconoscere i suoi limiti, ci siamo fatti più prudenti.
Nasce il più modesto nome di modello (anziché legge o teoria), quasi dichiarando in partenza che
dovremo proseguire e migliorarlo. La ricerca scientifica è bello vederla così, come storia di un
cammino comune che non butta via il passato ma ne precisa una nuova validità, procede con
consapevolezza più critica, acquisendo gradi di conoscenza in campi sempre più vasti.
Ne consegue anche una enorme responsabilità della scienza. E dell’insegnamento scientifico, che
sommamente può formare in modo critico e costruttivo al contempo. Non dobbiamo incamerare
acriticamente regole, ma capirne potenzialità e limiti. Non mai certezze assolute. E un altro aspetto
prezioso dell’insegnamento scientifico è la precisione del linguaggio: quando dico a parole forza,
massa, accelerazione le ho ben definite. Ci intendiamo quando parliamo.
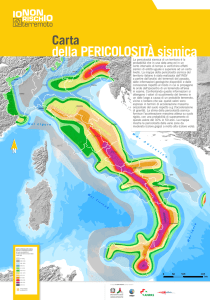
Veniamo ai terremoti. In che cosa consiste un modello di pericolosità sismica?
Basandosi su studi sismologici, geofisici e sulla storia catalogata degli eventi sismici si arriva a
individuare dove siano le faglie, come possa accadere che l’energia accumulata diventi così grande
che lungo di esse le rocce non riescono a rimanere aderenti fra loro per attrito e scorrono
improvvisamente, cioè avviene il terremoto. Non solo, si valuta il tempo di accumulazione di tale
energia, si studiano i cataloghi. Si arriva così a definire un periodo di ritorno dei terremoti di diverse
intensità definite secondo scale che abbiamo imparato a conoscere; periodo di ritorno che non
significa che sappiamo ogni quanti anni capita il terremoto in quella zona, ma una media sul lungo
periodo e una tendenza nel medio periodo sì. Infine si sa come si propagano le onde sismiche e
quanto arriva in un sito specifico in termini di accelerazione al suolo, grandezza che è la principale
caratteristica locale in base alla quale si dovrà infine progettare la costruzione che al terremoto
dovrà resistere.
Si può ben capire che non si tratta di un modello semplice che si esprima in nitide equazioni.
Si arriva a individuare non, con esattezza, dove quando con che intensità si verificherà il terremoto;
ma, con incertezze, zone, periodi di tempi di maggior pericolo, e quale range di intensità aspettarsi.
Si costruisce un modello di previsione probabilistica (secondo termine contenuto nel titolo…)
Ma allora? Com’è che abbiamo tanto sentito dire che i terremoti non si possono prevedere?
Altra occasione per pesare le parole. Riflettiamo su quell’innocente SI PUÒ.
Se affermo che due rette parallele non possono incontrarsi, chi ha studiato qualcosa di geometrie
non euclidee mi direbbe “ dipende”, in quale geometria ragioniamo. O che 1+1 non può fare che 2,
mi direbbe “dipende” in quale algebra. O ancora, che il baricentro è quel punto dove si può
applicare il peso totale (è una risposta tipica di studenti poco riflessivi), dipende: se vogliamo
calcolare anche solo la fatica di alzare un braccio capiamo che non è così. Non faremmo nessuna
fatica se il peso si potesse applicare nel baricentro.
Morale, sul significato del “si può” dobbiamo essere esigenti: va corredato dal campo di
applicabilità e dallo strumento utilizzabile. Per non accontentarci di pseudospiegazioni.
Se perfino la legge fondamentale della dinamica va affermata nei limiti della sua validità, così
parrebbe anche per la prevedibilità dei terremoti che, con le conoscenze attuali, non sappiamo
definire nel loro verificarsi dove, quando e con quale intensità, ma di cui, sempre con le conoscenze
attuali, sappiamo valutare la probabilità. Allora l’affermazione va espressa correttamente nei suoi
limiti “i terremoti non si possono prevedere in senso deterministico, si possono prevedere in
senso probabilistico”. Non escludendo (anzi aiutandosi con) conoscenze espresse in senso
deterministico: si conoscono le faglie, si misura l’energia liberata, si definiscono zone e periodi di
maggior pericolo… Ma tutto con incertezza e l’incertezza è misurata dalle probabilità.
Concetto con cui purtroppo abbiamo ancora poca dimestichezza, abituati come siamo alla logica
deterministica che ancora domina la nostra formazione scientifica. E si capisce: un poco sgomenta
non avere risposte certe alle nostre domande. La probabilità non risponde con un sì o con un no. Ci
mostra il panorama delle aspettative, basato sulle conoscenze fino al momento conseguite.
Aspettative quindi, e non una volta per tutte, ma aggiornantesi man mano che nuove conoscenze
saranno acquisite.
Ma che cos’è questa probabilità, termine che ho introdotto di soppiatto, come sinonimo di
incertezza? È un numero, fra zero e uno, che misura l’aspettativa di un evento. Dobbiamo
accontentarci di essere consapevoli dell’incertezza, punto e stop?
Esiste una, lasciatemi dire, bellissima formula matematica che governa il calcolo delle probabilità.
È stata formulata da un monaco matematico del ‘700, Thomas Bayes, lasciata poi nell’oblio,
riproposta come strumento fondamentale solo nel secolo scorso, soprattutto per merito di un nostro
grandissimo matematico italiano, Bruno de Finetti.
Si scrive:
|
∙
|
⁄
Si legge:
La P di una
ipotesi H,
data una
evidenza E
La P di H,
a priori
Un fattore di
verosimiglianza
Solo oggi è stata veramente capita (altra occasione per riflettere sul faticoso ma esaltante cammino
del nostro sapere), come chiave di volta per esprimere l’acquisizione di conoscenza e per vagliarne
il grado di attendibilità.
Non l’ho mostrata, ovviamente, per spiegarla. Ma per intuire come, nella formulazione matematica,
possa essere ospitato il nostro stesso modo di apprendere: dapprima ci facciamo un’idea su di un
fenomeno (probabilità a priori), poi, man mano che accumuliamo esperienze, la nostra
comprensione si precisa e si affina (probabilità a posteriori).
La mostro anche per invitare a capire le formule matematiche, non solo mandarle a memoria. Nel
caso della previsione dei terremoti significa: dapprima si ha un certo grado di aspettativa; dopo il
verificarsi di un altro evento, che si pensa correlato, la nostra aspettativa cambia, in dipendenza
dalla congettura iniziale e dai fatti osservati.
È proprio questa formula che sostiene la previsione a breve termine (quella che è possibile,
probabilisticamente). Ci sono dei fenomeni che da secoli, si sa, A VOLTE precedono terremoti
violenti: ad esempio le scosse medio-deboli, che, appunto si chiamano precursori. Però ciò accade
solo a volte. Che me ne faccio di una affermazione così blanda? La gente lo sa cosa farsene e
scappa fuori casa. Il calcolo delle probabilità esprime questa preoccupazione nella formula che ho
mostrato. Cosa ci dice? Calcola la probabilità di un terremoto violento nei prossimi giorni, dato il
verificarsi del precursore. Per esempio una zona che sia esposta a un terremoto violento con periodo
di ritorno di 50 anni, la probabilità (a priori) di terremoto nei prossimi 3-4 giorni, in assenza di
precursori, è piccolissima, 0.0002. Qualora si verifichi il precursore la probabilità (a posteriori) è
0.02, che è sempre piccola, ma 100 volte maggiore. Di più, se si verificasse un secondo precursore
(sono allo studio diversi fenomeni candidati precursori: l’emissione anomala di gas radon,
variazioni del campo elettromagnetico…), la probabilità a posteriori diverrebbe altissima, più del
60%.
Tutto chiaro? Mica tanto. Conoscenza fisica, storia sismica, formula di Bayes guidano il calcolo
probabilistico. Il guaio è che non lo determinano in modo univoco, cosicché accade che i modelli di
pericolosità sismica possono differire fra loro e condurre a valori di probabilità anche molto diversi
fra loro.
E qui di nuovo il pericolo della contrapposizione sì/no, va bene il mio non va bene il tuo. Ciascuno
sfoggia criteri di validità, che assoluti non sono.
E allora? Dobbiamo scoraggiarci?
Dice Imre Lakatos (uno scienziato che è anche un eminente epistemologo): “ogni nostra teoria è
nata in un mare di anomalie”. Ma poi la conoscenza è cresciuta, le incertezze sono diminuite, i
risultati sono andati convergendo. Il processo è lungo, ci vuole tenacia, umiltà, fiducia reciproca,
argomentazioni attente, ascolto e confronto. Sembrerà strano: sembrano categorie morali piuttosto
che scientifiche. Sono indispensabili, in entrambi i campi.
Ho avuto il privilegio di condividere vita e studi con Giuseppe Grandori. I pensieri che ora espongo
sono suoi.
Specialmente a partire dagli anni ‘90 GG ha dedicato molto dei suoi pensieri sul come diminuire le
incertezze, abbandonando pretese di verità, ma convinto di poterne districare il groviglio. Sentiva
moltissimo la responsabilità delle decisioni da prendere: che fossero le migliori possibili. Vale ogni
sforzo per sceglier nel modo migliore, sia pur in senso relativo, sfruttando al massimo tutte le
conoscenze disponibili.
Leggiamo le sue parole. Dice G. Grandori: “A volte è stato suggerito di usare un certo numero di
modelli (farne una specie di media) e poi adottare come misura dell’incertezza un coefficiente di
variazione inteso a includere sia le incertezze statistiche che di modellazione. Questo modo di
procedere deve essere pazientemente ma fermamente confutato e scoraggiato. […….] la procedura
è formalmente non corretta.”
La prima pubblicazione di Giuseppe Grandori in merito porta il titolo “Paradigms and falsification
in Earthquake Engineering” e reca questa argomentazione (che traduco): “A proposito della
valutazione di hazard, in particolare dell’intensità di un terremoto con periodo di ritorno di 500
anni, mantengo la mia affermazione che essa sia, in linea di principio, falsificabile; ma, per
condurre un esperimento a tal fine, occorrerebbero migliaia di anni. Perciò, in pratica, non è
falsificabile. Per superare tale ostacolo propongo di spostare all’indietro l’attenzione: dai risultati
finali del calcolo, che non sono direttamente falsificabili, alla procedura del modello che li ha
prodotti.”
Con ciò siamo ancora al punto cruciale dell’intento che, come dicevo all’inizio, mi propongo.
Riflettere sul significato della parola e della formula matematica, in particolare quando modella
fenomeni reali. L’importanza della procedura con cui si ottengono i risultati! Quali variabili si son
tenute in conto, quali confronti eseguiti, quali considerazioni di contesto…. In una parola, il
Metodo!
Ma come si fa a controllare il metodo?
Tipico del procedere di Grandori è la attenta analisi teorica, sempre per arrivare, da ingegnere nel
senso più alto, a una tecnica operativa per decidere: come agire, e soprattutto come agire
correttamente in senso complessivo, tecnico e sociale. Ma proprio per questo, per decidere bene in
questo mare di incertezze ha dovuto aggredire anche un campo altamente teorico, il campo
dell’epistemologia. Su questo non mi addentro perché ci vorrebbe una lezione specifica, ma ne
voglio informare. GG ha introdotto il concetto di credibilità di un modello (ultima parola del titolo)
e ha costruito un metodo di confronto fra modelli, qualora conducano a probabilità diverse fra loro,
per decidere quale sia migliore, a seconda della grandezza che si voglia stimare. Metodo che, lungi
dall’essere litigioso, guida in modo chiaramente esplicitabile a decisioni giustificate.
Abbiamo parlato fin qui di pericolosità sismica. La probabilità entra di prepotenza per guidarci nella
sua stima. Ancor più specificamente è insita nel concetto di rischio. Il rischio è, in generale, per
definizione stessa, una probabilità: la probabilità di subire un certo danno da parte di un sistema
che, per quanto in buona salute o ben costruito, ha un certo grado di resistenza, non infinita, a quella
pericolosità.
Per fortuna, il comportamento strutturale degli edifici è ben più conosciuto del comportamento di
generazione dei terremoti. Perciò il rischio residuo, ineliminabile concettualmente dal progetto, è
veramente molto piccolo per le costruzioni nuove, ben progettate secondo la normativa sismica.
Infine la domanda centrale di questo convegno: a che scopo si dovrebbe essere consapevoli del
rischio sismico?
Qualcosa di più che una miglior convivenza con il terremoto.
È infatti diventata emblematica, a livello internazionale, la domanda “Who shall decide?”. La
ricerca più avanzata argomenta come e perché i cittadini, correttamente informati, debbano essere
coinvolti nelle decisioni. Perché le decisioni si prendono, le normative vengono scritte, i cittadini ne
vivono le conseguenze.
È giusto, allora, che partecipino alle decisioni. L’intervento del prof. Allegretti sarà specifico
sull’argomento. Intanto voglio leggere parole di GG sull’argomento: “il compito del decisore è
molto delicato. Egli deve utilizzare con metodo trasparente le più aggiornate conoscenze
confrontandosi con la cittadinanza. È suo compito coinvolgere la cittadinanza spiegando quale sia il
livello di rischio e discutendo i possibili livelli di intervento e infine motivando una SCELTA
DECISIONALE. Solo in tal modo la scelta del decisore potrà essere capita e condivisa”.
Ma è possibile argomentare su temi scientifici che sono sul fronte della ricerca? Un tentativo in
questo senso è quel che stiamo facendo oggi, insieme.