Circuiti elettronici per il trattamento dei segnali

Circuiti elettronici per il trattamento dei segnali
In elettronica , il sample and hold (abbreviato S&H) viene utilizzato come interfaccia con il
mondo reale, convertendo segnali analogici al dispositivo seguente, come ad esempio un
convertitore analogico/digitale o ADC. L'effetto di questo circuito è di mantenere il valore
analogico costante per il tempo necessario al convertitore o ad altri circuiti successivi per compiere
delle operazioni sul segnale.
Nella maggior parte dei circuiti si utilizza un condensatore a bassa capacità C per conservare la
tensione analogica, più un transistor (solitamente un MOSFET, che ha una piccola resistenza di
ingresso intrinseca R), il quale funge da interruttore, connettendo e disconnettendo il condensatore
all'ingresso analogico. Al source del transistor è collegato un buffer , che mantiene l'impedenza di
ingresso globale elevata.
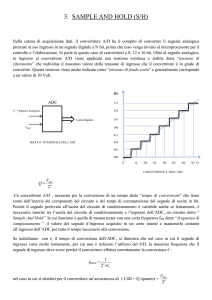
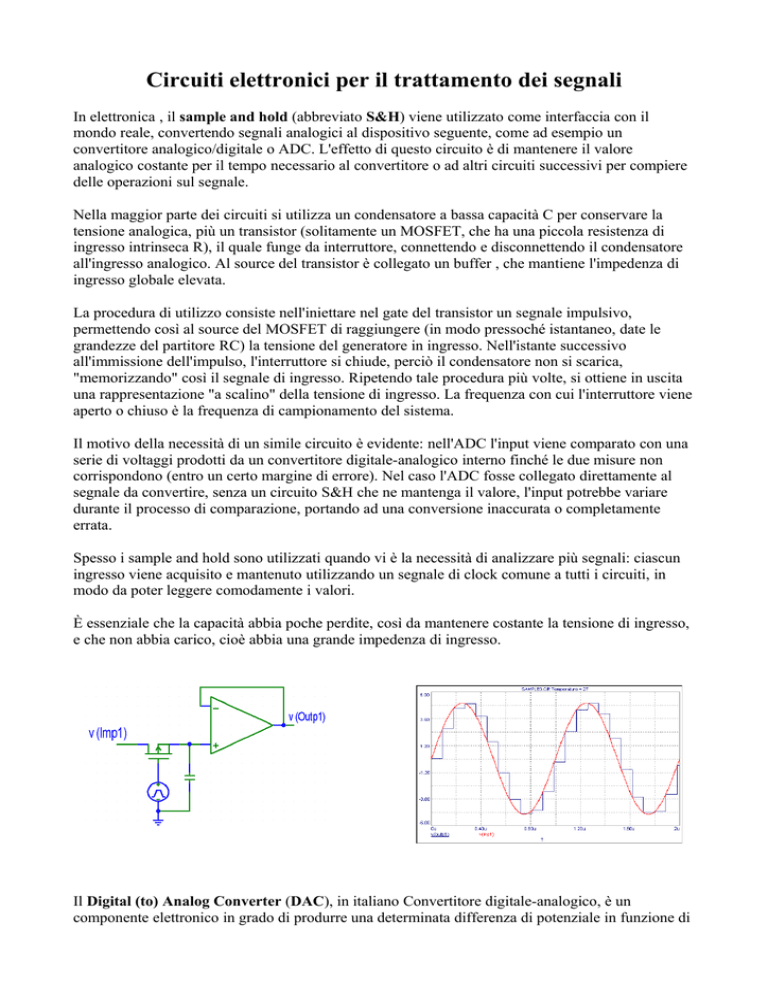
La procedura di utilizzo consiste nell'iniettare nel gate del transistor un segnale impulsivo,
permettendo così al source del MOSFET di raggiungere (in modo pressoché istantaneo, date le
grandezze del partitore RC) la tensione del generatore in ingresso. Nell'istante successivo
all'immissione dell'impulso, l'interruttore si chiude, perciò il condensatore non si scarica,
"memorizzando" così il segnale di ingresso. Ripetendo tale procedura più volte, si ottiene in uscita
una rappresentazione "a scalino" della tensione di ingresso. La frequenza con cui l'interruttore viene
aperto o chiuso è la frequenza di campionamento del sistema.
Il motivo della necessità di un simile circuito è evidente: nell'ADC l'input viene comparato con una
serie di voltaggi prodotti da un convertitore digitale-analogico interno finché le due misure non
corrispondono (entro un certo margine di errore). Nel caso l'ADC fosse collegato direttamente al
segnale da convertire, senza un circuito S&H che ne mantenga il valore, l'input potrebbe variare
durante il processo di comparazione, portando ad una conversione inaccurata o completamente
errata.
Spesso i sample and hold sono utilizzati quando vi è la necessità di analizzare più segnali: ciascun
ingresso viene acquisito e mantenuto utilizzando un segnale di clock comune a tutti i circuiti, in
modo da poter leggere comodamente i valori.
È essenziale che la capacità abbia poche perdite, così da mantenere costante la tensione di ingresso,
e che non abbia carico, cioè abbia una grande impedenza di ingresso.
Il Digital (to) Analog Converter (DAC), in italiano Convertitore digitale-analogico, è un
componente elettronico in grado di produrre una determinata differenza di potenziale in funzione di
un valore numerico che viene caricato; ad esempio, ad un valore pari ad 1 corrisponderà una
tensione di uscita di 0,1 V, ad un valore di 2 avremo 0,2 V e così via. La tabella di conversione dal
valore digitale a quello analogico prende il nome di LUT (Look-Up Table) e può avere
caratteristiche proporzionali (come nel precedente esempio), o può seguire un andamento del tutto
arbitrario, a seconda del suo impiego.
Una larga diffusione ad uso domestico dei DAC si ha nei riproduttori digitali di suoni, nel controllo
dell'apertura del diaframma nelle macchine fotografiche, nei controlli digitali (volume, luminosità)
dei televisori e in tutte quelle situazioni nelle quali un'informazione numerica deve controllare una
grandezza di tipo analogico.
Le caratteristiche del DAC hanno più o meno rilevanza a seconda dell'impiego; ad esempio la
risoluzione è estremamente importante per le misure di precisione e la riproduzione di brani
musicali ad alta fedeltà, e la qualità sarà tanto più alta, quanto maggiore sarà la grandezza massima
riproducibile sul suo ingresso digitale. Si va dagli 8 bit (256 livelli di tensione) dei DAC più
semplici (telecomandi ecc...), ai 12 bit per i controlli di precisione (strumenti di misura, multimetri,
oscilloscopi), ai 16 bit per i riproduttori musicali ad alta fedeltà (16 bit permettono di riprodurre una
dinamica di 96 dB),fino ad arrivare al DVD che, con i suoi 24 bit di risoluzione, consente una
dinamica teorica di ben 144 dB.
All'aumentare della risoluzione, però, corrisponde un maggior numero di elaborazioni per ottenere
la tensione d'uscita; in altre parole, più è elevata la risoluzione del DAC e più la sua elaborazione ne
risulterà rallentata. Pertanto, la scelta della risoluzione dovrà obbligatoriamente tenere conto della
velocità del dispositivo impiegato, rispetto all'utilizzo al quale è destinato.
Le possibili strutture circuitali sono:
•
DAC a resistenze di Emettitore potenza del 2
I convertitori DAC a commutazione di corrente hanno una coppia differenziale per pilotare le linee
di uscita (Io e -Io) e ricevono la corrente da commutare dal collettore di un transistor tipicamente
bipolare il cui Emettitore ha una singola resistenza verso l'alimentazione negativa La base di tutti i
transistor sono pilotate dal servosistema di riferimento La loro uscita è tipicamente una corrente e se
il riferimento è un segnale esterno, il DAC diventa DAC Moltiplicatore
•
DAC a rete R-2R
La singola resistenza di Emettitore dà problemi costruttivi a causa del grande rapporto tra la
resistenza dell'MSB e quella dell'LSB
Una tecnica in grado di rendere facile costruire reti con un'ottimo comportamento in un'ampia
variazione termica è la R-2R dove i valori della rete sono solo due, e quindi mettendo 2N+1
resistenze nel circuito avremo una rete ad N bit
L'uscita di questo convertitore è quasi sempre una corrente
•
DAC flash
Questo convertitore è un convertitore a resistenza d'emettitore singola od a rete R-2R ,il cui dato
d'ingresso passa attraverso un flip-flop D aggiunto per evitare il jitter e migliorare i percorsi dei
segnali all'interno del componente
•
DAC CMOS moltiplicante
Se le linee della rete R-2R sono commutate direttamente senza passare attraverso un transistor ed al
nodo principale viene fornito un segnale ,questo circuito moltiplica il dato d'ingresso D per la
tensione d'ingresso ottenendo Vu = D / 2N
L'uscita di questo convertitore è una tensione
•
DAC ad 1 bit o convertitore Sigma-Delta
Usando una tecnica di sovracampionamento si può commutare la tensione di pilotaggio di un
integratore la cui uscita sarà filtrata a frequenza molto inferiore
Questo convertitore è a basso costo e rende grandi risoluzioni senza necessità di circuiti precisi
,infatti la precisione avviene digitalmente all'interno della logica di pilotaggio e le sole parti precise
saranno la tensione di riferimento e la velocissima frequenza di clock
L'uscita di questo convertitore è una tensione
•
DAC a capacità commutate
Questo convertitore è spesso usato nei microcontrollori e la sua attività si svolge nello scambio di
carica tra un riferimento ( destinato a caricare un condensatore MOS ) ed un punto di misura
La tensione d'uscita è data dalla posizione dei commutatori CMOS
Il convertitore analogico-digitale, è un circuito elettronico in grado di convertire una grandezza
continua (ad es. una tensione) in una serie di valori discreti (vedi teoria sulla conversione analogicodigitale). Il convertitore digitale-analogico o DAC compie l'operazione inversa.
La risoluzione di un convertitore indica il numero di valori discreti che può produrre. È usualmente
espressa in bit. Per esempio, un ADC che codifica un ingresso analogico in 256 livelli discreti ha
una risoluzione di 8 bit, essendo 28 = 256. La risoluzione può anche essere definita elettricamente,
ed espressa in volt. La risoluzione in volt di un ADC è uguale alla minima differenza di potenziale
tra due segnali che vengono codificati con due livelli distinti adiacenti. Alcuni esempio possono
aiutare:
•
Esempio 1:
• Range compreso tra 0 e 10 volt
12
• Risoluzione dell'ADC di 12 bit: 2 = 4096 livelli di quantizzazione
•
•
La differenza di potenziale tra due livelli adiacenti è 10 V / 4096 = 0,00244 V = 2,44
mV
Esempio 2:
• Range compreso tra -10 e 10 volt
14
• Risoluzione dell'ADC di 14 bit: 2 = 16384 livelli di quantizzazione
• La differenza di potenziale tra due livelli adiacenti è 20 V / 16384 = 0,00122 V =
1,22 mV
Nella pratica, la risoluzione di un convertitore è limitata dal rapporto segnale/rumore (S/N ratio) del
segnale in questione. Se è presente troppo rumore all'ingresso analogico, sarà impossibile convertire
con accuratezza oltre un certo numero di bit di risoluzione. Anche se l'ADC produrrà un valore,
questo non sarà accurato essendo i bit meno significativi funzione del rumore e non del segnale. Il
rapporto S/N dovrebbe essere di circa 6 dB per bit.
La maggior parte degli ADC sono lineari, il che significa che sono progettati per produrre in uscita
un valore che è funzione lineare del segnale di ingresso. Un altro tipo comune di ADC è quello
logaritmico, che è usato in sistemi di comunicazioni vocali per aumentare l'entropia del segnale
digitalizzato.
L'istogramma di un segnale vocale ha la forma di due curve esponenziali inverse, e l'ADC non
lineare cerca di approssimare questo con una funzione di densità di probabilità quadrata come a-law
o μ-law, funzioni logaritmiche. Il segnale distorto ha un range dinamico inferiore, e la sua
quantizzazione aggiunge meno rumore al segnale originale rispetto a quanto farebbe un
quantizzatore lineare con la stessa risoluzione in bit.
L'accuratezza dipende dall'errore della conversione. Questo errore è formato da due componenti: un
errore di quantizzazione e un errore di non-linearità (o infedeltà alla curva desiderata nel caso di
ADC volutamente non-lineari). Questi errori sono misurati con un'unità chiamata LSB (least
significant bit = bit meno significativo) ed indica fino a che punto i bit rappresentano segnale e
quanti siano solo rumore. In un ADC a 8 bit, un errore di 1 LSB è pari ad un errore di 1/256 ossia
circa del 0,4%; è un modo per dire che l'ultimo bit è causale. In un ADC a 16 bit con un errore di 4
LSB significa che l'errore risulterà pari a 4/(216) ossia 0,006%.
L'errore di quantizzazione è dovuto alla risoluzione finita dell'ADC ed è una imperfezione
intrinseca di tutti i tipi di ADC. La grandezza dell'errore di quantizzazione su un campione è
compresa tra zero e un LSB.
Tutti gli ADC soffrono di errori di non-linearità causati da imperfezioni fisiche, facendo deviare la
loro l'uscita da una funzione lineare (o da un'altra funzione, in caso di ADC volutamente nonlineari). Questi errori possono a volte essere attenuati con una calibrazione.
Parametri importanti per la linearità sono non-linearità integrale (INL) e non linearità differenziale
(DNL).
Il segnale analogico è tempo-continuo ed è necessario convertirlo in un flusso di valori discreti. È
quindi necessario definire una frequenza alla quale campionare i valori discreti del segnale
analogico. Questa frequenza è chiamata sampling rate (frequenza di campionamento, in italiano) del
convertitore.
L'idea chiave è che un segnale di banda limitata che varia con continuità può essere campionato e
poi riprodotto esattamente dai valori tempo discreti con un algoritmo di interpolazione se la
frequenza di campionamento è almeno pari al doppio della banda del segnale (legge di Shannon).
L'accuratezza tuttavia è limitata dall'errore di quantizzazione.
Poiché nella pratica un ADC non può effettuare una conversione istantanea, il valore d'ingresso
deve necessariamente rimanere costante durante il tempo che il convertitore esegue la conversione
(chiamato tempo di conversione o conversion time). Un circuito d'ingresso chiamato sample/hold
svolge questo compito - spesso si usa un condensatore per immagazzinare la tensione del segnale in
input e un interruttore elettronico per disconnettere il condensatore dall'ingresso. Molti ADC
realizzati su circuiti integrati realizzano il sottosistema di sample/hold internamente.
Tutti gli ADC lavorano campionando il proprio input ad intervalli discreti di tempo. L'output di
conseguenza è un'immagine incompleta dell'input e non c'è modo di sapere, guardando soltanto
l'output, che valori abbia assunto l'input tra due istanti di campionamento adiacenti. Se è noto che
l'ingresso varia lentamente confrontato con la frequenza di campionamento, allora si può presumere
che esso sia sempre contenuto tra i due estremi in quell'intervallo. Il risultato diretto che si osserva
riproducendo un segnale campionato ad una frequenza inferiore della sua banda è che le
componenti del segnale a frequenze superiori verranno riprodotti a frequenza diverse, inferiori alla
frequenza di campionamento. Ad esempio, campionando a 1.5 kHz un onda sinusoidale a 2 kHz
verrà trasformata in una onda a 500 Hz (ed in opposizione di fase). Il problema dell'aliasing può
essere osservato anche visivamente, basta far caso che in televisione o al cinema (dove l'immagine è
campionata a 25 Hz), oggetti in rotazione a frequenza superiori, come pale di elicottero o ruote di
automobili, spesso ci appaiano girare lentamente, o addirittura al contrario, rispetto a quanto ci si
aspetterebbe.
Per eliminare l'aliasing, l'ingresso di un ADC deve essere filtrato (low-pass) per rimuovere le
frequenze superiori a quelle di campionamento. Questo filtro è chiamato anti-aliasing ed è
essenziale in un sistema ADC.
Il dithering consiste nell'introdurre artificialmente del rumore nel segnale di ingresso al fine di
migliorare la qualità di conversione superando la limitazione di una risoluzione finita. Anche se può
sembrare assurdo che del rumore possa migliorare la qualità si può mostrare come questo sia vero
con un semplice esempio numerico. Supponiamo che il segnale di ingresso sia sempre pari e
costante al valore di 0,34 Volt e che il nostro convertitore abbia una risoluzione di 0,1 volt. In
assenza di rumore il segnale sarà campionato e approssimato come una sequenza di valori pari a 0,3
V, il livello più vicino del quantizzatore. Se invece sommiamo del rumore bianco, cioè un segnale
con valore medio nullo, con una varianza pari a 0,1 V (pari alla risoluzione del convertitore, 1LSB)
avremo che il segnale oscillerà ora tra 0,24 V e 0,44 V con il risultato che i campioni avranno i
valori di 0,2, 0,3 o 0,4 Volt. Per le proprietà statistiche del rumore, il valor medio dei campioni,
invece di 0,3 volt, sarà di 0,34 V: in pratica il rumore ha annullato l'errore medio.
Osservando la figura, è chiaro come l'errore in assenza di dither si sommi nel tempo essendo le due
linee spesse parallele mentre la linea sottile, oscillando attorno al valore esatto, lo approssima in
valor medio sempre di più al passare del tempo.
In elettronica ci sono cinque modi comuni di implementare un ADC:
•
•
Un ADC a conversione diretta o flash ADC ha un comparatore per ognuno dei livelli di
voltaggio riconosciuti dal quantizzatore. Un ADC flash ad 8-bit avrà 2^8-1 (=256-1)
comparatori. Il segnale di ingresso arriva a tutti i comparatori, ma solo uno di essi attiverà la
propria uscita, quello del livello corrispondente. I convertitori flash sono i più veloci in
assoluto e sono usati per campionare segnali in alta frequenza, fino a diversi GHz. Poiché il
numero di comparatori necessari cresce esponenzialmente con il numero dei bit richiesti, i
convertitori flash raramente hanno più di 8 bit di risoluzione.
Un ADC ad approssimazioni successive usa un comparatore e un DAC, ad ogni passaggio
l'ADC prova a impostare un bit, partendo dal MSB e usando il DAC confronta il segnale
campionato con il segnale di ingresso in feedback. Questo convertitore individua un bit ad
ogni iterazione in una sorta di ricerca binaria e la risoluzione è limitata solo dalle esigenze di
sample-rate e dal rumore in ingresso.
•
Un ADC a codifica-delta ha un contatore up-down collegato ad un DAC. Un comparatore
confronta il segnale di uscita del DAC con il segnale di ingresso e interrompe il conteggio
quando i valori sono abbastanza vicini tra loro. Quando questo succede il contatore contiene
il livello quantizzato del segnale. Questi convertitori sono usati spesso per leggere grandezze
fisiche che non variano con elevata velocità ma che devono essere lette con molta
precisione.
•
Un ADC a doppia rampa (o ad integrazione) produce un segnale a dente di sega che sale,
per poi cadere velocemente a zero. Il segnale di ingresso viene integrato facendo salire la
rampa mentre un contatore segna il tempo. Quando la rampa raggiunge un livello noto il
conteggio termina e indica il valore quantizzato del segnale. Questo tipo di ADC è sensibile
alla temperatura poiché può alterare il clock usato per segnare il tempo o alterare il voltaggio
di riferimento per la rampa e deve essere ricalibrato spesso.
•
Un ADC a pipeline (noto anche come subranging quantizer) è simile al ADC ad
approssimazioni successive ma invece di individuare un bit alla volta individua un blocco di
bit; in un primo passo avviene una conversione grezza del segnale che viene poi riconvertito
da un DAC; quindi si quantizza la differenza tra il segnale originario e quello campionato,
eventualmente si può procedere a quantizzazioni sempre più fini con passi successivi. Se ad
esempio supponiamo di avere un quantizzatore a 4-bit che operi con un range di [0÷2,56 V]
(quindi con una risoluzione di 0,16 V) e un altro quantizzatore a 4-bit che operi però tra [0 V
÷ 0,16 V] con una risoluzione di 0,01 V. Dopo aver quantizzato il segnale di ingresso con il
primo quantizzatore la differenza tra il segnale quantizzato e quello di ingresso sarà al
massimo quello della risoluzione, e può essere letto dal secondo quantizzatore. Se il segnale
di ingresso era pari a 2.50 V, il primo campionatore indentificherà il livello 15 (1111 in
binario), che corrisponde ad un valore di 2,40 V, la differenza di 1,0 V viene quantizzata dal
secondo con il livello 10 (1010 in binario); unendo i codici si ottiene 1111 1010 ossia un
valore a 8 bit.