Calcolo della resistenza di linearizzazione Analizziamo il

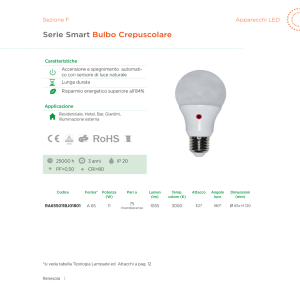
Linearizzazione della caratteristica di un sensore
Calcolo della resistenza di linearizzazione
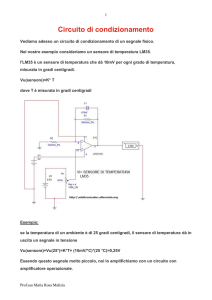
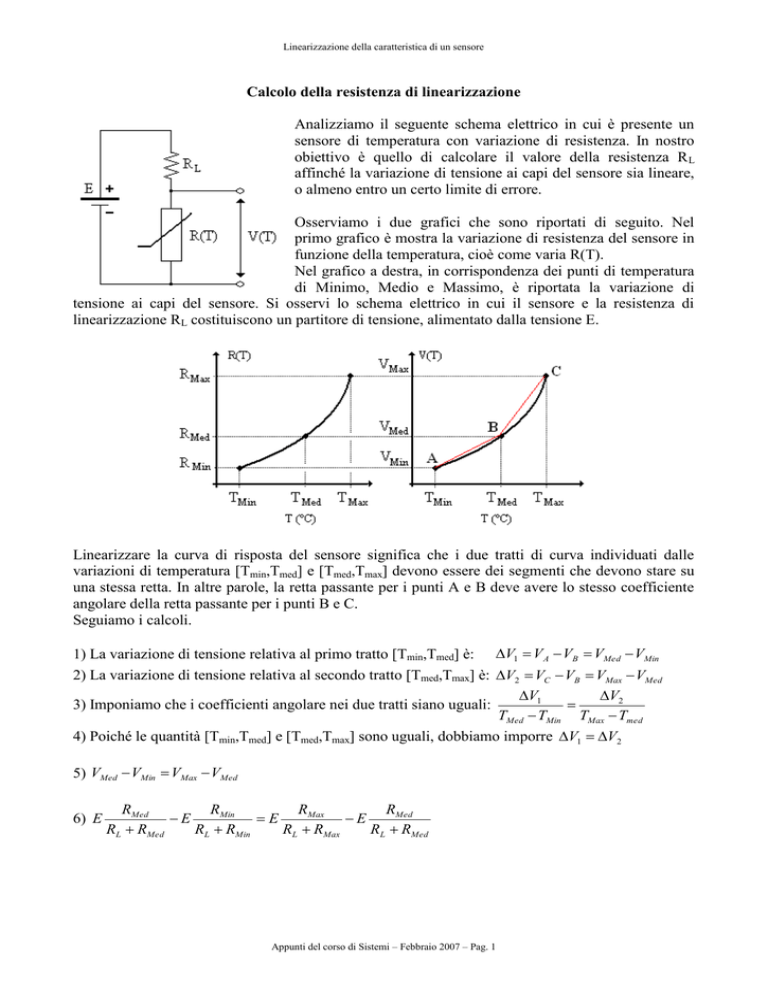
Analizziamo il seguente schema elettrico in cui è presente un
sensore di temperatura con variazione di resistenza. In nostro
obiettivo è quello di calcolare il valore della resistenza R L
affinché la variazione di tensione ai capi del sensore sia lineare,
o almeno entro un certo limite di errore.
Osserviamo i due grafici che sono riportati di seguito. Nel
primo grafico è mostra la variazione di resistenza del sensore in
funzione della temperatura, cioè come varia R(T).
Nel grafico a destra, in corrispondenza dei punti di temperatura
di Minimo, Medio e Massimo, è riportata la variazione di
tensione ai capi del sensore. Si osservi lo schema elettrico in cui il sensore e la resistenza di
linearizzazione RL costituiscono un partitore di tensione, alimentato dalla tensione E.
Linearizzare la curva di risposta del sensore significa che i due tratti di curva individuati dalle
variazioni di temperatura [Tmin,Tmed] e [Tmed,Tmax] devono essere dei segmenti che devono stare su
una stessa retta. In altre parole, la retta passante per i punti A e B deve avere lo stesso coefficiente
angolare della retta passante per i punti B e C.
Seguiamo i calcoli.
1) La variazione di tensione relativa al primo tratto [Tmin,Tmed] è: V1  V A  VB  VMed  VMin
2) La variazione di tensione relativa al secondo tratto [Tmed,Tmax] è: V2  VC  VB  VMax  VMed
V1
V2

3) Imponiamo che i coefficienti angolare nei due tratti siano uguali:
TMed  TMin TMax  Tmed
4) Poiché le quantità [Tmin,Tmed] e [Tmed,Tmax] sono uguali, dobbiamo imporre V1  V2
5) VMed  VMin  VMax  VMed
6) E
RMed
RMin
RMax
RMed
E
E
E
RL  RMed
RL  RMin
RL  RMax
RL  RMed
Appunti del corso di Sistemi – Febbraio 2007 – Pag. 1
Linearizzazione della caratteristica di un sensore
7) Mettendo in evidenza Rmed al denominatore della prima frazione e semplificando, Rmin nella
seconda frazione, e così via per le altre frazioni, si ottiene:
1
1
1
1



R
R
R
R
1 L
1 L
1 L
1 L
RMed
RMin
RMax
RMed
Per facilitare lo sviluppo dei calcoli, poniamo:
X Min 
RL
R
R
; X Med  L ; X Max  L
RMin
RMed
RMax
8) Dalla 7) se ottiene: ( X Min  X Med )(1  X Max )  ( X Med  X Max )(1  X Min )
9)
1
1
1
1
1
1
1
1
1
(
2

)
(

)2
RL RMin
RMed RMax
RMed RMin RMax
RMin RMax
10) Dopo qualche semplice calcolo e qualche semplificazione si ottiene la resistenza di
linearizzazione, ossia:
RL 
RMax * ( RMed  RMin )  RMin * ( RMax  RMed )
( RMax  RMed )  ( RMed  RMin )
A titolo di esempio consideriamo il
sensore di temperatura a variazione
di resistenza della Philips KTY.
Dalla figura che segue si vede
l’andamento non lineare del sensore,
la curva di R(T) tra –55 °C e 150 °C
non è una retta. A lato del grafico è
riportato una tabella dei valori di
R(T) nel range di temperatura tra –55
°C e 150 °C. All’interno di questo
range di variazione si ha:
RMin R(50C )  515
RMed R(50C )  1209
RMax  R(150C )  2211
Calcoliamo la pendenza della curva
nel primo tratto, cioè:
m1 
R1 RMed  RMin

 6.94
T TMed  TMin
m2 
R2 RMax  RMed

 9.21
T
TMax  TMed
Appunti del corso di Sistemi – Febbraio 2007 – Pag. 2
Linearizzazione della caratteristica di un sensore
Si vede che il secondo tratto si discosta dal primo per il 32%, volendo indicare una non linearità
della curva. Considerando il circuito elettrico riportato all’inizio, calcoliamo i valori di tensione ai
capi del sensore nell’ipotesi che il generatore sia E=10 Volt. Si ha:
VMin E
RMin
 1.34
RL  RMin
VMed  E
RMed
 2.68
RL  RMed
VMax  E
RMax
 4.00
RL  RMax
Calcoliamo i coefficienti angolari dei tratti VMin-VMed e del tratto VMed-VMax. Si ha:
m1 
V1 VMed  VMin

 1.33
T TMed  TMin
m2 
V2 VMax  VMed

 1.33
T TMax  TMed
Da cui si vede che i tre punti Vmin , Vmed e VMax si trovano sulla stessa retta. Ciò sta a significare che
la curva del sensore è stata linearizzata e fornisce una risposta lineare.
Allo stesso modo si può pensare di mettere la resistenza RL in parallelo al sensore, come nello
schema che segue. Anche in questo caso avremo una linearizzazione della caratteristica del sensore.
Si provi a calcolare il parallelo di R(T) e di RL per le temperature Tmin , Tmed , Tmax e si verifichi che
i tre valori sono proporzionali, ossia stanno sulla stessa retta.
Appunti del corso di Sistemi – Febbraio 2007 – Pag. 3