NUMERI PRIMI INDIVIDUATI COL CRIVELLO DI ERATOSTENE E CON DIVISIONI
di Luciano Porta
Definiamo numero primo e numero composto.
numero primo: numero maggiore di 1 divisibile solo per 1 e per se stesso;
numero composto: numero maggiore di 1 divisibile per 1, per se stesso e almeno un altro divisore.
Iniziamo preparando una tabella con alcuni numeri interi di cui indichiamo i divisori e che
conseguentemente classifichiamo come primi o composti.
NUMERO
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16 …
DIVISORI
1-2
1-3
1–2-4
1-5
1–2–3-6
1-7
1–2–4-8
1–3 -9
1 – 2 – 5 - 10
1 - 11
1 – 2 – 3 – 4 – 6 - 12
1 - 13
1 – 2 – 7 - 14
1 – 3 – 5 - 15
1 – 2 – 4 – 8 - 16
PRIMO-COMPOSTO
PRIMO
PRIMO
COMPOSTO
PRIMO
COMPOSTO
PRIMO
COMPOSTO
COMPOSTO
COMPOSTO
PRIMO
COMPOSTO
PRIMO
COMPOSTO
COMPOSTO
COMPOSTO
Osserviamo che:
- i numeri pari, ad eccezione del
2, sono composti;
- tra i numeri dispari solo alcuni
sono primi;
- i numeri composti possono
essere scritti come prodotto di
fattori primi es. 6=2*3;
8=2*2*2; 9=3*3; 15=3*5 …
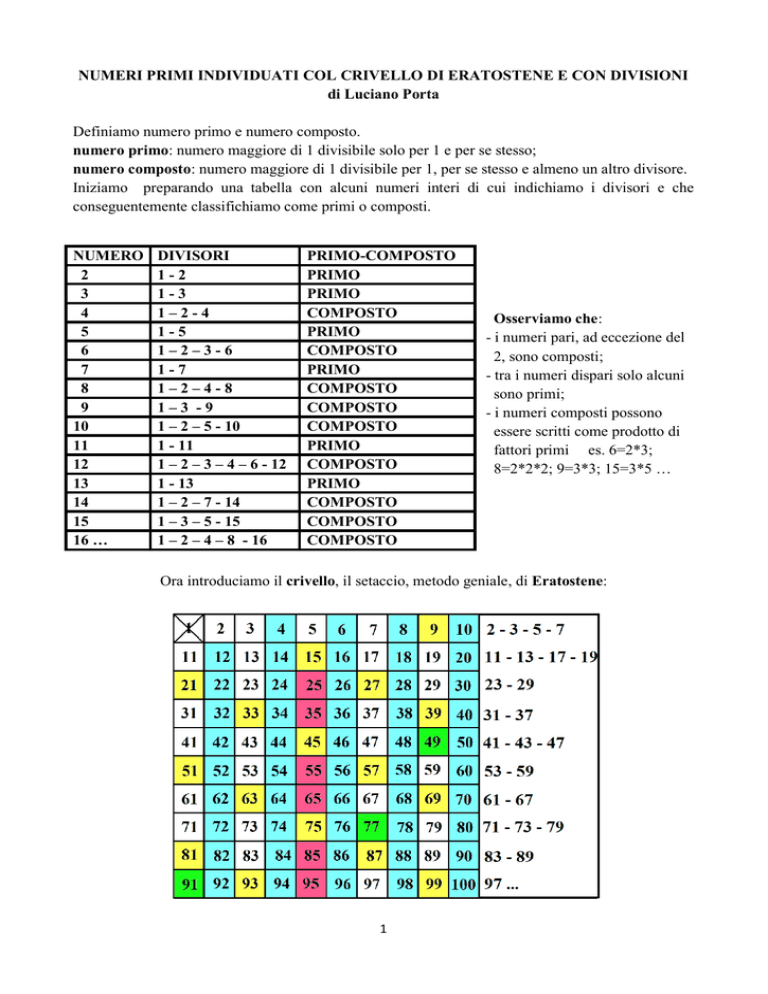
Ora introduciamo il crivello, il setaccio, metodo geniale, di Eratostene:
1
In una tabella si scrivono i numeri naturali in successione fino al numero voluto.
Eliminiamo subito il numero 1 che non è né primo, né composto.
Eliminiamo i multipli di 2, eccetto il 2 (nel disegno questi numeri sono in caselle azzurre).
Eliminiamo i multipli (ancora presenti) di 3, eccetto il 3 (caselle gialle).
Eliminiamo i multipli (ancora presenti) di 5, eccetto il 5 (caselle rosse).
Eliminiamo i multipli (ancora presenti) di 7, eccetto il 7 (caselle verdi) e così via con i multipli dei
numeri primi rimasti.
Rimangono nelle caselle bianche i numeri primi in successione, trascritti accanto alla tabella.
E’ opportuno memorizzarli almeno fino al 97.
Se invece, dato un numero, dobbiamo stabilire se è primo o composto, possiamo ricorrere al
metodo delle divisioni ordinate dei numeri primi.
Verifichiamo se è divisibile per un elemento della successione dei numeri primi : 2, 3, 5. 7, 11,
13, 17, 19, 23, 29, 31, 37 … fino a al numero dato.
Se nessuno dei numeri provati (eccetto il numero stesso) è divisore affermiamo che il numero dato
è primo.
Es. dato il numero 23, il procedimento è il seguente:
23:2 NO;23:3 NO;23:5 NO;23:7 NO;23:11 NO;23:13 NO;23:17 NO;23:19 NO;23:23 SI e quindi il
numero 23 è primo.
Questo metodo, didatticamente valido, non è molto adatto per numeri grandi.
Può tuttavia essere reso molto più sintetico e rapido.
Innanzi tutto è superfluo applicarlo sui numeri pari che, ad eccezione del 2, sono composti.
Dopo alcune riflessioni impareremo a provare un numero molto minore di possibili divisori per
avere la certezza che un numero è primo
Numeri composti:
DIVIDENDO = 12
DIVISORI
QUOZIENTI
1
12
2
6
3
4
4
3
6
2
12
1
DIVIDENDO = 15
DIVIDENDO = 16
DIVISORI
QUOZIENTI
1
16
2
8
4
4
8
2
16
1
DIVISORI
QUOZIENTI
1
15
3
5
5
3
15
1
DIVIDENDO = 25
DIVISORI
QUOZIENTI
1
25
5
5
25
1
2
Numeri primi:
DIVIDENDO = 19
DIVISORI
QUOZIENTI
1
19
19
1
DIVIDENDO = 41
DIVISORI
QUOZIENTI
1
41
41
1
Osserviamo (vedi caselle azzurre e caselle bianche in diagonale) che ad un certo punto, sia
per i numeri primi, sia per i numeri composti, al massimo eguagliata la radice quadrata del
dividendo, avviene lo scambio tra divisori e quozienti.
Esponiamo allora il metodo sintetico e rapido:
1) se il numero è pari ed è diverso da 2 è composto (es. 3134; 1792; 1350; 3760);
2) se il numero è dispari verifichiamo se è divisibile per i numeri primi considerati in modo
ordinato escludendo il 2 ( quindi per 3 – 5 – 7 – 11 – 13 – 17 – 19 – 23 – 29 … ).
Se uno di questi primi è divisore il numero dato è composto.
Ci fermiamo, avendo la certezza che il numero dato è primo se il numero primo successivo a
quello provato inutilmente come divisore moltiplicato per se stesso supera il numero dato.
Es. 323
323:3 NO 323:5 NO 323:7 NO 323:11 NO 323:13 NO 323:17 SI COMPOSTO
(ho provato come divisore anche il 17 perché 13*13=169 < di 323; se neppure il 17 fosse stato
divisore mi sarei fermato certo che 323 era primo poiché 19*19=361 > 323).
Es. 431
431:3 NO 431:5 NO 431:7 NO 431:11 NO 431:13 NO 431:17 NO 431:19 NO
(non provo 431:23 poiché 23*23=529 > 431) PRIMO.
Praticamente:
3578 COMPOSTO (è pari);
1369 COMPOSTO perché 3 5 7 11 13 17 19 23 29 31 37 SI (non mi sono fermato al 31
perché 31*31=961 < 1369 e 37*37=1369; ricordo che il numero al quadrato non deve
superare il dividendo);
1511 PRIMO perché 3 5 7 11 13 17 19 23 29 31 37 (ho provato inutilmente come ultimo
divisore il 37 poiché 37*37=1369 < 1511 e 41*41=1681 > 1511).
www.webalice.it/lucianoporta i Pitagorici DIDATTICA E DIVULGAZIONE DELLA MATEMATICA E DELLE SCIENZE LEZIONI TRE
3












