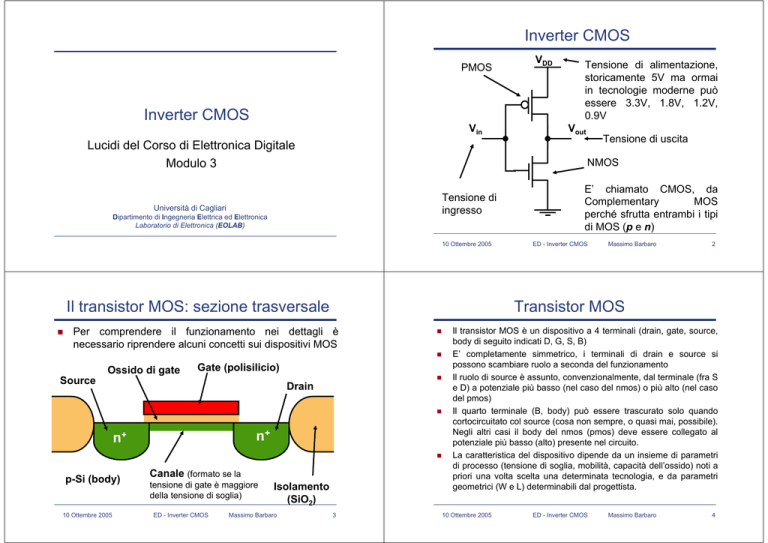
Inverter CMOS
PMOS
Inverter CMOS
Vin
Lucidi del Corso di Elettronica Digitale
Modulo 3
Tensione di
ingresso
Università di Cagliari
10 Ottembre 2005
Il transistor MOS: sezione trasversale
Source
Gate (polisilicio)
Drain
n+
n+
p-Si (body)
10 Ottembre 2005
Canale (formato se la
tensione di gate è maggiore
della tensione di soglia)
ED - Inverter CMOS
Isolamento
(SiO2)
Massimo Barbaro
Vout
Tensione di uscita
E’ chiamato CMOS, da
Complementary
MOS
perché sfrutta entrambi i tipi
di MOS (p e n)
ED - Inverter CMOS
Massimo Barbaro
2
Transistor MOS
Per comprendere il funzionamento nei dettagli è
necessario riprendere alcuni concetti sui dispositivi MOS
Ossido di gate
Tensione di alimentazione,
storicamente 5V ma ormai
in tecnologie moderne può
essere 3.3V, 1.8V, 1.2V,
0.9V
NMOS
Dipartimento di Ingegneria Elettrica ed Elettronica
Laboratorio di Elettronica (EOLAB)
VDD
3
Il transistor MOS è un dispositivo a 4 terminali (drain, gate, source,
body di seguito indicati D, G, S, B)
E’ completamente simmetrico, i terminali di drain e source si
possono scambiare ruolo a seconda del funzionamento
Il ruolo di source è assunto, convenzionalmente, dal terminale (fra S
e D) a potenziale più basso (nel caso del nmos) o più alto (nel caso
del pmos)
Il quarto terminale (B, body) può essere trascurato solo quando
cortocircuitato col source (cosa non sempre, o quasi mai, possibile).
Negli altri casi il body del nmos (pmos) deve essere collegato al
potenziale più basso (alto) presente nel circuito.
La caratteristica del dispositivo dipende da un insieme di parametri
di processo (tensione di soglia, mobilità, capacità dell’ossido) noti a
priori una volta scelta una determinata tecnologia, e da parametri
geometrici (W e L) determinabili dal progettista.
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
4
MOS: equazione caratteristica classica
(V − V
V
= k (V − V )V −
2
W
I =µC
L
D
n
OX
GS
GS
Tn
DS
k
I = (V − V
2
GS
k =µC
n
n
10 Ottembre 2005
D
2
Tn
ID =
DS
W
L
ED - Inverter CMOS
V
I = k (V − V )V −
2
DS
D
Triodo
5
GS
Tn
10 Ottembre 2005
Saturazione
VDS
ED - Inverter CMOS
Massimo Barbaro
ID
La corrente è positiva
quando scorre dal
source al drain
Le curve crescono
all’aumentare di VSG (al
diminuire di VG)
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
6
VSG=5
VGS=4
VSG=4
VGS=3
VSG=3
L’asse delle ascisse è VSD
(quindi la corrente aumenta al
diminuire di VD)
VGS=2
VGS=1
VGS=0
DS
PMOS: Caratteristica al variare di VSG
VGS=5
Le curve non sono orizzontali per
l’effetto di modulazione della
lunghezza di canale
n
VGS-VTn
Massimo Barbaro
Saturazione
kn
(VGS − VTn )2
2
2
Rapporto di forma:
unico parametro
modificabile dal progettista
2
VDS=VGS-VTn
Triodo
GS
ID
NMOS: Caratteristica al variare di VGS
ID
n
DS
)
Tn
OX
2
Equazione in regione
di saturazione
n
D
I = k (V − V )V
)V − V =
2
Equazione in
regione lineare
DS
Tn
DS
n
MOS: Regioni di funzionamento
VSG=2
VSG=1
VSG=0
VDS
7
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
VSD
8
MOS come interruttore
Interruttore NMOS
In elettronica digitale il transistor MOS viene
fondamentalmente usato come interruttore,
quindi in prima approssimazione possiamo dire
che:
NMOS: è spento per tensioni gate-source minori
della tensione di soglia (VGS<VTn) ed è acceso ed
equivalente ad una resistenza (piccola) RON per
tensioni gate-source maggiori della tensione di
soglia.
PMOS: è spento per tensioni source-gate minori
della tensione di soglia in valore assoluto
(VSG<|VTp|) ed è acceso ed equivalente ad una
resistenza (piccola) RON per tensioni source-gate
maggiori della tensione di soglia.
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
9
Interruttore PMOS
VSG>|VTp|
S
E’ sicuramente
acceso se
VG=VDD
G
S
E’ sicuramente
spento se VG=0
VGS<VTn
Il terminale di source è
(tipicamente) quello in basso ed
è collegato alla massa
10 Ottembre 2005
ED - Inverter CMOS
ED - Inverter CMOS
10
Vin=0
Vout
Vin
Il terminale di source è
(tipicamente) quello in alto ed è
collegato all’alimentazione (VDD)
Massimo Barbaro
Nelle resistenze non scorre VDD
corrente quindi ∆V=R•I=0
RON
E’ sicuramente
acceso se VG=0
VSG<|VTp|
Circuito
aperto
Inverter: funzionamento di massima
G
10 Ottembre 2005
RON
VGS>VTn
E’ sicuramente
spento se
VG=VDD
Vout=0
Vin=VDD
Circuito
aperto
Massimo Barbaro
Vout=VDD
11
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
12
Inverter: funzionamento di massima
Vin=0
Ma
perché
possiamo
affermare che la corrente è
esattamente
uguale
a
zero?
Inverter: VTC
VDD
La corrente non può
scorrere
verso
massa
perché
lo
NMOS
è
interdetto.
Vout
Vout2
Non può scorrere verso il
carico perché ci sono i gate
di un PMOS ed un NMOS
che sono circuiti aperti.
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
13
Se il comportamento di massima è giustamente quello di
un inverter come è la VTC?
E’ necessario costruirla per punti conoscendo le curve
caratteristiche dei due MOS al variare della tensione
gate-source.
Procedimento: si impone che le correnti del pmos e del
nmos siano uguali (lo sono perché non ci sono altri
possibili percorsi per la corrente). Graficamente questo
significa disegnare le caratteristiche dei due mos sullo
stesso grafico e trovare i punti di intersezione
Nel caso del NMOS: VGS=Vin , VDS=Vout
Nel caso del PMOS: VSG=VDD-Vin , VSD=VDD-Vout
10 Ottembre 2005
ED - Inverter CMOS
Inverter: VTC
Massimo Barbaro
14
Inverter: VTC
IDn , IDp
VDD
PMOS
NMOS
VSGp=VDD -Vin
IDp
Vin
VSDp=VDD -Vout
Vout
IDn=IDp
IDn
VGSn =Vin
VDSn=Vout
Perché la corrente
non può andare
da nessun’altra
parte
Vin=3
Vin=2
Vin=4
Vin=1
Vin=5
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
15
10 Ottembre 2005
Vin=0
ED - Inverter CMOS
Massimo Barbaro
Vout
16
Inverter: VTC
Inverter: VTC
IDn , IDp
Vin=5
Vin=0
Vin=1
Vin=3
Vin=4
DD
(c)
Vin=3
Vin=0 Vin=1
Vin=4
ED - Inverter CMOS
nmos saturazione
nmos off
Vin=2
Vin=2
10 Ottembre 2005
La VTC è quella desiderata, ossia una VTC che gode
della proprietà rigenerativa
pmos triodo
Vout (a)
(b)
V
pmos saturazione
(d)
|VTp|
Vin=5
Massimo Barbaro
0
Vout
17
10 Ottembre 2005
VTn
ED - Inverter CMOS
nmos triodo
pmos off
(e)
Vin
Massimo Barbaro
Inverter VTC
La caratteristica è divisa in 5 zone:
Inverter CMOS
Calcolo dei parametri statici
Infatti lo NMOS è:
Pmos in triodo, nmos spento (a)
Pmos in triodo, nmos in saturazione (b)
Pmos in saturazione, nmos in saturazione (c)
Pmos in saturazione, nmos in triodo (d)
Pmos off, nmos in triodo (e)
Off se Vin<VTn
In triodo se Vout<Vin-VTn, in saturazione altrimenti
Infatti il PMOS è:
Off se Vin>VDD-|VTp|
In triodo se Vout>Vin+|VTp|, in saturazione altrimenti
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
19
Università di Cagliari
Dipartimento di Ingegneria Elettrica ed Elettronica
Laboratorio di Elettronica (EOLAB)
18
Parametri statici
Una volta ottenuta la VTC dell’inverter si
possono
ricavare
i
parametri
statici.
Banalmente:
Inverter: calcolo di VM
VOH = VDD
VOL = 0
Per ricavare VIL, VIH e VM bisogna utilizzare le
equazioni dei MOS
La soglia logica si trova imponendo che le due
correnti siano uguali e Vout=Vin . Tale condizione
si verificherà sicuramente nella zona (c) dove
entrambi i MOS sono in saturazione
VGS=Vin =VM
I Dn =
k
kn
(VM − VTn )2 = p (VDD − VM − | VTp |)2 = I Dp
2
2
VM =
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
21
r (VDD − | VTp |) + VTn
1+ r
10 Ottembre 2005
Soglia logica: considerazioni
kn=kp
µnCOX(W/L)n=µpCOX(W/L)p
ED - Inverter CMOS
Massimo Barbaro
Poiché, generalmente, la mobilità delle lacune è
inferiore a quella degli elettroni (in genere 1/3)
(W/L)p = (µn / µp) (W/L)n
10 Ottembre 2005
ED - Inverter CMOS
con
Massimo Barbaro
r=
kp
kn
22
Margini di rumore
La soglia logica è funzione del rapporto fra i fattori di
forma del pmos e del nmos
La condizione ideale (che rende la caratteristica
simmetrica e massimizza i margini di rumore) è quella in
cui VM=VDD/2
Visto che, nella totalità dei moderni processi CMOS
risulta VTn=|VTp|, tale condizione si ottiene per
VSG= VDD-Vin= VDD -VM
23
Per calcolare i margini di rumore è necessario
trovare VIL e VIH. Questo calcolo è agevole solo
nell’ipotesi, già fatta per ottimizzare la soglia
logica, di avere kn=kp
Per trovare VIH si ipotizza (come si deduce dalla
VTC) che tale punto debba trovarsi nella zona
(d) con nmos in triodo e pmos in saturazione
Si uguagliano le correnti del pmos e del nmos, si
deriva membro a membro rispetto a Vin e si
impone che la derivata dell’uscita sia –1 in
corrispondenza di VIH
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
24
Calcolo di VIH
k n (VIH − VTn )Vout −
NMH e NML
k
kn
Vout = p (VDD − VIH − | VTp |)
2
2
2
2
Nello stesso modo si ottiene VIL
1 3V
VIL = DD + VTn
4 2
Se kn=kp, VTn=|VTp|, derivando membro a membro rispetto a
Vin, ed imponendo che la derivata dell’uscita sia -1
VIH = Vout +
VDD
2
I margini di rumore risultano (sono uguali per la simmetria):
Inserendo questo risultato nell’equazione iniziale
3VDD VTn
NM H = NM L =
+
8
4
1 5V
VIH = DD − VTn
4 2
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
25
10 Ottembre 2005
Dimensionamento: considerazioni
ED - Inverter CMOS
Massimo Barbaro
Massimo Barbaro
26
Dimensionamento
Si è visto che la condizione kn=kp rende la
caratteristica simmetrica, posiziona la soglia
logica al centro del range di tensioni e
massimizza, contemporaneamente, i due
margini di rumore
Cosa succede se la condizione non è verificata?
Qualitativamente si può pensare in questo
modo: quando kn>kp lo NMOS è più conduttivo
(assorbe più corrente) quindi è più difficile
spegnerlo per portare l’uscita a 0 quindi la soglia
logica si sposta verso il basso. L’opposto
avviene se kn<kp
10 Ottembre 2005
ED - Inverter CMOS
27
Poiché l’obiettivo finale è sempre quello di avere i
dispositivi più piccoli possibili (anche perché sono più
veloci) per ottenere kn=kp si agisce sulle larghezze (W)
dei due MOS imponendo per ciascuno la lunghezza
minima ottenibile per una data tecnologia
Sarà quindi
Ln=Lp=Lmin
Wp= (µn / µp) Wn
Nello schematico di un circuito digitale, dunque, affianco
ad un transistor si mette un numero che rappresenta la
sua W (espressa in micron) dando per scontato che la L
sia la minima possibile
In tecnologie moderne la lunghezza di canale arriva a
Lmin= 0.13µ (Pentium 4). La stessa Intel prevede di
arrivare a Lmin= 45nm per il 2007
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
28
Inverter: caratteristiche dinamiche
Per
trovare
le
caratteristiche dinamiche è
necessario un modello
ancora più approfondito
dei transistor.
In prima approssimazione Vin
si può pensare che la
risposta sia influenzata da
una sola capacità che
rappresenta
tutte
le
capacità parassite e di
carico connesse sul nodo
di uscita
Inverter CMOS
Calcolo dei parametri dinamici
Università di Cagliari
Dipartimento di Ingegneria Elettrica ed Elettronica
Laboratorio di Elettronica (EOLAB)
10 Ottembre 2005
Inverter: tempo di propagazione
L’evoluzione del sistema è quella di un tipico sistema RC.
La tensione d’uscita avrà un andamento esponenziale
(parte da VDD) fino ad arrivare a 0. Il tempo di
propagazione è dato dal tempo che impiega un sistema del
primo ordine a raggiungere il 50% dell’escursione
Vout
RON
VDD
V (t ) = V e
out
CL
CL
Massimo Barbaro
30
Calcolo del tempo di propagazione
Un’approssimazione del tempo di propagazione si può
trovare col semplice modello ad interruttore:
Vout
ED - Inverter CMOS
Vout
−
t
RC
DD
t
Evidentemente è necessario avere un modello
ancora più dettagliato per avere informazioni
quantitative sul comportamento dinamico.
Il primo punto da focalizzare è il valore esatto
della capacità CL di carico: da quali capacità è
costituita e quanto valgono
Il secondo punto è identificare RON e,
successivamente, sostituirla con un modello più
concreto del MOS
tp= ln2 • RON CL=0.69 RON CL
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
31
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
32
Capacità parassite
Layout
Sovrapposizioni (overlap) fra gate/drain e gate/source: danno origine a 2
capacità proporzionali all’area di sovrapposizione
n+
n+
Capacità di giunzione del
diodo PN (due contributi:
area e perimetro). Le
stesse capacità sono
ovviamente
associate
anche al drain
10 Ottembre 2005
Capacità dell’ossido, fra
gate e canale (se esiste il
canale) altrimenti fra gate
e body
ED - Inverter CMOS
Massimo Barbaro
33
Il layout è una vista dall’alto della fetta di silicio
che consente di determinare dove verranno
realizzati i dispositivi
Ad ogni passo di processo è associato un
diverso layer (colore)
Rettangoli appartenenti a diversi layer
rappresentano, ad esempio, dove verranno
realizzati i gate di polisilicio, le diffusioni di drain
e source, le piste di metal e così via
Sul layout è possibile stimare le dimensioni e
quindi le capacità parassite associate
10 Ottembre 2005
Layout e capacità parassite
Area di source
AS=WZ
Si forma un
MOS per ogni
intersezione
fra poly e
L
diffusione
Poly
Diffusione n+
Metallo
Contatto
34
Tutte le capacità parassite sono non lineari, il
che vuole dire che non sono parametri costanti
del problema ma cambiano al cambiare delle
tensioni in gioco.
In particolare, il valore delle capacità connesse
al gate cambia a seconda della regione di
funzionamento del MOS
Perimetro di drain
PD=W+2Z
Area di gate
AG=WL
10 Ottembre 2005
Massimo Barbaro
Capacità parassite
W
Z
ED - Inverter CMOS
(non si computa il lato
che confina col canale)
ED - Inverter CMOS
Massimo Barbaro
35
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
36
Capacità di gate/canale (gate/body)
Cutoff: non esiste il canale quindi gate e source/drain
sono isolati, tutta la capacità dell’ossido (COXWL) è fra
gate e body
CGB=COXWL, Cgs=0, Cgd=0
Triodo: si è formato il canale che è omogeneamente
distribuito sotto tutto il gate. Il body è isolato dal gate
dalla presenza del canale, mentre la capacità dell’ossido
si suddivide equamente fra gate/drain e gate/source
Capacità di sovrapposizione (overlap)
CGB=0, Cgs=COXWL/2, Cgs=COXWL/2
Fra gate/drain e gate/source è sempre presente anche
la capacità dovuta alla sovrapposizione (overlap) del
gate di polisilicio con l’area di drain o gate. Tale capacità
è proporzionale alla larghezza del canale.
Le capacità parassite di overlap
sono proporzionali all’area di
sovrapposizione:
L
Saturazione: il canale si strozza quindi non c’è più
capacità fra gate e drain, la capacità dell’ossido solo in
parte si associa al source
CGB=0, Cgs=2/3 COXWL, Cgd=0
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
37
10 Ottembre 2005
Capacità di diffusione
ED - Inverter CMOS
Massimo Barbaro
38
AD=WZ, AS=WZ
PD=W+2Z, PS=W+2Z
Riassumendo, le capacità parassite di un MOS
sono:
G
CGS
CGD
S
D
I valori equivalenti delle due capacità sono dunque
W
Il parametro xd (quindi COV) è una
costante del processo quindi non
dipende dal progettista
Capacità parassite
La capacità di diffusione (di source e drain) è data da
due contributi: area e perimetro della diffusione. Tali
contributi sono non lineari (variano al variare della
tensione) ma possono essere sostituiti da due capacità
equivalenti costanti (nel range di tensioni di interesse)
L’area di source (drain) è proporzionale a W. Il perimetro
invece viene calcolato senza tenere conto del lato che
confina col canale
xd
CgsO=COXxdW=COVW
CgdO=COXxdW=COVW
CSB
CSB=Keq(CJ0AS+CJSW0PS)
CDB= Keq(CJ0AD+CJSW0PD)
I parametri CJ0 e CJSW0 sono costanti di tecnologia, Keq
dipende dal range di tensioni
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
39
CGB
CDB
B
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
40
Capacità parassite
Calcolo del tempo di propagazione
Cutoff
Triodo
Saturazione
CGB
COXWL
0
0
CGS
COVW
COXWL/2+ COVW
2/3COXWL+ COVW
CGD
COVW
COXWL/2+ COVW
COVW
Siamo ora in grado di stimare più dettagliatamente la
capacità di carico CL
Ma in quali condizioni andiamo a misurare il tempo di
propagazione? Ipotizziamo di avere come carico
dell’inverter la porta più semplice possibile (il caso
migliore), ossia l’inverter stesso
In tale situazione infatti il tempo di propagazione sarà il
migliore possibile, in tutti gli altri casi a carico maggiore
corrisponderà tp maggiore
Vout
CSB Keq(CJ0AS+CJSW0PS) Keq(CJ0AS+CJSW0PS) Keq(CJ0AS+CJSW0PS)
CDB Keq(CJ0AD+CJSW0PD) Keq(CJ0AD+CJSW0PD) Keq(CJ0AD+CJSW0PD)
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
41
10 Ottembre 2005
Calcolo di tp: capacità in gioco
Mp
CDBp
CGp2
Mp2
Vout
Vin
CGDp+CGDn
CDBn
CGSn+CGBn
10 Ottembre 2005
CW
Mn
ED - Inverter CMOS
Mn2
CGn2
Massimo Barbaro
ED - Inverter CMOS
Massimo Barbaro
42
Calcolo di tp: capacità in gioco
CGSp+CGBp
Carico
Vin
43
Le capacità CGSn+CGBn e CGSp+CGBp non hanno
influenza perché si suppone che il segnale in ingresso
vari istantaneamente (ci pensa il generatore di segnale)
Le capacità CDBn e CDBp sono capacità di diffusione
La capacità CW è la capacità associata alla metallo di
interconnessione fra i due inverter (spesso trascurabile)
Le capacità CGn2 e CGp2 contengono diversi contributi
(gate/bulk, gate/drain, gate/source) ma possono essere
approssimate con la sola capacità di ossido (COXWL)
La capacità CGDn+CGDn è l’unica che non sia connessa
direttamente fra il nodo d’uscita e la massa. Può essere
trasformata in una capacità fra nodo d’uscita e massa
applicando il teorema di Miller. Contiene solo il
contributo di overlap perché il PMOS e o NMOS sono
sempre prevalentemente o in saturazione o in cutoff
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
44
Teorema di Miller
Calcolo di CL
Il teorema di Miller afferma che, se fra il nodo V1 e V2
esiste il guadagno A è sempre possibile trasformare
un’ammettenza fra i due nodi con due ammettenze fra
ciascuno dei due nodi e massa di valore opportuno.
V1
Y
V1
V2
V2
E’ possibile a questo punto calcolare CL come la somma
di tutti i componenti connessi al nodo di uscita
C
Valore
CGDp
2COVWp
CGDn
2COVWn
Si usa il peso 2 per via
dell’effetto Miller
CDBp Keq(CJ0ADp+CJSW0PDp)
Yeq1=Y(1-A)
Yeq2=Y(1-1/A)
Nel caso dell’inverter il guadagno fra il nodo di ingresso
e quello di uscita può essere considerato pari a -1 nel
punto di commutazione quindi Yeq1=Yeq2=2Y
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
45
Calcolo del tempo di propagazione
Vout(t)
CL
10 Ottembre 2005
ED - Inverter CMOS
COXWpLp
CGn2
COXWnLn
10 Ottembre 2005
ED - Inverter CMOS
Relazione
tensione su CL
corrente-
Massimo Barbaro
I (t ) = C
D
Moltiplicando membro
a membro per dt,
dividendo per ID ed
integrando. Gli estremi
di
integrazione
derivano
dalla
definizione di tpLH
La corrente che
scorre attraverso
il PMOS deve
caricare fino al
valore VDD la
capacità CL
Massimo Barbaro
CGp2
46
Calcolo del tempo di propagazione
Per calcolare il tempo di propagazione LH facciamo
l’ipotesi che l’ingresso commuti istantaneamente da VDD
a 0. In tale caso si può affermare che lo NMOS si
spenga istantaneamente mentre il PMOS si accende
ID(t)
CDBn Keq(CJ0ADn+CJSW0PDn)
t
pLH
=C
dV (t )
dt
VDD / 2
∫
L 0
out
dV
I (V )
out
D
out
Il problema è che la corrente dipende dalla tensione.
L’integrale dovrebbe tenere conto della variazione di ID al
variare di Vout
47
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
48
Calcolo del tempo di propagazione
Calcolo del tempo di propagazione
Con 0<Vout<VDD/2 si può fare l’ipotesi semplificante che il
PMOS sia sempre in saturazione e quindi la sua corrente
sia costante
Stessi conti si possono fare per il tempo di propagazione
nella commutazione inversa (HL). Si ottiene (i due ritardi
sono uguali se kn=kp):
k
I = (V − | V |)
2
Corrente in saturazione
(VSG=VDD-VIN)
Sostituendo
nell’integrale
t
pLH
=
D
DD
t
Tp
L
DD
L
t =
2
DD
ED - Inverter CMOS
Tp
Massimo Barbaro
p
pHL
p
DD
49
10 Ottembre 2005
Diminuzione di tp
Aumento della tensione di alimentazione (in realtà
non è praticamente possibile agire su questo
parametro perché è fissato da motivazioni
tecnologiche e di processo)
Riduzione della CL (che significa ridurre al minimo le
dimensioni dei transistor)
Aumento di kp e kn che però è una soluzione solo
parziale perché comporta l’aumento delle capacità
parassite (sia quelle dovute alle diffusioni che,
soprattutto, quella di gate dell’inverter di carico) e
quindi l’aumento di CL
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
C
kV
(t
t
L
pHL
pLH
≈
pLH
L
p
DD
+t
2
C
kV
)
DD
1 1 C
≈ +
k k 2V
ED - Inverter CMOS
L
n
p
Massimo Barbaro
DD
50
Potenza dissipata
Le opzioni per la diminuzione del tempo di
propagazione sono:
≈
n
CV
C
≈
k (V − | V |) k V
p
10 Ottembre 2005
2
p
51
Le componenti del consumo di potenza sono 3:
Potenza statica: è quella dissipata quando l’inverter
ha ingresso costante, in condizioni di stabilità
Potenza dinamica dovuta a CL: è la potenza
consumata in commutazione, dovuta al fatto che in
corrispondenza di una variazione d’ingresso deve
avvenire una variazione dell’uscita che comporta la
carica e la scarica di CL
Potenza dinamica dovuta a correnti di cortocircuito: è la potenza che si dissipa in
commutazione quando, temporaneamente, si
creano percorsi conduttivi diretti fra alimentazione e
massa
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
52
Potenza statica
Potenza dinamica su CL
La dissipazione di potenza statica è praticamente nulla
ed è legata solo a due fenomeni: la corrente di leakage
attraverso i diodi parassiti e la corrente di sottosoglia dei
MOS.
Il vantaggio della tecnologia CMOS rispetto a tutte le
altre è proprio il fatto di avere una dissipazione statica
praticamente trascurabile
Ileakage=IS+ID
Pstat=IleakageVDD
ID
Diodi parassiti (formati dalle
sacche n+ e dal body e dalle
sacche p+ e dalla nwell)
IS
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
53
10 Ottembre 2005
Potenza dinamica su CL
out
Vin=0
VDD
VDD
10 Ottembre 2005
54
L’energia totale erogata dall’alimentazione per
caricare completamente CL è:
dV
E =CV ∫
dt =
dt
= C V ∫ dV = C V
∞
CL
E
Massimo Barbaro
L
Energia fornita dall’alimentazione
Non c’è percorso diretto
verso massa perché lo
NMOS è off
ED - Inverter CMOS
Energia erogata dall’alimentazione
dV (t )
i (t ) = C
dt
Vout
Ogni volta che CL viene caricata in una commutazione
LH una certa quantità di energia deve essere prelevata
dall’alimentazione.
Parte di questa energia viene immagazzinata su CL e
parte dissipata nel PMOS
Se la transizione dell’ingresso è istantanea, lo NMOS si
spegne istantaneamente ed il PMOS si accende
(inizialmente in saturazione)
Il PMOS carica CL fino al valore di VDD con la sua
corrente di drain che varia al variare di Vout
∞
= ∫ i (t )V dt
0
VDD
DD
Energia assorbita da CL
VDD
L
out
DD 0
VDD
L
DD 0
out
L
2
DD
∞
ECL = ∫0 iVDD (t )Vout (t )dt
ED - Inverter CMOS
Massimo Barbaro
55
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
56
Energia assorbita da CL
Transizione HL
L’energia totale assorbita da CL è pari alla metà
dell’energia erogata dall’alimentazione, questo
perché l’altra metà viene dissipata sul PMOS
dV
V dt =
E =C ∫
dt
CV
= C ∫ V dV =
2
∞
CL
out
VDD
L 0
10 Ottembre 2005
L
out
out
L 0
2
DD
out
ED - Inverter CMOS
Massimo Barbaro
57
10 Ottembre 2005
Potenza dinamica dissipata
Pdyn = CLVDD2/T = CLVDD2 f
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
ED - Inverter CMOS
Massimo Barbaro
58
Potenza dissipata: considerazioni
L’energia totale dissipata in una doppia
transizione (L->H->L) è data dalla somma di
quella dissipata sul PMOS e sul NMOS.
Tale energia è indipendente dalla resistenza dei
MOS
La potenza dissipata si ottiene dividendo
l’energia per il tempo impiegato dalla doppia
transizione (ossia moltiplicando per la frequenza
di commutazione)
Nella commutazione opposta (HL) il PMOS si
spegne e CL si scarica attraverso lo NMOS.
In questa situazione l’alimentazione non eroga
energia (perché non eroga corrente).
L’energia che era stata precedentemente
immagazzinata su CL viene dissipata sul NMOS
59
La frequenza f per cui viene moltiplicata
l’energia non è necessariamente uguale alla
frequenza di funzionamento del sistema
Non è infatti vero che ogni singolo gate commuti
alla frequenza del sistema (non tutti i gate
commutano contemporaneamente)
Questo fa sì che la frequenza effettiva da usare
nella formula sia da pesare con un coefficiente
moltiplicativo che deriva da considerazioni
statistiche sulla probabilità di commutazione di
vari gate
La formula ci dà il caso peggiore (worst case)
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
60
Potenza dinamica da cortocircuito
Potenza dissipata
Se la transizione dell’ingresso non è istantanea non è
più vero che uno solo fra il PMOS e lo NMOS è in
conduzione
Al variare della tensione di ingresso può capitare che i
due dispositivi siano accesi contemporaneamente
dando origine ad una corrente di cortocircuito (Ishort) che
dissipa potenza
Edp=VDDIpeak(tr+tf)/2
Pdp=Edp f= fVDDIpeak(tr+tf)/2
Vin
La potenza dissipata totale è data dalla somma
delle 3 componenti:
P = Pstat+Pdyn+Pdp =
= IleakageVDD+ CLVDD2f + fVDDIpeak(tr+tf)/2
In genere il contributo di Pdyn è quello
dominante
Ipeak
Ishort
tf
10 Ottembre 2005
tr
ED - Inverter CMOS
Massimo Barbaro
61
10 Ottembre 2005
Prodotto Potenza/Ritardo (PDP)
Il termine PDP dipende solo da alimentazione e
che
vanno
quindi
minimizzate
CL
contemporaneamente
ED - Inverter CMOS
Massimo Barbaro
Massimo Barbaro
62
Riassumendo
Un parametro fondamentale di una tecnologia è il
prodotto potenza/ritardo (Power Delay Product)
Nel caso CMOS si può ricavare dalla formula della
potenza, notando che la massima frequenza di
funzionamento è pari al tempo di propagazione (per
frequenze maggiori il segnale non riesce a propagarsi
prima che l’ingresso varii nuovamente), dunque,
trascurando i contributi di statica e di cortociruito:
PDP=Pdyntp=CLVDD2 f tp= CLVDD2 (1/tp) tp= CLVDD2
10 Ottembre 2005
ED - Inverter CMOS
63
L’inverter CMOS ha una VTC rigenerativa
VOH=VDD e VOL=0 (massimo swing di tensione fra i 2
simboli)
Se kp=kn la VTC è simmetrica e VM=VDD/2
Il tempo di propagazione è proporzionale a CL ed
inversamente proporzionale alla W dei transistor
La dissipazione di potenza statica è praticamente nulla
La dissipazione di potenza dinamica è proporzionale al
quadrato della tensione di alimentazione ed alla
frequenza di commutazione
In commutazione ci possono essere cortocircuiti
temporanei fra alimentazione e massa
Il PDP dipende solo da VDD e da CL
10 Ottembre 2005
ED - Inverter CMOS
Massimo Barbaro
64