LA SPETTROSCOPIA

G. Digilio - principi_v10 versione 6.0
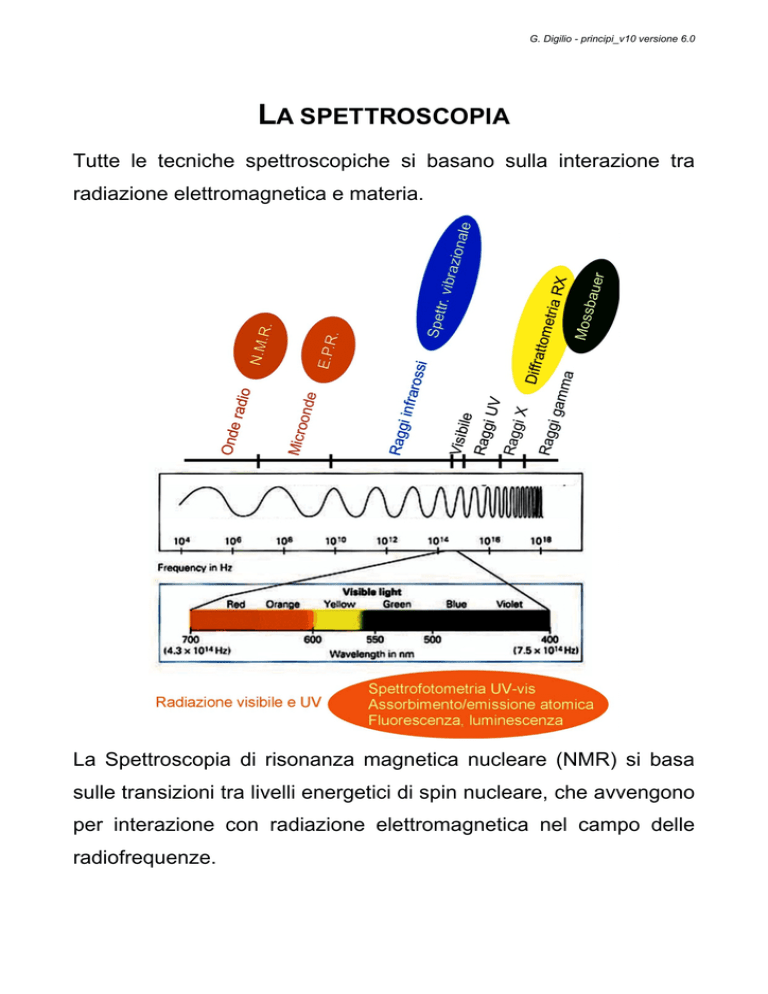
LA SPETTROSCOPIA
Tutte le tecniche spettroscopiche si basano sulla interazione tra
radiazione elettromagnetica e materia.
La Spettroscopia di risonanza magnetica nucleare (NMR) si basa
sulle transizioni tra livelli energetici di spin nucleare, che avvengono
per interazione con radiazione elettromagnetica nel campo delle
radiofrequenze.
principi_v10 versione 6.0
QUANTIZZAZIONE DEL MOMENTO ANGOLARE DI SPIN
Molti nuclei hanno un momento angolare di spin P . Secondo la
fisica classica un nucleo, assunto di forma sferica, ruota intorno ad
P
un asse.
Il momento angolare di spin è quantizzato (secondo le regole della
meccanica quantistica) e può assumere i valori:
P = I ( I + 1) ħ = h/2π
h = costante di Planck ( 6.6256 10-34 J.s)
I=
numero quantico del momento angolare (o, numero
quantico di spin, o semplicemente “spin nucleare”)
• Ogni nucleo è caratterizzato da un dato valore di I.
• I può assumere valori interi o semi-interi (I = 0, 1/2, 1, 3/2, 2
…6).
• Non è possibile calcolare I per un dato nucleo dalla teoria
principi_v10 versione 6.0
MOMENTO MAGNETICO
µ
Il momento angolare è associato con un momento magnetico µ
µ =γ P
dove
γ = rapporto giromagnetico (caratteristico di ogni nuclide)
Essendo quantizzato P, anche µ è quantizzato:
µ = γ I ( I + 1) Nella visione classica, un nucleo carico ruotando intorno al proprio
asse (moto di “spin”) genera un campo magnetico microscopico B
ed è equivalente ad una barretta magnetica il cui asse coincide con
l’asse di rotazione. Si parla cioè di “dipolo magnetico nucleare”.
principi_v10 versione 6.0
NUCLEI IMMERSI IN UN CAMPO MAGNETICO STATICO
1. QUANTIZZAZIONE DEL MOMENTO ANGOLARE
Un campo magnetico statico B0 introduce una direzione secondo
cui il momento angolare si orienta in modo che la sua componente
Pz lungo la direzione del campo assume un valore intero o semiintero (in unità di ħ). Pz è cioè quantizzata:
Pz = m ħ
m = numero quantico magnetico
m può assumere i valori: m= I, I-1, I-2,…, -I
• Ecco una rappresentazione grafica, molto intuitiva
I = 1/2
Ad esempio i nuclei:
1
H, 13C, 15N, 31P
I=1
Ad esempio i nuclei:
2
H, 14N
•
Di conseguenza, anche µz è quantizzato: µz
•
Il numero di orientazioni possibili di
µ
=mγħ
è 2I+1.
principi_v10 versione 6.0
NUCLEI IMMERSI IN UN CAMPO MAGNETICO STATICO
2. PRECESSIONE DI LARMOR
Nella meccanica classica la quantizzazione di µz è rappresentata
dal moto di precessione del dipolo nucleare (cioè del vettore
µ)
intorno alla direzione del campo magnetico statico B0.
La frequenza del moto di precessione dipende dall’intensità del
campo magnetico e dalle proprietà intrinseche del nuclide,
riassunte dalla costante γ (rapporto giromagnetico):
γ
B
ν =
2π
L
L’angolo tra la direzione B0 e quella di
0
µ,
se si tiene conto della
quantizzazione, può assumere solo alcuni valori (ad esempio, per
1
H che ha spin 1/2, θ= 54°44’).
principi_v10 versione 6.0
NUCLEI IMMERSI IN UN CAMPO MAGNETICO STATICO
3. QUANTIZZAZIONE DELL’ ENERGIA
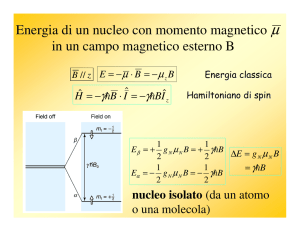
L’energia di un dipolo magnetico immerso in un campo magnetico
statico B0 è espressa da:
E = -µz B0 = - mγ ħB0
• Poiché Pz è quantizzato, anche E risulta quantizzato. Sono
possibili 2I+1 livelli energetici
I=½
I=1
• La differenza tra due livelli energetici adiacenti è:
∆E = Eβ – Eα = γ ħB0
• Regola di selezione: sono possibili solo le transizioni per cui
∆m = ±1
principi_v10 versione 6.0
POPOLAZIONE DEI LIVELLI ENERGETICI
LEGGE DI BOLTZMANN
La differenza di energia tra i due livelli di spin dipende dal campo
magnetico statico B0 :
Dato un insieme di spin equivalenti con I=1/2 essi si ripartiscono tra
lo stato α e lo stato β secondo la distribuzione di Boltzmann:
Nβ
Nα
=e
−
∆E
kBT
γ B0
∆E
≈1 −
=1 −
k BT
kB T
T= temperatura assoluta (K)
kB= costante di Boltzmann (1.3805 10-23 J K-1)
principi_v10 versione 6.0
POPOLAZIONE DEI LIVELLI ENERGETICI
LEGGE DI BOLTZMANN: ESEMPI NUMERICI
Dipendenza dal campo magnetico statico B0 della separazione dei
livelli energetici e della popolazione relativa degli stati α e β
(assumendo che la popolazione totale sia di due milioni di nuclei
equivalenti aventi spin 1/2)
Esempio numerico:
Nucleo: 1H (I=1/2)
B0=1.41 T
∆E= 2.4 10-2 J mol-1
T= 300K
Questo vuol dire che su 10 milioni di spin:
5.000.024 sono nello stato α
4.999.976 sono nello stato β
Nβ=0.9999904 Nα.
principi_v10 versione 6.0
MAGNETIZZAZIONE MACROSCOPICA (1)
• Consideriamo un insieme di N spin con I=1/2: in assenza di
campo magnetico il loro momento magnetico non si allinea
lungo alcuna direzione preferenziale
• In presenza di un campo magnetico statico si ripartiscono tra
lo stato α e lo stato β:
• Viene rispettata una distribuzione Boltzmaniana, per cui il
livello ad energia minore è più popolato:
principi_v10 versione 6.0
MAGNETIZZAZIONE MACROSCOPICA (2)
Immaginiamo ora di sovrapporre tutti gli N nuclei in un punto dello
spazio, da cui origina una terna di assi cartesiani, e di
rappresentarli semplicemente tramite il loro vettore
µ.
• La quantizzazione riguarda esclusivamente la componente di
µ
lungo la direzione di B0 (allineata con l’asse z), mentre
l’orientazione delle componenti di
µ
e lungo le direzioni x ed y
è casuale (e variabile, a causa della precessione di Larmor).
• La
sommatoria
vettoriale
rispetto
a
µ
definisce
magnetizzazione macroscopica M0.
N
∑ µ z = M 0 (Lo stato α è piu’ popolato di β)
N
N
∑ µx= ∑ µ y =0
(La componente di M0 sul piano xy è nulla!)
la
principi_v10 versione 6.0
L’ONDA ELETTROMAGNETICA
• Una onda elettromagnetica è costituita da un campo elettrico e
da un campo magnetico oscillanti ortogonali tra di loro che si
propagano nello spazio.
• Valgono le seguenti relazioni:
λ = c/ν
E = hν
• In un dato punto dello spazio, il campo magnetico oscillante può
essere rappresentato dalla somma vettoriale di due vettori
campo magnetico aventi intensità costante B1 e rotanti in senso
opposto.
principi_v10 versione 6.0
LA CONDIZIONE DI RISONANZA
• La condizione di risonanza si verifica quando l’ energia
associata con una onda elettromagnetica incidente è uguale
alla differenza di energia tra due livelli di spin contigui (cioè per
cui ∆m = ±1) .
∆E = Eβ – Eα = γħB0
Er.f. = hνr.f. (r.f.=radiofrequenza)
∆E = Er.f.
νr.f. = |γ/2π| B0
(o ωr.f. = |γ| B0)
NOTA: ωr.f. = 2πνr.f.
ωr.f. = velocità angolare (rad s-1)
νr.f. = frequenza (Hz o s-1)
• Equivalentemente, la condizione di risonanza è verificata
quando la frequenza dell’onda elettromagnetica incidente è
uguale alla frequenza di precessione di Larmor:
νLarmor = |γ/2π| B0
νr.f. = νLarmor
• Se la condizione di risonanza è soddisfatta, si verificano
transizioni tra livelli di spin con assorbimento netto di energia,
poiché in media ci saranno più transizioni α→β che β→α.
principi_v10 versione 6.0
LO SPETTROMETRO NMR IN ONDA CONTINUA
1946
Scoperta del fenomeno della risonanza magnetica
nucleare
fino al1972
Spettrometri ad onda continua (continuous wave, cw)
In alternativa, è possibile mantenere il campo magnetico statico
costante e variare la frequenza RF (“sweep” di frequenza)
Più è elevato il campo magnetico B0 più aumentano:
• sensibilità
• risoluzione spettrale
principi_v10 versione 6.0
L’ ESPERIMENTO NMR IN ONDA CONTINUA (CW)
1. Il campione viene immesso in un
campo magnetico di intensità
inizialmente bassa (B0iniz) e
sottoposto ad irradiazione R.F. a
frequenza fissa νRF.
2. Il campo magnetico
aumentato, lentamente.
3. Condizione di risonanza:
verifica un assorbimento
energia.
4. Il campo continua ad aumentare
fino al valore finale (B0fin)
∆E<Er.f.
∆E = Er.f.
si
di
viene
∆E<Er.f.
∆E>Er.f.
principi_v10 versione 6.0
RISONANZA E DISTRIBUZIONE DI BOLTZMANN.
SATURAZIONE
• All’ equilibrio termico un insieme di spin nucleari si ripartisce tra
gli stati α e β secondo la legge di Boltzmann (I=1/2 e γ>0):
E
β
α
• Irradiando con RF in risonanza, vengono promosse transizioni tra
livelli di spin. Le transizioni α→β e β→α sono equiprobabili.
Transizione α→β (bassa→alta energia): assorbimento energia
Transizione β→α (alta→bassa energia): emissione energia
• Lo stato α è più popolato: ci saranno più transizioni α→β che
β→α con assorbimento netto di energia. Tale assorbimento è
misurabile e dà origine al segnale NMR
• Se l’irradiazione continua (ed è abbastanza intensa), i livelli α e β
diventeranno equipopolati e non si osserverà più assorbimento di
energia: si giunge alla saturazione ed il segnale NMR scompare!
principi_v10 versione 6.0
LO SPOSTAMENTO CHIMICO (“CHEMICAL SHIFT”)
Sia dato uno spin immerso in un campo
…non è “solo”: è circondato dalla sua
magnetico esterno B0…
nube elettronica…
b
…la quale genera un proprio campo
…e c’è il resto della molecola, con i
magnetico…
suoi elettroni di legame e non…
Nuclei
te
non
chimicamenequivalenti
hanno frequenze di
Larmor generalmente
…ognuno dei quali produce un proprio
campo magnetico…
diverse.
principi_v10 versione 6.0
LO SPOSTAMENTO CHIMICO (“CHEMICAL SHIFT”)
La frequenza di precessione di Larmor di un dato spin dipende dal
suo intorno chimico, poiché esistono campi magnetici locali
microscopici BL che si sommano al campo magnetico esterno B0.
L’insieme dei campi magnetici locali BL schermano il nucleo di un
fattore σ (fattore di schermo) Il campo magnetico effettivo B0eff
sentito da un dato nucleo è dato da:
B0 = B0 (1-σ)
eff
ωLarmor= γ B0eff
principi_v10 versione 6.0
SPETTROSCOPIA 1H-NMR
B0eff= B0 (1-σ)
νLarmor= γ B0eff
HO-CH2-CH3
low
field
high
field
ωo
principi_v10 versione 6.0
CH3COCH2CH3
ESEMPIO DI SPETTRO 1H-NMR
principi_v10 versione 6.0
SENSIBILITÀ NMR DI UN NUCLIDE
L’intensità di un segnale NMR dipende fondamentalmente dalla
differenza di popolazione |Nα-Nβ|, che a sua volta dipende da γ, B0 e
T (legge di Boltzmann).
S NMR ∝ A
I +1
I2
γ 3 B30 / 2
dove A è l’abbondanza isotopica naturale del nuclide.
γ, sensibilità
15
N
2
H
50 77
13
31
125
202
C
P
1
H
500
Frequenza di Larmor, MHz
Per B0 = 11.75 T (Tesla)
E’ conveniente esprimere la sensibilità di un dato nuclide come
sensibilità relativa ad 1H
Proprietà NMR dei nuclidi più importanti
Nuclide
*
Spin
nucleare
(I)
Abbondanza
Sensibilità
Rapporto
Frequenza di
isotopica
relativa*
Larmor
[MHz]
giromagnetico γ
7
-1 -1
naturale
(10 rad T s ] (B0=2.3488 T)
[%]
1
H
1/2
99.985
1.00 RIF.
26.7519
100.00
2
-3
H
1
0.015
9.65 10
4.1066
15.351
6
Li
1
7.42
8.5 10-3
3.9371
14.716
11
B
3/2
80.42
0.17
8.5847
32.084
13
C
1/2
1.108
1.59 10-2
6.7283
25.144
14
-3
N
1
99.63
1.01 10
1.9338
7.224
15
N
1/2
0.37
1.04 10-3
-2.7126
10.133
17
O
5/2
0.037
2.91 10-2
-3.6280
13.557
19
F
1/2
100
0.83
25.1815
94.077
23
Na
3/2
100
9.25 10-2
7.0704
26.451
29
-3
Si
1/2
4.70
7.84 10
-5.3190
19.865
31
P
1/2
100
6.63 10-2
10.8394
40.481
57
-5
Fe
1/2
2.19
3.37 10
0.8687
3.231
119
Sn
1/2
8.58
5.18 10-2
-10.0318
37.272
195
Pt
1/2
33.8
9.94 10-3
5.8383
21.499
1
Sensibilità relativa al nucleo H a campo costante e per un numero uguale di nuclei.