Nomogramma
Da Wikipedia, l’enciclopedia libera.
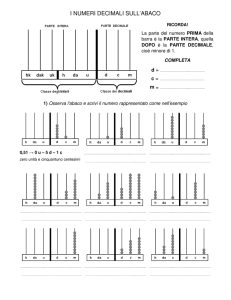
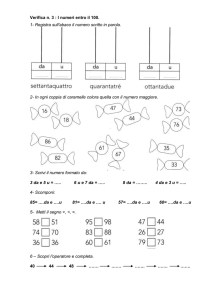
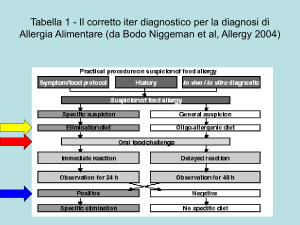
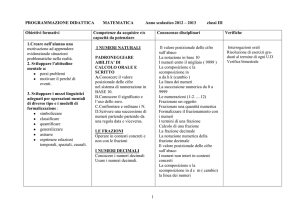
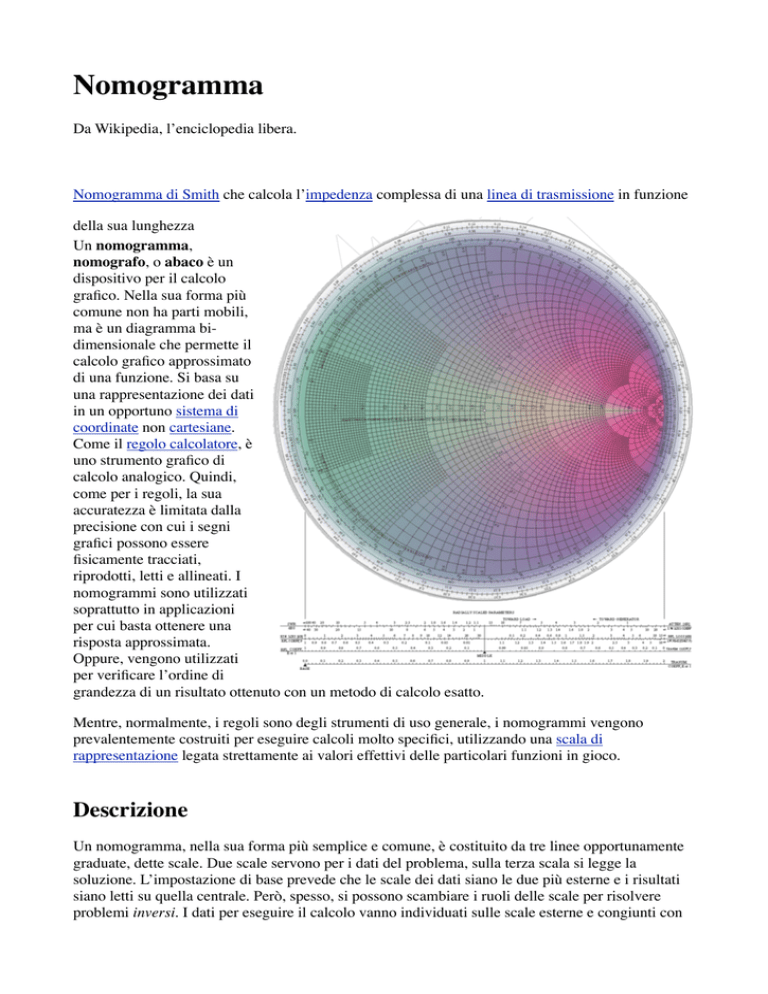
Nomogramma di Smith che calcola l’impedenza complessa di una linea di trasmissione in funzione
della sua lunghezza
Un nomogramma,
nomografo, o abaco è un
dispositivo per il calcolo
grafico. Nella sua forma più
comune non ha parti mobili,
ma è un diagramma bidimensionale che permette il
calcolo grafico approssimato
di una funzione. Si basa su
una rappresentazione dei dati
in un opportuno sistema di
coordinate non cartesiane.
Come il regolo calcolatore, è
uno strumento grafico di
calcolo analogico. Quindi,
come per i regoli, la sua
accuratezza è limitata dalla
precisione con cui i segni
grafici possono essere
fisicamente tracciati,
riprodotti, letti e allineati. I
nomogrammi sono utilizzati
soprattutto in applicazioni
per cui basta ottenere una
risposta approssimata.
Oppure, vengono utilizzati
per verificare l’ordine di
grandezza di un risultato ottenuto con un metodo di calcolo esatto.
Mentre, normalmente, i regoli sono degli strumenti di uso generale, i nomogrammi vengono
prevalentemente costruiti per eseguire calcoli molto specifici, utilizzando una scala di
rappresentazione legata strettamente ai valori effettivi delle particolari funzioni in gioco.
Descrizione
Un nomogramma, nella sua forma più semplice e comune, è costituito da tre linee opportunamente
graduate, dette scale. Due scale servono per i dati del problema, sulla terza scala si legge la
soluzione. L’impostazione di base prevede che le scale dei dati siano le due più esterne e i risultati
siano letti su quella centrale. Però, spesso, si possono scambiare i ruoli delle scale per risolvere
problemi inversi. I dati per eseguire il calcolo vanno individuati sulle scale esterne e congiunti con
una retta. Il punto in cui la retta interseca la scala centrale rappresenta il risultato. Sulle scale sono
segnate delle tacche ed evidenziati i valori più significativi per facilitare l’esatta collocazione dei
numeri. Le scale possono essere lineari, logaritmiche o avere una metrica più complicata. Per
calcoli relativamente semplici le scale sono riportate su delle linee rette ma, per calcoli più
complicati, è spesso opportuno o necessario utilizzare scale disposte lungo curve più o meno
semplici.
L’utilizzo è molto semplice, serve solo un righello o un filo teso. Basta posizionarlo in modo che
congiunga i punti che rappresentano i dati del problema su due scale e vedere dove interseca la terza
scala. Questo permette di calcolare una variabile a partire dalle altre due. A volte vengono
rappresentate delle curve aggiuntive che riportano i valori di una o più delle scale fondamentali in
una diversa unità di misura o sottoposti ad altre semplici trasformazioni.
Esempi
Nomogramma per le moltiplicazioni
L’esempio più banale di nomogramma è costituito da tre segmenti paralleli ed equidistanti che
riportano delle scale lineari. La retta che congiunge i punti a e b sui due assi esterni individua la
loro media (a + b) / 2 sull’asse centrale. Se alle scale lineari si sostituisce la stessa scala logaritmica
su tutti i segmenti, la stessa operazione fornisce , in quanto è la media tra log(a) e log(b) per le note
proprietà dei logaritmi. Se ora si sostituisce la scala logaritmica dell’asse centrale con una scala a
densità doppia, si ottiene il nomogramma rappresentato qui a fianco che calcola direttamente il
prodotto a * b. Questo semplice esempio mostra come, variando di poco la struttura del
nomogramma, si possono ottenere una grande varietà di strumenti di calcolo, solo molto
parzialmente rappresentati dagli esempi seguenti.
Nomogramma per resistenze in parallelo e lenti sottili
Nomogramma per resistenze in parallelo
Questo nomogramma serve per calcolare
Esso è interessante perché esegue un calcolo nonlineare utile nelle applicazioni utilizzando solo
linee rette con scale lineari.
A e B vengono segnati sulle scale orizzontale e verticale. Il risultato va letto sulla scala diagonale.
Siccome calcola una quantità proporzionale alla media armonica di A e B, questa formula ha molte
applicazioni. Alcuni esempi sono il calcolo delle resistenze in parallelo in elettronica e l’equazione
delle lenti sottili in ottica.
Nell’esempio a fianco, la riga rossa indica che due resistori da 56 e 42 ohm disposti in parallelo
producono una resistenza di 24 ohms. Ma indica anche che un oggetto posto alla distanza di 56 cm
da una lente la cui lunghezza focale è di 24 cm forma un’imagine reale alla distanza di 42 cm.
Nomogramma per il test Chi-quadro
Nomogramma per la variabile casuale chi quadro
Il nomogramma qui a fianco può essere usato per stimare alcuni valori necessari per eseguire un
comune test statistico, il test chi quadrato di Pearson. Questo nomogramma è un esempio di utilizzo
di scale curvilinee con graduazioni non equispaziate.
L’espressione da valutare è
La riga blu mostra come si calcola
(9 − 5)2/ 5 = 3,2
La riga rossa mostra come si calcola
(81 − 70)2 / 70 = 1,7
Nell’eseguire il test, si applica spesso la correzione di Yates per assicurare la continuità
ossia si sottrae 0,5 ai valori osservati. Si può facilmente costruire un nomogramma per eseguire il
test con la correzione di Yates. Basta spostare la scala dei valori osservati di 0,5 verso sinistra. Così
che le tacche relative ai valori 1.0, 2.0, 3.0, ... si trovino dove attualmente ci sono quelle dei valori
0.5, 1.5, 2.5, ...
•
•
Il nomogramma di Smith (cfr. immagine vicino al titolo), usato in elettronica e analisi dei
sistemi
I diagrammi termodinamici en:Thermodynamic diagrams e i tefigrammi en:Tephigram,
usati per studiare la struttura verticale dell’atmosfera e per eseguire calcoli sulla sua stabilità
e contenuto di umidità.
Bibliografia [modifica]
•
•
•
•
•
•
•
•
•
D’Ocagne M.: “Traité de Nomographie”, Gauthier-Villars, Paris, 1899.
D’Ocagne M.: “Sur la résolution nomographique de l’équation du septième degré.” Comptes
rendus Paris, 131 (1900), 522-524.
D’Ocagne, M.: Calcul graphique et nomographie. Doin. París, 1907. 3ª ed., 1924.
Brodetsky, S.: A first course in nomography. 1920.
Brodetsky, S.: artícolo Nomography in Glazebrook, R. (ed.): Dictionary of applied physics,
vol. III: 635. Macmillan and Co. London, 1923.
Parellada García, A.: Gráficas y nomogramas. Dossat. Madrid, 1942.
Seco de la Garza, R.: Nomogramas del ingeniero. P. Orrier. Madrid, 1911.
Soreau, R.: Nomographie. Théorie des abaques. Chiron. París, 1921.
Adams, D. P.: An index of Nomograms. M.I.T. e John Wiley & Sons, New York, 1950 Riferimenti bibliografici a migliaia di nomogrammi pubblicati su riviste.
Abaco
Da Wikipedia, l’enciclopedia libera.
Ricostruzione di un abaco di epoca romana realizzato
dal museo RGZ a Magonza nel 1977
L’abaco (sostantivo maschile) è un antico strumento di
calcolo, utilizzato come ausilio per effettuare
operazioni matematiche; È il primo strumento usato per
i calcoli sin dal 2000 a.C. in Cina e utilizzato in seguito
anche tra i Greci e i Romani.[1]
Etimologia
Il termine deriva dal latino abacus, tramite la forma
genitiva ἄβακας del greco ἄβαξ, che proviene a sua volta dall’ebraico חשבונייה, “polvere”.
Infatti il termine originario si riferiva ai primi abachi costituiti da una tavoletta di sabbia.[2]
Funzionamento
Un abaco, nella sua forma più comune, è costituito da una serie di guide (fili, scanalature, ...)
parallele, che convenzionalmente indicano le unità, le decine, le centinaia e così via. Lungo ogni
guida possono essere spostate delle pietruzze (dette calcoli, da cui il termine moderno di accezione
matematica) o altri oggetti mobili per eseguire le operazioni aritmetiche. I materiali usati per la
costruzione degli abachi e la loro foggia costruttiva variano moltissimo a seconda del luogo e
dell’epoca storica. Però il funzionamento si basa sempre sul principio fondamentale che il valore di
una configurazione di calculi dipende dal posto che occupa [3], ossia dalla guida su pui è
posizionata. Cioè le pietruzze su linee diverse indicano grandezze di ordine diverso, anche
frazionarie. Tale principio sarà poi alla base di ogni sistema di numerazione posizionale.
Le operazioni facilitate dall’uso dell’abaco non sono soltanto addizioni e sottrazioni, ma anche
moltiplicazioni e divisioni, viste rispettivamente come addizioni e sottrazioni ripetute. Inoltre,
grazie ad opportune configurazioni fisiche dello strumento e ad opportune tecniche, la velocità di
esecuzione dei calcoli può essere ragguardevole [4]. Tuttavia, l’abaco non può essere considerato
una calcolatrice meccanica in quanto non dispone di meccanismi. L’operatore deve eseguire
manualmente tutte le operazioni, nulla avviene in modo automatico.
Storia
L’abaco fu in uso in Europa a partire dai periodi degli antichi greci, come riferisce Erodoto (lo
stesso storico greco afferma come già gli egizi lo conoscessero); anche nella Roma antica si
impiegavano tali strumenti, usando tavolette di metallo con scanalature parallele su cui scorrevano
palline mobili oppure tavolette di legno coperte di sabbia.
L’uso dell’abaco in Europa durò a lungo: nel tardo Medioevo comparve un abaco a linee orizzontali
rappresentanti successive potenze di 10; questo strumento cessò di essere impiegato tra la fine del
XVII secolo e l’inizio del XVIII. Nelle immagini seguenti possiamo vedere diversi tipi di abachi
utilizzati in Europa nei secoli scorsi. Spesso non erano strumenti trasportabili, ma linee o riquadri
tracciati su un piano, dove venivano collocati e spostati dei gettoni. Il più famoso di questi fu
l’abaco a scacchiere, utilizzato nelle isole Britanniche, da cui deriva il titolo attribuito al ministro
delle finanze inglese: Cancelliere dello Scacchiere.
•
Nel Medioevo in Europa alla parola abaco si attribuiva solitamente il significato di aritmetica in
senso generale: a riprova di questo vi è il titolo di un importantissimo libro di Fibonacci: Liber
abbaci, pubblicato nel 1202.
Anche presso i popoli orientali erano in uso attrezzi simili: in Cina sono stati ritrovati abachi
risalenti al VI secolo a.C., che utilizzavano come calcoli bastoncini di bambù. Sempre in Asia, in
Corea, è rimasto, fino al XIX secolo, l’utilizzo di abachi di quest’ultimo tipo. Oltre alla Cina anche
in Giappone l’uso di questo strumento è durato a lungo nel tempo (più di quanto sia accaduto
nell’Occidente), tanto che ancora nella seconda metà del XX secolo molti negozianti giapponesi
utilizzavano un abaco per fare i conti. Nell’abaco giapponese la scanalatura è doppia: la parte
inferiore contiene quattro oggetti e quella superiore uno solo, facendo sì che le operazioni ricordino
in un certo senso quelle con i numeri romani.
Evoluzione dell’abaco è il pallottoliere, perfezionato dai romani che crearono così il primo
calcolatore tascabile fu un oggetto indispensabile per i romani ottenuto con grande successo.
L’abaco in tempi recenti
Ai giorni nostri l’abaco, tranne qualche eccezione nei paesi orientali, viene usato quasi
esclusivamente come gioco per bambini. Talvolta viene utilizzato in alcune scuole elementari per
insegnare ai bambini a contare e ad eseguire alcune semplici addizioni e sottrazioni.
A partire dai primi anni del XX secolo si è diffusa l’abitudine di usare il termine abaco, anche nella
variante abbaco, come sinonimo di nomogramma.
Scuola d’abaco
La parola “abaco”, in questo caso, assunse una definizione più vasta di quella originaria, e comprese
anche la disciplina, il testo scritto e la scuola, basti pensare ai modi di dire “andare all’abaco”.[5]
Nel periodo medievale e rinascimentale le scuole d’abaco furono i luoghi preposti per la formazione
dei tecnici. Fondate nel XIII secolo, per venire incontro alla necessità degli artigiani, dei mercanti,
dei tecnici e di altre categorie professionali, di istruirsi e di addestrarsi, sono equiparabili agli
odierni istituti professionali.
L’insegnamento era basato sulla matematica, spiegata con metodi applicativi; l’allievo, o meglio
dire l’apprendista, infatti, imparava tramite i metodi dell’osservazione e dell’esercitazione su
problemi congruenti al mestiere che stava imparando. I manuali scritti erano pochi, spesso
incompleti ed incomprensibili per un buon numero di apprendisti e redatti in lingua volgare.
Benché tra i meriti principali degli abachisti vi fosse l’introduzione delle cifre arabe e la diffusione
dell’algebra.[5], presto si verificò una contapposizione tra essi (legati alla notazione romana) e gli
algoritmisti, che propugnavano l’uso della nuova notazione. Si noti a questo proposito la prima
immagine della galleria, Typus Arithmeticae. Sotto l’egida dell’Aritmetica eseguono calcoli sia
Boezio (algoritmista) che Pitagora (abachista).