tensione tensione elettronico

Elementi di elettronica per Sensori
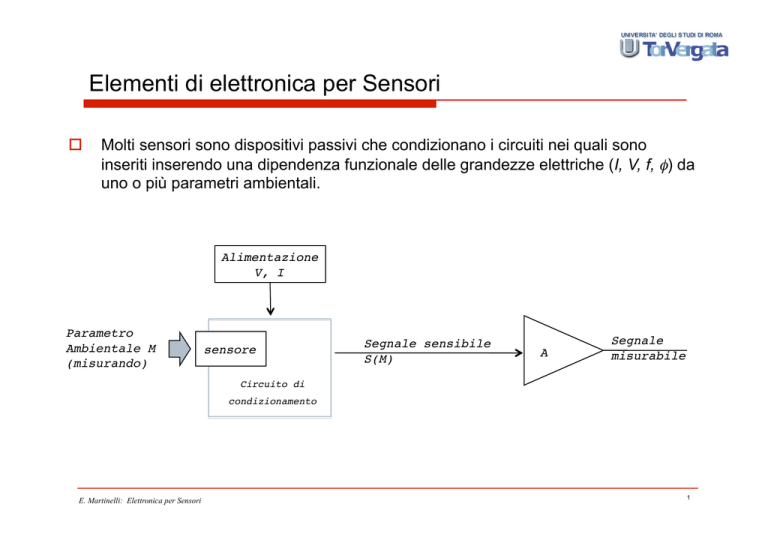
 Molti sensori sono dispositivi passivi che condizionano i circuiti nei quali sono
inseriti inserendo una dipendenza funzionale delle grandezze elettriche (I, V, f, φ) da
uno o più parametri ambientali.
Alimentazione
V, I
Parametro
Ambientale M
(misurando)
sensore
Segnale sensibile
S(M)
A
Segnale
misurabile
Circuito di
condizionamento
E. Martinelli: Elettronica per Sensori
1
Generatori di Tensione Continua
 I generatori di tensione continua sono utilizzati per:
 generare tensioni di riferimento; generare correnti di riferimento; polarizzare elementi
del circuito; definire punti di lavoro di dispositivi attivi; …
 Interrogare Sensori a variazione di Resistenza.
 Generatore Ideale di Tensione Continua
 Non idealità dei generatori reali di tensione continua:
 impedenza di uscita non nulla; rumore; drift (precisione limitata); accuratezza limitata
E. Martinelli: Elettronica per Sensori
2
Non idealità del generatore di tensione continua
 Il generatore di tensione ideale non può
esistere perché la sua esistenza
condurrebbe ad assurdi fisici (i generatori
di tensione reali devono avere impedenza
di uscita non nulla, rumore in uscita,
precisione e accuratezza limitate).
 Collegando in parallelo due generatori
ideali di tensione si contraddice la legge
di Kirchhoff alle tensioni.
 Per molte applicazioni i generatori di
tensione reali sono rappresentati dal
modello al primo ordine:
E. Martinelli: Elettronica per Sensori
≅
3
Impedenza d’uscita
 la tensione generata si ripartisce tra il carico e l’impedenza di uscita
Zout«Zload
 Un buon generatore di tensione deve avere impedenza di uscita molto piccola
(così la tensione sul carico è circa uguale alla tensione nominale
indipendentemente, entro certi limiti, dal carico stesso).
E. Martinelli: Elettronica per Sensori
4
Generatori di Tensione Continua
 Il diodo ha una caratteristica simile al generatore di tensione ideale.
 Nei circuiti elettronici i riferimenti di tensione sono:
 basati su diodi polarizzati direttamente
 basati su diodi Zener
 di tipo bandgap
Generatore ideale di Tensione
i
i
Diodo
v
v
E. Martinelli: Elettronica per Sensori
5
Il Diodo come generatore di tensione di riferimento
 Diodo in polarizzazione diretta
 Termicamente poco stabili
 Sensori di temperatura !
 Diodo in Breakdown
 Si può ottenere (variando opportunamente i profili di drogaggio) Vref
qualsiasi (2 ÷ 200 V )
 Quando Vref ≈ 6V si riesce ad avere TC ≈ 1ppm/°C (compensazione tra
effetto valanga ed effetto Zener)
 Tolleranza elevata sulla tensione di riferimento
E. Martinelli: Elettronica per Sensori
6
Generatore di tensione con diodo Zener
R
Iz
Vz
 Questo semplice circuito è sufficiente per la maggior parte
delle applicazioni.
 Con diodi Zener di buona qualità (Vref ≈6 volt), si ha TC
dell’ordine di qualche ppm/°C.
 Questo circuito è però sensibile alle variazioni della tensione di
alimentazione VCC (che ovviamente non è “stabilizzata”).
Le variazioni di R e di VCC si ripercuotono
in variazioni della retta di carico, e quindi di
Vz
i
-VCC
Vz
Nel carico scorre una
corrente pari a:
R
Iz
v
Iz
IL
-VCC/R
E. Martinelli: Elettronica per Sensori
7
Alimentatore Stabilizzato
 Molto spesso è necessario disporre di generatori di tensione continua capaci di
fornire correnti elevate.
 I circuiti visti finora sono in grado di generare tensioni continue sufficientemente
accurate per la maggior parte delle applicazioni, ma conservano le loro proprietà
solo se erogano correnti di intensità non troppo elevata.
R
Rload
La massima corrente che scorre su R deve essere minore di
VCC/R;
La massima corrente che può scorrere sul carico è quindi
minore di VCC/R;
La resistenza R non può essere scelta troppo piccola
per non deteriorare la capacità del diodo Zener di “regolare”
la tensione (al limite per R →0 la tensione di uscita è pari a
VCC, cioè alla tensione di alimentazione non stabilizzata)
Nel circuito in figura, usando VCC < 10 V, R = 1 kΩ, si ha Imax
< 10 mA.
E. Martinelli: Elettronica per Sensori
8
Generatori di Corrente Continua
 I generatori di corrente continua sono utilizzati per:
 generare correnti di riferimento; generare tensioni di riferimento; polarizzare elementi
del circuito; realizzare carichi attivi; definire punti di lavoro di dispositivi attivi; generare
rampe lineari di tensione; …
 Interrogare Sensori a variazione di Resistenza.
 Generatore Ideale di Corrente Continua
I0
ZLoad
 Non idealità dei generatori reali di corrente continua:
 impedenza di uscita finita; rumore; drift (precisione limitata); accuratezza limitata
E. Martinelli: Elettronica per Sensori
9
Non idealità del generatore di corrente continua
 Il generatore di corrente ideale non può esistere perché la
sua esistenza condurrebbe ad assurdi fisici (i generatori di
corrente reali devono avere impedenza di uscita finita,
rumore in uscita, precisione e accuratezza limitate).
 Collegando in serie due generatori ideali di corrente si
contraddice la legge di Kirchoff alle correnti.
 Per molte applicazioni i generatori di corrente reali possono
essere descritti dal semplice modello:
≅
E. Martinelli: Elettronica per Sensori
10
Impedenza d’uscita
 la corrente generata si ripartisce tra il carico e l’impedenza di uscita
I0
Zout»Zload
 Un buon generatore di corrente deve avere impedenza di uscita elevata (così che la
corrente sul carico sia circa uguale alla corrente nominale indipendentemente, entro
certi limiti, dal carico stesso).
E. Martinelli: Elettronica per Sensori
11
Generatori di Corrente e BJT
Generatore di Corrente Ideale
(impedenza d’uscita infinita)
Caratteristica d’uscita del BJT
impedenza di uscita “elevata”, cioè molto
maggiore dei normali carichi che devono
essere pilotati nei circuiti integrati
i
IC
v
VCE
-VEARLY
Valore tipico: 10 ÷ 100 kΩ
E. Martinelli: Elettronica per Sensori
12
BJT in zona attiva
 In generale un generatore di corrente reale,
progettato per erogare I=I0, può erogare I ≅ I0
solo se il carico è “adatto”.
 Equivalentemente, un generatore di corrente reale
eroga I ≅ I0 solo se la tensione ai capi del
generatore è compresa tra Vmin e Vmax
E. Martinelli: Elettronica per Sensori
i
Zona attiva
Vmin
Vmax
v
13
Amplificatori operazionali
Principali Caratteristiche
Ideale A=∞
Rin= ∞ Rout= 0 Iin=0 E. Martinelli: Elettronica per Sensori
Reale
A=104-106
Rin=106-1012 Ω
Rout=10-1000Ω
Iin=nA
uscita limitata a
+Vs -Vs
14
Op-amp con feedback
Vin
Vin
 La controreazione negativa limita il guadagno ed estende la banda
passante
 L’op amp ideale in equilibrio ha:
1. Le tensioni all’ingresso uguali (massa virtuale)
2. Corrente in ogni ingresso nulla.
E. Martinelli: Elettronica per Sensori
15
Amplificatore invertente
RF
Rin
Vin
Guadagno infinito
Rin
RF
Vin
E. Martinelli: Elettronica per Sensori
IF Iin
Vout
Vout
Guadagno finito A<∞
Vin
Rin
RF
Vout
V -
16
Amplificatore non-invertente
Vin
Vout
R1
R2
E. Martinelli: Elettronica per Sensori
17
Amplificatore differenziale
R2
I1 R1
I 2
V1
V2
Vout
R1
R2
Utilizziamo le due regole:
1 V-=V+
2 la corrente di ingresso è nulla
E. Martinelli: Elettronica per Sensori
18
Amplificatore per strumentazione
Analysis of the circuit in (a) assuming ideal op-amps
To make the gain variable, R1 is implemented
as the series combination of a fixed resister R1f
and a variable resistor R1v. Resistor R1f
ensures that the maximum available gain is
limited.
E. Martinelli: Elettronica per Sensori
19
Instrumentation amplifier
calcolo del guadagno
vo1
R 2
v 1
i
R 1
v 2
R 2
vo2
Di solito, R4=R3 quindi per R1=∞ si ottiene G=1
R1=0 non è una condizione possibile (v1=v2)
E. Martinelli: Elettronica per Sensori
20
E. Martinelli: Elettronica per Sensori
21
Generatori di Corrente con Op.Amp.
R
   La retroazione negativa dell’operazionale forza la tensione del
morsetto invertente ad essere molto vicino a massa;
la corrente IR è quindi circa Vin/R ;
la corrente IR viene interamente iniettata nel carico (impedenza
di ingresso dell’operazionale idealmente infinita).
Vantaggi
Svantaggi
semplice
elevatissima impedenza di uscita
ridottissimo offset del convertitore tensionecorrente
possibilità di alimentare il carico con correnti
positive o negative
non consente l’alimentazione di carichi
“grounded”
in un circuito integrato occupa un’area molto
maggiore di un semplice circuito del tipo current
mirror
E. Martinelli: Elettronica per Sensori
22
Howland Current Source
RA
R
RA
RA
zload
Vantaggi
RA
 L’uscita dell’amplificatore differenziale
(Ad = 1) è Vload-Vin.
 Sulla resistenza R scorre quindi
IR=(Vload-Vin - Vload)/R = -Vin/R
 La corrente IR viene interamente
iniettata nel carico (impedenza di
ingresso dell’operazionale idealmente
infinita).
elevatissima impedenza di uscita
ridottissimo offset del convertitore tensione-corrente
possibilità di alimentare il carico con correnti positive
o negative
possibilità di alimentare carichi “grounded”
E. Martinelli: Elettronica per Sensori
Svantaggi
in un circuito integrato occupa un’area
molto maggiore di un semplice circuito
del tipo current mirror
23
Misura di un sensore resistivo con partitore
ΔM → ΔR → ΔV
R = f (M)
V = f (R)
 Per misurare un sensore resistivo utilizziamo un circuito a partitore di
tensione.€
€
Esempio: RS è un sensore resistivo lineare
R
V
RS Vo
La relazione tra il segnale d’uscita e la variazione di R è
non lineare.
Se il sensore varia la sue resistenza linearmente rispetto
al misurando, il segnale di tensione misurabile è non
lineare rispetto al misurando.
E. Martinelli: Elettronica per Sensori
24
Misura di un sensore resistivo con partitore
 Quale è il valore di Rs che massimizza la sensibilità nell’intorno di δ=0?
E. Martinelli: Elettronica per Sensori
25
Misura di un sensore resistivo con partitore
R 0
V
E. Martinelli: Elettronica per Sensori
RSVo
26
lineare
 La non linearità deriva dal fatto che anche la corrente dipende da RS
 La relazione tra V0 e δ diventa lineare se R>>RS
RS ⋅ (1 + δ )
1+δ
=V ⋅
R + Ro ⋅ (1 + δ )
2 +δ
RS
R
V ⋅ Ro
Vo = V ⋅
⇒ R >> RS ⇒ Vo = V ⋅ S =
⋅ (1 + δ )
R + RS
R
R
dV V ⋅ Ro
V
SLIN = o =
; SNONLIN =
dδ
R
4
 Vn LIN = 4 ⋅ k ⋅ T ⋅ B ⋅ R0

Vn = 4 ⋅ k ⋅ T ⋅ B ⋅ Req ⇒ 
R0
V
=
4
⋅
k
⋅
T
⋅
B
⋅
 n NONLIN
2

Vo = V ⋅
δ LOD =
E. Martinelli: Elettronica per Sensori
€
δ LOD LIN
Vn
⇒
=
S
δ LOD NONLIN
V
4 ⋅ k ⋅ T ⋅ B ⋅ R0
2 R
⋅ 4 =
4 Ro
R V ⋅ Ro
4 ⋅ k ⋅T ⋅ B⋅ 0
R
2
27
 La condizione R>>RS deve valere per ogni valore di δ
 Esempio δ<10 R=200R0
1
non lineare
0.8
Vo
1
=
⋅ (1 + δ )
V 200
δ LOD LIN
δ LOD
NONLIN
€
==
2
200 = 35
4
V0/V
0.6
0.4
0.2
lineare
0
0
2
4
6
8
10
12
δ
E. Martinelli: Elettronica per Sensori
28
Il Ponte di Wheatstone
  Configurazione circuitale che consente di misurare il valore di una resistenza
attraverso una misura di zero
Una volta bilanciato il ponte consente di misurare la variazione di resistenza in uno o
più rami: sensori resisitivi
V
R 1
R 3
V 1
V 2
∆V
R 2
E. Martinelli: Elettronica per Sensori
R 4
Il ponte si dice bilanciato quando ∆V=0
Condizione ideale in quanto:
• non è possibile realizzare resistenze uguali
• rumore termico scorrelato.
29
Misura di un Sensore Resistivo
Supponiamo il ponte bilanciato, con R1=R2=R4=R, valore a riposo della resis
tenza del sensore.
Una delle resistenze è un sensore resistivo
δ: variazione relativa di R
V
R
R(1+δ)
La relazione tra ∆V e δ è non lineare
V1
V2
∆V
R
E. Martinelli: Elettronica per Sensori
R
Un parametro importante per valutare le prestazioni
del ponte è la Sensibilità definita
30
Configurazione del ponte con sensibilità massima:
caso con un sensore
V
R 1
R 2
V 1
V 2
R3o+∆R
 R 4
Il ponte è equilibrato con δ=0, quindi la condizione di massima
sensibilità si ottiene con R2=R4, quindi con R1=R3. In pratica si
usa porre R1=R2 =R4 =R3o
E. Martinelli: Elettronica per Sensori
31
Misura con due sensori “uguali”
 Le prestazioni del ponte migliorano utilizzando due sensori uguali e sottoposti alla stessa
sollecitazione
R
R(1+δ)
V 1
V 2
R(1+δ)
∆V
La relazione può essere linearizzata nel caso di
piccole variazioni di R
R
La Sensibilità è doppia
rispetto al caso con un
sensore
E. Martinelli: Elettronica per Sensori
32
Misura con due sensori sottoposti
a sollecitazioni opposte
 L’uso di due sensori di caratteristiche simmetriche consente di ottenere una
relazione input-output lineare.
 Sensori simmetrici sono molto difficili da ottenere:
 Esempio: termistori NTC: R ≈ T-α PTC: R ≈ α T
R
R(1+δ)
lineare
V 1
V 2
∆V
R
E. Martinelli: Elettronica per Sensori
R(1-δ)
La sensibilità è la stessa del ponte con due
sensori
33
Misure con sensori simmetrici:
caso con tre sensori 1
 Configurazioni con più sensori simmetrici conducono ad un aumento della
sensibilità del ponte.
R(1-δ)
R(1+δ)
V 1
V 2
∆V
R
E. Martinelli: Elettronica per Sensori
R(1-δ)
34
Misure con sensori simmetrici:
caso con tre sensori 2
R
V 2
R(1+δ)
E. Martinelli: Elettronica per Sensori
R(1+δ)
V 1
∆V
R(1-δ)
35
Misure con sensori simmetrici:
caso con quattro sensori
lineare
R(1-δ)
R(1+δ)
V 2
V 1
∆V
Sensibilità massima
R(1+δ)
E. Martinelli: Elettronica per Sensori
R(1-δ)
36
Confronto delle prestazioni
E. Martinelli: Elettronica per Sensori
37
Ponte a cinque terminali
R(1+δ)
R
V x
R
R
-
∆V
R
-
+
R
+
V x
R
R(1+δ)
R(1+δ)
V x
R
-
R/2
Vx/2
E. Martinelli: Elettronica per Sensori
+
38
Ponte a cinque terminali
calcolo della relazione input/output
R(1+δ)
V x
R
-
R/2
Vx/2
V u
A=∞
V x
+
R
R(1+δ)
V u
Vx/2
I 1
I 2
Sensibilità massima
Lineare
E. Martinelli: Elettronica per Sensori
39
Effetto della tensione di offset
V
R
R(1+δ)
Voff
-
∆V
+
V 1
V 2
R
R
Per valori piccoli di δ la stabilità della tensione
di offset diventa importante
E. Martinelli: Elettronica per Sensori
40
Alimentazione in corrente
I
R
R+∆R
Voff
V 1
-
∆V +
R
R
V 2
E. Martinelli: Elettronica per Sensori
Considerando nulla la corrente
in ingresso nell’op.amp si ha il
seguente partitore di corrente: 2R
I
2R+∆R
41
Alimentazione in corrente
corrente imposta da un op.amp
I
R
R+∆R
Voff
-
+
R
R
-
+
Rrif
Vrif
E. Martinelli: Elettronica per Sensori
42
Amplificatore LOCK-IN
1
S
A
3
2
4
fo
+
R+ΔR
-1
6
5
Valor
medio
t
Vrif
1
3
2
4-
t+π/2
5
6
43