Il teorema di Pitagora
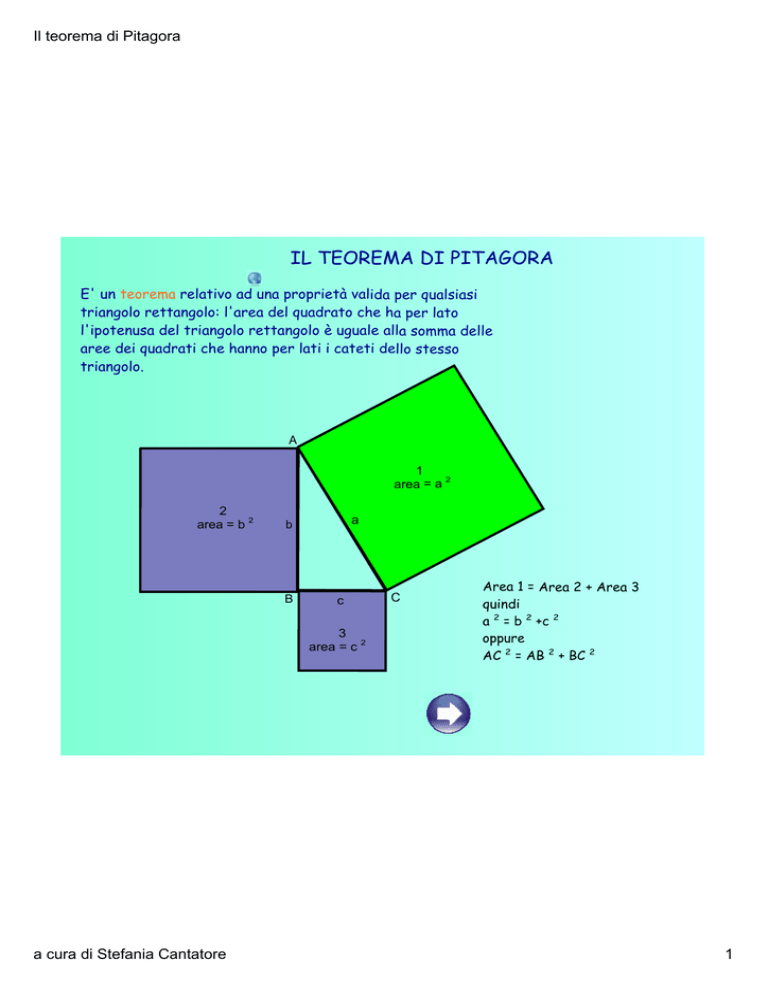
IL TEOREMA DI PITAGORA
E' un teorema relativo ad una proprietà valida per qualsiasi
triangolo rettangolo: l'area del quadrato che ha per lato
l'ipotenusa del triangolo rettangolo è uguale alla somma delle
aree dei quadrati che hanno per lati i cateti dello stesso
triangolo.
A
1
2
area = a 2
area = b 2
aa
b
B
c
3
area = c 2 a cura di Stefania Cantatore
C
Area 1 = Area 2 + Area 3
quindi
a 2 = b 2 +c 2
oppure
AC 2 = AB 2 + BC 2
1
Il teorema di Pitagora
DIMOSTRAZIONE GRAFICA
B
A
4
2
2
Q1
1
Q
4
1
3
a cura di Stefania Cantatore
3
Q
2
2
Il teorema di Pitagora
4
2
2
Q1
1
Q
4
1
Q
3
2
3
Si può notare che la figura A (quadrato A) è formata dal quadrato Q costruito sull'ipotenusa e dai triangoli
rettangoli segnati con 1 2 3 4, la figura B (quadrato B) è formata dai quadrati Q 1 e Q 2 costruiti sui cateti e dagli
stessi triangoli rettangoli segnati con 1 2 3 4.
Se eliminiamo sia dalla figura A, sia dalla figura B gli stessi triangoli (1 2 3 4) rimangono il quadrato Q e la somma dei
quadrati Q 1 e Q 2. Quindi il quadrato Q che ha per lato l'ipotenusa del triangolo rettangolo considerato è
equivalente (equiesteso) alla somma dei quadrati Q 1 e Q 2 che hanno per lati i cateti. a cura di Stefania Cantatore
3
Il teorema di Pitagora
B
b
c
C
A
a
QUINDI SI POSSONO RICAVARE LE SEGUENTI FORMULE:
a2=b2 +c2
a=
b2+c2
b2=a2-c2
b=
a2-c2
c2=a2-b2
c=
a2-b2
OPPURE:
2
= AB 2 + BC 2
AC =
AB 2 + BC 2
AB 2 = AC 2 - BC 2
AB =
AC 2 - BC 2
BC 2 = AC 2 - AB 2
BC =
AC 2 - AB 2
AC
a cura di Stefania Cantatore
4
Il teorema di Pitagora
b
c
a
Con i numeri:
a = 13 cm b = 12 cm
c = 5 cm
a 2 = 169 cm 2 b 2 = 144 cm 2 c 2 = 25 cm 2
2
a 2 = b 2 + c 2 = 144 + 25 = 169 cm I
b 2
16
I
II
III
IV
c 2
9
a
5
11
17
7
b 2 + c 2
25
b
4
8
15
5
a 2
25
c
3
7
8
4
T R SI/NO
SI
a cura di Stefania Cantatore
II
III
IV
5
Il teorema di Pitagora
Con il diagramma
b
c
*
*
b 2
c 2
+
a 2 = b 2 + c 2
a
a cura di Stefania Cantatore
6
Il teorema di Pitagora
Un teorema è una proposizione che esprime una proprietà che si
rende evidente, verificata, attraverso una apposita dimostrazione.
Un assioma o postulato è una proposizione che esprime una
proprietà che si considera palesemente, evidentemente vera e
che non deve essere (e non viene) dimostrata.
a cura di Stefania Cantatore
7
Il teorema di Pitagora
PROVA AD INDIVIDUARE E POSIZIONARE CORRETTAMENTE LE FORMULE PER IL CALCOLO
IPOTENUSA : c CATETO : a CATETO : b
Calcola l'ipotenusa
c c 2 ­ b 2 = a 2 Calcola un cateto
a
Calcola un cateto
b a 2 + b 2 = c 2 c 2 ­ a 2 = b 2
a cura di Stefania Cantatore
8
Il teorema di Pitagora
a cura di Stefania Cantatore
9