f ] 1 ,, . , , i
] . (
t ' t , I
)
::r
,
',- r'\
'.
',. 'L
1
SCUOLA
ESAME
GALILEIANA
DI STUDI SUPERIORI
DI AMMISSIONE.
-
CLASSE DI SCIENZE NATURALI
PROVA DI MATEMATICA
-
21 SETTEMBRE
2O1O
Il/La candidato/a deve svolgere, a sua scelta, non più di quattro dei sette esercizi che seguono.
Tutti gli esercizi hanno lo stesso valore in termini di valutazione.
Il/La candidato/a deve
indicare, apponendo una croce nelle apposite caselle, quali tra gli esercizi vuole vengano
considerati per la correzione. Esercizi che non siano chiaramente indicati in questa forma non
verranno presi in considerazione. Vengono valutate anche soluzioni parziali di esercizi.
AVVERTENZA:
Questo foglio deve essere consegnato assieme all'elaborato.
Esercizio l. Sia X un insieme di cardinalità n € N. Quante sono le coppie (Y, Z), LloveY e Z sorc
sottoinsìenridi X, tali c:heY a Z : 0 (insiemevuoto)/
Esercizio 2. Siano a, nt.e n numeri naturali strettamcntcnraggioridi l.
i) Si dirrrostriclrc sc p:
a'" - 1 è un rlunero primo, allora a:2
i i ) S i d i m o s t r ic h e s e q : a "
c rn è primo.
r è pari e n:2'con
+ 1 è u n n t t m c r op r i r r t o :, r l l o r : a
r natural.,.
E s e r c i z i o 3 . S i : rr r € N , z ) 1 c s i a n o0 < : r ' 1 < . . . ( n , , ( 1 . S i d i m o s t r ic h ee s i s t eu n r € [ 0 ,1 ] t a h c h e l a
L' : 1.... . ir, è ]. Irr altrc parole
rnediaaritnurticadcllc distanzerli .r'rla .r'1.,
'\_
nf"'
l r ' : r l' ' - i .
2
Quanti r con la proprietà surìdetta esistono'/
Esercizio 4. Sia /: A
, B un'applicazionetra .lue insiemi.
i)
Si dinostri chc l applicazionc/ è iniettiva se e solo se, per ogni coppia di sottoinsieiniX cY di A tali
cheXoY:0,siha/(X) n /(Y) -0.
ii I
Si dirlostri che l'applicazione / ò irriettiva sc c solo sc pcr ogni coppia di sottoinsiemi X e Y di ,4 si
h a/ ( x \ Y ) : / ( x ) \ / ( Y ) .
2
Esercizio 5. La sorgentedi un fascio di hrce l:r.scrè fissata ad un supporto circolare C di raggio 1, c(ìntrato
ncll'origine del piano. Il fàscio di luce ha origine dal punto di coordinate (r,y) : (t,0) ed ì: cLirr:tto
tangcnzialrnente a C, puntando nella direzione del semipiano {y > 0}. I supporto C può ruotarc iìttorrìo
all'origine. Si calcoli di che angoìo deve ruotarc il supporto C perchè il fascio di lucc colpisca urr punto di
coordinate(z,g), con z > 1 e y > 0.
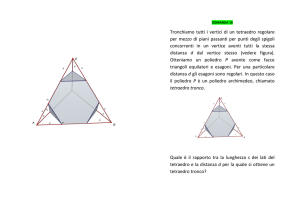
Esercizio 6. Un tetraedro si trova appoggiato su un piano con una certa laccia, gli vicrrt-'d:rto un colpo e
comincia a rotolarc. II rotolamento avviene per fàcce successivc,tutte equiprobabili.
i) Si calcoli la probabilità q", che il tetraedro torni a poggiare sulla laccia iniziale csattamente dopo n
rotolamenti (e urn prima).
ii) Si cal<:olila probabilità p,, che dopo rl rotolamenti il tetraedro torni a poggiare sulla laccia inizialc. E
possibile che tale probabilità sia nulla'/
iii) Si calcoli il numero medio di rotolanìenti nccessariaffincliè il tetràedro torni a poggiare sulla tàccia
iniziale (suggerìmento:può essercutile sapereche ![,
nr"-Ì :
ner lrl < t...).
6]y
Esercizio 7.
i) Si dirnostri che per ogni rrurneronnturale à ) 1 si ha
1 . r t + 2 . 2+!3 . 3 +! . . . + à À !: ( à + 1 ) ! - 1 .
ii) Si dimostri che ogni numero naturale n può esserescritto nella fbrma
n : c r . 1 !I q . 2 l i c a . 3 ! *
..lcn.hl ,
d.oveh, c1,c2,ca,.. ., c/r Sononumeri natur:ìli e cr < i per ogni I : 1, 2, . . ., h.
iii) Si dimostri Ie scrittura in ii) è essenzialrnenteunica nel scnsosegr.lente:se
n:
c r . l l l _ c 2. 2 1 +. j 3. 3 ! + . . . l c n . h \
:
! ...1,dt.!ll.
ù . 7 1 _ l d , z . 2*tr ] : t . 3 +
d o v cl ù , c 1 , c 2 , c a , . . . , c 6 , 1 , r f i , t 1 2 , d À ,s. .o.n, donl u r n e rni a t u r a l ic, i < i p e r o g n ii : 1 , 2 . . . . . h ,
Q { j
p c r o g n ij : 7 , 2 , . . . , t e h
( l , a l l o r ac i : ú l rp e r o g n ii - 7 , 2 . . . . , h e d ' - g p e r o g n l J -
h+7.h+2,...,t.