novembre 27, 2010
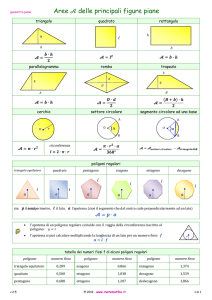
GEOMETRIA PIANA
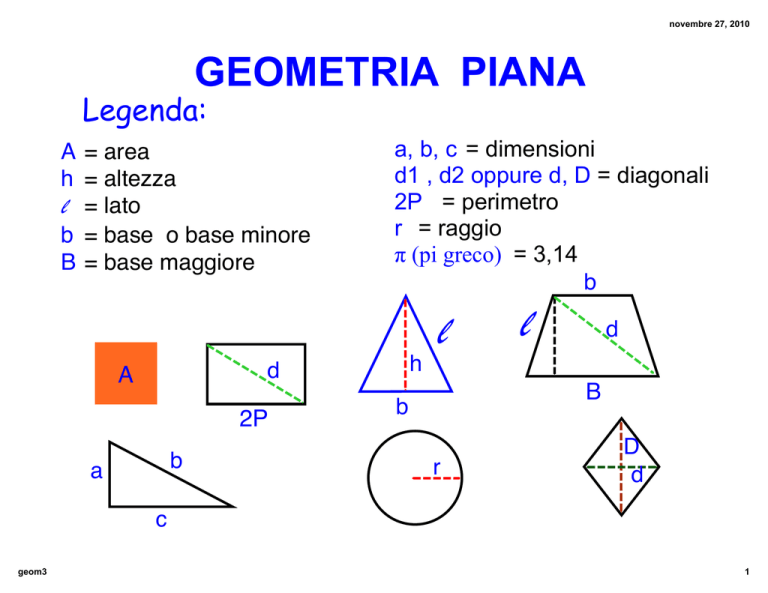
Legenda:
A
h
l
b
B
= area
= altezza
= lato
= base o base minore
= base maggiore
a, b, c = dimensioni
d1 , d2 oppure d, D = diagonali
2P = perimetro
r = raggio
π (pi greco) = 3,14
b
h
d
A
2P
b
a
l
l
d
B
b
r
D
d
c
geom3
1
novembre 27, 2010
Definizione
AREA
Significato
Esempio
spazio interno a un poligono
PERIMETRO misura del contorno di un poligono
EQUIVALENTI
stessa area
CONGRUENTI
uguali per forma e dimensioni
ISOPERIMETRICO
SIMILI
DIMENSIONI
Perimetro uguale
stessa forma ma grandezza diversa
base e altezza
h
b
LA GEOMETRIA PIANA HA 2 DIMENSIONI
geom3
2
novembre 27, 2010
PERIMETRO E AREA DEL TRIANGOLO
Il triangolo può essere considerato
la metà di un parallelogramma,
avente la stessa base e la stessa
altezza.
l
2P =
l
Equilatero
l
x
3
Isoscele
l
( x 2) + b
b
A
Scaleno
AB + BC + AC
C
geom3
A
A=bxh
2
h
C
b
B
B
3
novembre 27, 2010
FORMULE GEOMETRIA PIANA
Triangolo EQUILATERO
A=bxh
2
2P=l x 3
b=A x 2 : h
h=A x 2 : b
l = 2P:3
Triangolo ISOSCELE
A=bxh
2
2P=(l x 2)+b
l =2P-b:2
b=2P-(l x 2)
Triangolo SCALENO
A=bxh
2
2P=a+b+c
geom3
a=2P-(b+c)
4
novembre 27, 2010
PERIMETRO E AREA DEL QUADRATO
l
A=
lxl = l
l = √A
2
2P=l x 4
l = 2P:4
PERIMETRO E AREA DEL RETTANGOLO
A= b x h
h
2P=(b+h)x2
b
geom3
b=A : h
h=A : b
b=2P : 2 - h
h=2P : 2 - b
5
novembre 27, 2010
PERIMETRO E AREA DEL PARALLELOGRAMMA
b=2P : 2 b=A : h
A= b x h h=A : b
=2P : 2 - b
h
l
b
l
l
2P=(l+b)x2
PERIMETRO E AREA DEL ROMBO
l
d
D
geom3
A=Dxd
2
2P=l x 4
D=A x 2 : d
d=A x 2 : D
l = 2P:4
6
novembre 27, 2010
PERIMETRO E AREA DEL TRAPEZIO
A = (B+b)xh
2
Trapezio ISOSCELE
2P=(lx2)+B+b
Trapezio RETTANGOLO
2P=B+b+h+l
b=A x 2 : h - B
B=A x 2 : h - b
h=A x 2 - (B+b)
b=2P-(B-(lx2))
l =2P-(B+b):2
b=2P -(l+B+h)
l =2P-(B+b+h)
Trapezio SCALENO
c
geom3
2P=B+b+c+l
B=2P -(l+b+c)
c =2P-(l+b+B)
7
novembre 27, 2010
CIRCONFERENZA E CERCHIO
La circonferenza è una linea chiusa formata da punti
equidistanti da un punto interno (O) che si chiama CENTRO.
La distanza fra i punti e il centro si chiama RAGGIO.
O = centro
r = raggio
C = circonferenza
π
C
O
= 3,14
r
Il CERCHIO è la parte di piano
limitata da una circonferenza
r =√ A
π
C=2 π r r = C : (2 x π)
A=π r
X
X
geom3
2
X
8
novembre 27, 2010
FORMULE DIRETTE e INVERSE
Le formule dirette ci permettono di trovare area (A), circonferenza (C) o
perimetro (P)
Le formule inverse ci permettono di trovare uno dei dati usati nelle formule
dirette
Ad esempio, l’area del triangolo è: A = (b x h) : 2
Le formule per trovare la base e l’altezza sono: b= A x 2 : h h=A x 2 :b
Un piccolo trucco per trovare le formule inverse:
- scriviamo la formula partendo dal dato conosciuto (nel nostro caso A)
- scriviamo tutti i dati conosciuti della formula diretta partendo dall’ultimo
cambiando il segno dell’operatore
La sequenza è:
Formula
diretta
geom3
Formula
inversa
9
novembre 27, 2010
POLIGONI REGOLARI
I poligoni regolari hanno tutti i lati e tutti gli angoli congruenti
(equivalenti – uguali) perché:
- hanno i lati di uguale lunghezza
- hanno gli angoli di uguale ampiezza
PENTAGONO
OTTAGONO
TRIANGOLO
ESAGONO
QUADRATO
DECAGONO
2P =
geom3
l x numero di lati
10
novembre 27, 2010
AREA DI UN POLIGONO REGOLARE
a
a
a
a
a = APOTEMA
I poligoni regolari hanno TUTTI i lati e TUTTI gli angoli uguali.
Se unisci il centro del poligono con ogni vertice, dividi il poligono
in tanti triangoli congruenti quanti sono i suoi lati.
L'altezza di ogni triangolo si chiama APOTEMA.
A=
l
x
2
a
x
n° lati
A = px a
p=
2
numero fisso diverso
per ogni poligono
geom3
11
novembre 27, 2010
Apotema
Se si unisce il centro con i vertici, il poligono risulta diviso in tanti triangoli
congruenti (uguali). Il numero di questi triangoli è uguale al numero dei lati.
L’altezza di ogni triangolo corrisponde alla distanza tra il lato e il centro, e si
chiama apotema (a) del poligono.
a
AREA dei poligoni regolari
I poligoni regolari si possono dividere in tanti triangoli
quanti sono i lati.
Nell’esempio qui a fianco, l’esagono è stato diviso in 6
triangoli, coi quali è possibile formare un
parallelogramma con base la metà del perimetro del
poligono e con altezza l’altezza dell’apotema.
A = 2P : 2 x a (apotema)
geom3
12
novembre 27, 2010
AREA dei poligoni IRREGOLARI
Per calcolare l’area dei poligoni irregolari non esistono regole.
Conviene, quando è possibile, dividere la figura in altre conosciute
(quadrati, triangoli ecc;) e quindi calcolare e sommare le loro aree.
Nell’esempio a fianco abbiamo:
1 area del trapezio +
2 area del rettangolo +
3 area del quadrato +
4 area del rettangolo +
4 area del triangolo =
––––––––––––––––––
area del poligono irregolare
geom3
13