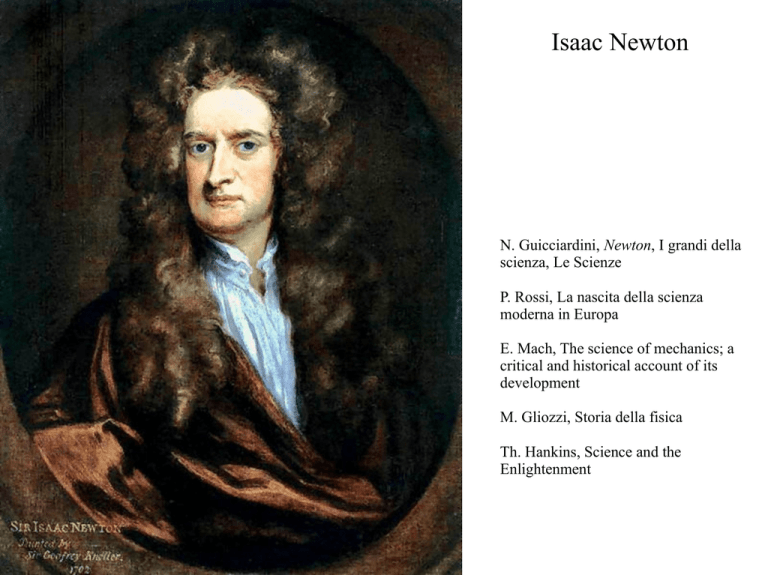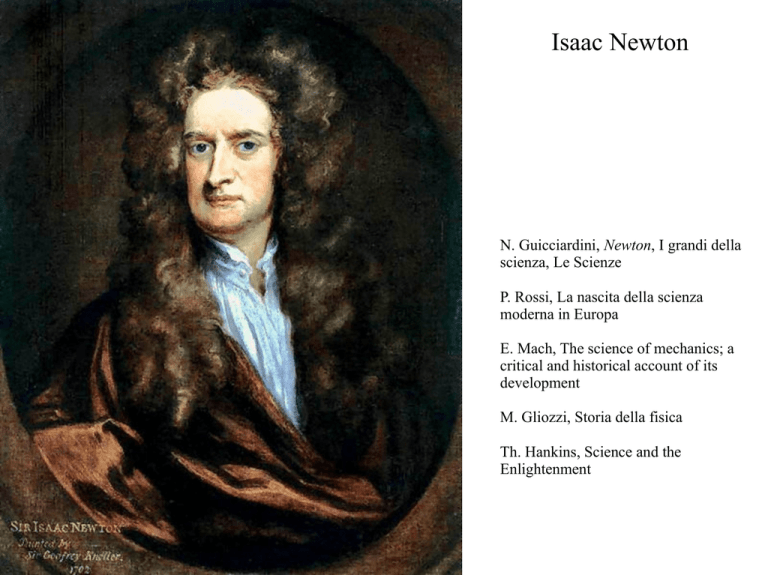
Isaac Newton
N. Guicciardini, Newton, I grandi della
scienza, Le Scienze
P. Rossi, La nascita della scienza
moderna in Europa
E. Mach, The science of mechanics; a
critical and historical account of its
development
M. Gliozzi, Storia della fisica
Th. Hankins, Science and the
Enlightenment
Cronologia
•
1642, 25 dicembre a Woolsthorpe, nel Lincolnshire (nota “polemica” di Robert Park...)
•
1661 entra al Trinity College di Cambridge come subsizar – legge Cartesio, Galileo
•
1665-1666 annus mirabilis, la “grande peste” di Londra → ritiro a Woolsthorpe.
Studi di ottica, matematica, gravitazione. Torna a Cambridge nel 1667.
•
1669 De Analysi, Lucasian Chair of Mathematics (Dirac, Hawking)
•
1672 Fellow della Royal Society; articolo sulla luce
•
1676-1680 lettere a Leibniz sul calcolo – corrispondenze con Hooke
•
1684 visita di Halley, comincia a lavorare ai Philosophiae Naturalis Principia Mathematica, pubblicati nel 1687
•
1689 parlamentare; esaurimento nervoso; per i successivi 35 anni si dà alla teologia
•
1696 Warden della Zecca
•
1699 inizia la disputa con Leibniz
•
1703-1727 presidente della Royal Society
•
1704 esce l'Opticks; in appendice il De Quadratura, prima vera pubblicazione sull'analisi
•
1705 nominato Sir
•
1727 muore, sepolto in Westminster Abbey, Londra
Le influenze filosofiche
•
Idea che lo accomuna ai rinascimentali (Bruno, Campanella): la verità è nascosta
nel passato e va cercata nei testi antichi, attraverso un'iniziazione; “la tesi di un
sapere segreto delle cose essenziali si configurò nella cultura europea come una
sorta di paradigma prevalente” “La diffusione del sapere, la discussione
pubblica delle teorie non sono state sempre avvertite come dei valori. Sono invece
diventate dei valori” (P. Rossi) (torre d'avorio vs. divulgazione; Newton vs.
Galileo) Convinzione di riscoprire una prisca sapientia nell'antichità egizia
•
L'”ultimo dei maghi”, definizione di J. M. Keynes
•
Cartesiano insoddisfatto: particelle + urti...., preoccupazioni teologiche
•
Cautamente baconiano, ma con contraddizioni importanti
•
Fervente anticattolico, è cristiano unitariano
La metodologia scientifica secondo Newton:
empirismo critico, metodo analitico-sintetico
Come in matematica, cosí nella filosofia naturale lo studio delle cose difficili mediante il metodo analitico deve sempre precedere
quello condotto con il metodo sintetico. Questa analisi consiste nel fare esperimenti ed osservazioni e trarre da questi,
mediante l’induzione, conclusioni generali, non ammettendo contro di esse delle obiezioni, a meno che non siano derivate
da esperimenti o da altre verità certe. Perché nella filosofia sperimentale non bisogna tener conto delle ipotesi. E
sebbene il trarre per induzione dei princípi generali dagli esperimenti e dalle osservazioni non equivalga a dimostrarli,
tuttavia è questo il modo migliore di ragionare che la natura consenta, e può considerarsi tanto piú saldo quanto piú
l’induzione sia generale. E se nessuna opposizione sorge dai fenomeni, si può pronunciare una conclusione universale.
Ma se in seguito sorgerà dagli esperimenti qualcosa di contrario, allora si dovrà affermare una conclusione che si
accordi con queste eccezioni. Mediante questa analisi possiamo procedere dalle cose composte alle cose semplici, dai
movimenti alle forze che li producono e in genere dagli effetti alle loro cause, dalle cause particolari a quelle piú generali, fino
a giungere alle cause generalissime. Questo è il metodo analitico; quello sintetico consiste nell’assumere come princípi le
cause scoperte e provate e, mediante queste, spiegare i fenomeni che ne derivano e provare tali spiegazioni
I. Newton, Ottica, Questione 31
La metodologia scientifica secondo Newton:
limitare le ipotesi (“regulae philosophandi” nei Principia)
“Delle cose naturali non devono essere ammesse cause più numerose di quelle che sono
vere e bastano a spiegare i fenomeni” (Principia, libro III)
idea di “semplicità della Natura, che non sovrabbonda di cause superflue e non fa nulla
invano”
→ rasoio di Occam, principio metodologico della parsimònia, della semplicità
“Perciò, finché può essere fatto, le medesime cause vanno assegnate ad effetti naturali
dello stesso genere” (Principia, libro III)
→ idea di uniformità della Natura, riduzionismo
Annus mirabilis
“All'inizio dell'anno 1665 trovai il Metodo di approssimazione delle serie e la Regola
per ridurre un qualunque esponente di un Binomio qualsiasi a tale serie. Lo stesso
anno in maggio trovai il metodo delle tangenti […] e in novembre avevo il metodo
diretto delle flussioni e l'anno successivo in gennaio la teoria dei colori e il maggio
seguente possedevo il Metodo inverso delle flussioni. E nello stesso anno cominciai a
pensare alla gravità che si estende all'orbita della Luna […] Tutto ciò avvenne nei
due anni della peste del 1665 e 1666, poiché in quei giorni ero nel fiore dell'età
creativa e attendevo alla Matematica e alla Filosofia più di quanto abbia mai fatto in
seguito.”
1665 - Il calcolo differenziale e integrale
•
FLUENTE → grandezza variabile (funzione del tempo)
•
FLUSSIONE → velocità istantanea di cambiamento della grandezza (derivata)
•
1) trovare la tangente ad una curva (trovare la flussione): uso dello sviluppo in
·
serie di potenze x → x+xo
(o = dt)
•
2) tabella FLUENTE → FLUSSIONI
•
3) inversione della tabella: FLUSSIONE → FLUENTE (integrazione)
•
NB: curve e non funzioni; usa infinitesimi invece che la procedura di passaggio al
limite; non c'è il rigore di concetti come continuità e differenziabilità, ecc., si
affida a “curve di generazione da moto continuo”
•
NB: 1665 → pubblica solo nel 1704 (probabilm. si sentiva inferiore rispetto agli
Antichi; reticenza e segretezza)
•
.
Polemica con Leibniz (si userà dx/dt al posto di ·x)
1665 - la scomposizione della luce
Cartesio: modello corpuscolare della luce: moto rettilineo, con rotazione
delle particelle più esterne del fascio dovuta all'interazione col prisma
(rifrazione)
Teorie
“modificazioniste”
della luce
Hooke: modello ondulatorio; i colori sono modificazioni della luce bianca
Tesi di Newton: il prisma non modifica ma separa; è la luce bianca ad essere quella più “complessa”
•
N.: - rifrange i singoli raggi colorati (allontana lo schermo dal prisma);
- “experimentum crucis” dei due prismi: rifocalizza la luce rifratta*
•
Nel 1668 costruirà un telescopio a riflessione (no aberrazione cromatica) → fellow della Royal Society,
1672 → segue articolo* su Transactions of the Royal Society, da cui nasce una bella discussione:
1. altri non riescono a replicare l'esperimento (mal descritto), e poi una sola falsificazione è poco (baconiani!)
2. Hooke: d'accordo, ma l'interpretazione è affrettata, “scomporre” è un modo di “modificare”
3. Huygens: poco interessante a proposito della natura della luce: cosa ci dice su onda o corpuscolo?
N. invoca “filosofi geometri” e “geometri filosofici”;
Luce bianca composta da corpuscoli con velocità differenti a
seconda del colore (blu più lenti → maggior deflessione)
La controversia lo turba, decide di
non pubblicare più alcunchè
“If he had encountered the sort of opposition with which
Galileo had to contend, it is probable that he would never
have published a line” (B. Russel)
Rifrattore di Hevelius, 140 piedi, 1650
La sfida di Wren a Halley e Hooke
→ Premio di 40 scellini a chi spiegasse il “sistema del mondo”
con una forza diretta verso il Sole e inversamente
proporzionale al quadrato della distanza
•
•
Halley si reca da Newton, agosto 1684
←
Risposta di Newton (ott.1684) : De motu corpu in gyrum
Cometa, 1682
→ Halley ne è entusiasta e sprona Newton.
•
Seguono 3 anni di lavoro intensissimo: i Principia
•
“Newton si lascia contagiare da quell'entusiasmo e si mette al lavoro con una
intensità che lascia sbalordito il suo assistente. Lavora senza sosta. Spesso scrive in
piedi, chino sul tavolo: anche il tempo per trovare una sedia o mangiare un boccone
gli sembra sprecato! Notti insonni e pasti saltati” (N. Guicciardini)
•
Halley finanzia, corregge, commenta, media (riconoscimenti per Hooke et al., Royal
Society più interessata a cose pratiche, baconiani...)
•
Libro difficile, scritto malissimo, circonvoluto.
Forze elastica di
Hooke: "ut tensio
sic vis"
I Principia: libro I: definizioni iniziali
•
Massa: densità x volume; distingue tra massa (la stessa in tutti i punti
dell'universo) e peso (dipende dalla gravità e varia con la distanza).
•
Quantità di moto: massa x velocità
•
Forza insita o innata, il perseverare di ogni corpo nel suo stato attuale, “questa
forza insita può essere chiamata con un nome più espressivo, forza di inerzia o
forza di inattività”, “a power of resisting”.
•
Forza impressa, azione esercitata su un corpo che gli fa cambiare il suo stato di
moto uniforme o di quiete.
•
Forza centripeta, quella per cui i corpi sono tirati verso un punto centrale (“of
this sort is gravity, by which bodies tend to the centre of the earth, magnetism, by
which iron tends to the loadstone; and that force, whatever it is, by which the
planets are perpetually drawn aside from the rectilinear motions, which
otherwise they would pursue, and made to revolve in curvilinear orbits”).
I Principia: libro I: i tre assiomi o leggi del moto
I. Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter...
Ciascun corpo persevera nel proprio stato di quiete o di moto rettilineo uniforme, eccetto
che sia costretto a mutare quello stato da forze impresse.
Esempi: moto di un proiettile, moto delle trottole, moto di rotazione sull'asse dei pianeti → N. non distingue inerzia da cons. mom. ang...
II. Mutationem motus proportionalem esse vi motrici impressae...
Il cambiamento di moto è proporzionale alla forza motrice impressa, ed avviene lungo la
linea retta secondo la quale la forza è stata impressa.
Non c'è F=ma (il senso è quello); N. non usa il calcolo delle flussioni, usa la geometria
III. Actioni contrariam semper & aequalem esse reactionem...
A ogni azione corrisponde una reazione uguale e contraria.
N. capisce che il Sole non è statico, ma subisce una piccola accelerazione
·
I Principia: II libro
Meccanica dei fluidi, acustica (undarum latitudinem, prima nozione di lunghezza d'onda)
I Principia: III libro, il “Sistema del mondo”
•
“Nei libri precedenti ho descritto […] principi non filosofici [ovvero fisici] ma
matematici […] Dagli stessi principi ora dimostrerò la struttura del sistema del mondo”
•
Premessa: regulae philosophandi
•
Le tre leggi di Keplero, in particolare orbite circolari, ellittiche, paraboliche o
iperboliche in presenza di forza centrale inversamente proporzionale a R².
•
mostra l'accordo tra le orbite e i calcoli, le maree come effetto della gravità, la
precessione degli equinozi, il moto delle comete, la legge della gravitazione universale.
Trova la stessa proporzione tra la gravità sulla Terra (caduta di un oggetto) e la forza che
lega la Luna (caduta della Luna,
scostamento dell'orbita dal moto rettilineo)→
philosophandi la forza nei due casi è sempre la stessa.
per la regula
III libro, prime dimostrazioni: generalizzazione della II legge di Keplero
Moto inerziale → AB=BC=CD...
Triangoli con stessa base e stessa altezza
→ area ∆OAB = area ∆OBC = area ∆OCD =...
Moto inerziale con impulso periodico verso
punto S →
N. dimostra che
area ∆SAB = area ∆SBC = area ∆SCD =...
Infine: spostamenti ridotti in infinitum →
traiettoria curvilinea
la gravitazione - 1. effetto di una forza centrale
•
Fino al 1680 N. non ne parla, anzi: idea di interazione locale, tramite un qualche mezzo interplanetario
→ inattendibilità del racconto della mela... (1665), ottiene comunque già un risultato notevole:
- Kepler:
T² = k R³
- Cartesio: corpo in moto circolare soggiace a due “conati” (moto tangenziale e “a recedere dal centro”);
N. ottiene (prima di Huygens?) a tal proposito:
(tendenza a recedere dal centro) è proporzionale a (v²/R)
(oggi: è l'accelerazione centripeta!);
E poiché
si ottiene
v = 2πR/T
(tendenza a recedere dal centro) è proporzionale a 1/R²
→ poiché i pianeti tendono a recedere dal centro dell'orbita ci deve essere dunque una forza che
controbilanci questa tendenza → forza va come 1/R²
N.B: in Cartesio mancava ancora tutta la dinamica, la distinzione tra sistemi inerziali e non... e la forza è
vista come una interazione di vortici
la gravitazione - 2. universalità dell'attrazione
→ tendenza a recedere:
F = mv²/R = m4π²/kR²
moltiplico e divido per un'altra massa (es. M Sole)
F = Mm4π²/MkR² = GMm/R²
con G = 4π²/Mk costante
Spazio e Tempo assoluti
Il tempo assoluto, vero, e matematico, in sé e per sua natura senza relazione ad alcunché di esterno, fluisce equalmente
senza relazione ad alcunché di esterno...
Lo spazio assoluto, per sua natura privo di relazione a qualcosa dii esterno, rimane sempre simile a sé stesso ed immobile
•
N. ritiene possibile parlare di un moto assoluto, in base agli effetti della rotazione (acqua che si solleva in un
secchio: allora l'acqua è ferma rispetto al secchio, ma in moto rispetto allo spazio assoluto; fune che si tende tra
due corpi)
•
“it is indeed a matter of great difficulty to discover and effectually to distinguish the true from the apparent
motions of particular bodies; for the parts of that immovable space in which bodies actually move, do not come
under the observation of our senses” (N.)
•
Motivazioni teologiche (“set” dell'intervento divino)
•
E. Mach: mostruosità concettuali : “No one is competent to predicate things about absolute space and absolute
motion; they are pure things of thought, pure mental constructs, that cannot be produced in experience. All our
principles of mechanics are, as we have shown in detail, experimental knowledge concerning the relative
positions and motions of bodies […] No one is warrented in extending these principles beyond the boundaries of
experience. In fact, such an extension is meaningless.”
(N.B.: Mach ispirerà il primo Einstein)
Ricezione, critiche e limiti dell'opera
•
Molte lodi, fonda la fisica matematica
1784: 40 libri su N. in inglese, 17 in francese, 3 in tedesco, 11 in latino, 1 in italiano
•
Supera di molto le prospettive poste dalla domanda di Halley; fertile, profondo
•
Supera troppo... (contesto assolutizzante, teologico)
•
Lavoro confuso e oscuro, e non solo secondo i canoni moderni
•
Usa la geometria invece del calcolo
•
F = ma (Eulero, 1750) verrà rivendicata come una nuova scoperta!
•
Idea imbarazzante della forza gravitazionale: a distanza ed istantanea
•
M. Gliozzi : “la sua opera è forse il più compiuto modello che abbia mai avuto la
fisica di armonica fusione di fatti sperimentali e di considerazioni teoriche”
(M.Gliozzi, Storia della fisica)
La critica di Mach: in Newton c'è parecchia metafisica!
Esempio: definizione di massa in Newton: “quantità di materia”
1) è tautologica! M = d V dove
d = M/V ....
2) più importante: è metafisica! Presupposto di esistenza di un qc. di esterno, mondo
in sé (Mach, positivista! Limitarsi a mettere in relazione i fenomeni, far
scomparire tutto ciò che è meta-fisico)
→ Mach dice: basta usare il 3 principio per la definizione di massa: tutto si riduce
ad una relazione tra corpi, come è giusto che sia sperimentalmente, nell'approccio
di M. non c'è assolutezza, solo relazioni
m2/m1 = a1/a2
Hypotheses non fingo
I have not as yet been able to discover the reason for these properties of gravity from
phenomena, and I do not feign hypotheses. For whatever is not deduced from the
phenomena must be called a hypothesis; and hypotheses, whether metaphysical or
physical, or based on occult qualities, or mechanical, have no place in experimental
philosophy. In this philosophy particular propositions are inferred from the
phenomena, and afterwards rendered general by induction.
Isaac Newton (1726). Philosophiae Naturalis Principia Mathematica, General Scholium.
d'altra parte...
“[By perfecting natural philosophy] the bounds of Moral Philosophy will also be
enlarged [and God's purpose will be exposed] by the light of Nature”. The discovery
of the laws of nature would necessarily lead to the discovery of God's intentions,
which formed the foundation of moral law.
(Hankins)
Il Newton ermetico
Tradizionale immagine di simbolo della Ragione (dipinto di Blake), Illuminismo, ma....
•
Dal 1668 legge e annota febbrilmente e ininterrottamente i testi della tradizione alchemica (Corpus hermeticus
di Ermete Trismegisto; Theatrum chemicum, Atalanta fugiens, Metamorphosis Planetarium...) esegue
esperienze sulla trasmutazione dei metalli; cerca risposte a domande quali “quali processi sono coinvolti nella
generazione di una pianta dal seme?”, “quali nel passaggio dalla volontà di muovere un braccio all'effettivo
movimento del braccio?” “Quali nella perdita di ordine di un organismo prima ordinato e animato?”
•
Idea di fondo: mondo non riducibile ad un meccanismo, c'è uno “spirito vegetativo”, una “virtù
fermentativa”; N. cerca di identificare le modalità di azione di Dio nella Natura, la “filosofia meccanica”
coglie solo una piccola parte dei fenomeni naturali
•
“A me par d'essere come un bimbo che gioca sulla spiaggia, e si rallegra se di quando in quando trova una
conchiglia più bella delle altre o un sasso più liscio degli altri, mentre il grande oceano della verità sorge
inesplorato dinanzi a lui”. ...Ecco cosa voleva dire N.!
•
Lettura e interpretazione della Bibbia, visto come testo da decifrare, simbologia numerologica
L'ultimo dei maghi o il grande ornamento dello spirito umano?
“I mortali possono gioire che sia esistito un tale e così grande ornamento dello spirito umano”
(epitaffio funebre)
“Nature and Nature's laws were hid in night
God said “Let Newton be”, and all was light.
(A. Pope, 1700 ca.)
“Mangia, beve e dorme? E' come gli altri uomini?”
(marchese de L'Hopital)
The more Newton's theological and alchemical, chronological and mythological work is examined as a whole
corpus, set by the side of his science, the more apparent it becomes that in his moments of grandeur he saw
himself as the last of the interpreters of God's will in actions, living on the fulfillment of times."
Es: moto inerziale tangenziale dei pianeti: dato da Dio affinché non
cadano verso il Sole in linea retta
F.E. Manuel, The Religion of Isaac Newton (Oxford 1974)
P. Rossi sul carattere contraddittorio di Newton: “La storia della rivoluzione scientifica e delle sue “torbide”
origini, può servire a renderci consapevoli che categorie come la razionalità, il rigore logico, la
controllabilità delle asserzioni, la pubblicità dei risultati e dei metodi che caratterizzano la struttura del
sapere scientifico non sono categorie perenni dello spirito né dati eterni della storia umana, ma conquiste
storiche che, come tutte le conquiste, sono suscettibili di andare perdute.”