Dispensa n. 7 del corso di
PLANETOLOGIA
(Prof. V. Orofino)
I CORPI MINORI DEL SISTEMA SOLARE:
ASTEROIDI
Università del Salento
Corso di Laurea Magistrale in Fisica
A.A. 2011-2012
Ultimo aggiornamento: Agosto 2011
1. Introduzione
Gli asteroidi (o pianetini) sono dei corpi minori del Sistema Solare formatisi
nella regione tra le orbite di Marte e di Giove e che sono pertanto essenzialmente
rocciosi. Essi sono alquanto importanti per gli studi sulla polvere presente nel Sistema
Solare in quanto, collidendo tra loro e con i meteoroidi, producono grandi quantità di
polvere interplanetaria. Gli asteroidi rivestono inoltre notevole importanza per gli
studi di meccanica celeste e sulla formazione del Sistema Solare.
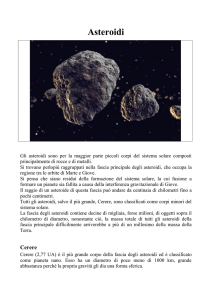
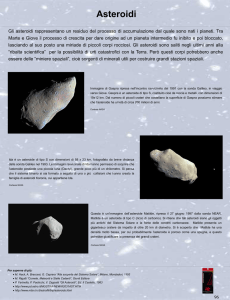
La fig. 1 mostra come un tipico asteroide appare quando è osservato con un
telescopio. L'immagine è stata ottenuta fotografando una regione di cielo con il
telescopio che si muove in modo da seguire perfettamente il moto apparente delle
stelle durante la posa. L’asteroide si rende facilmente riconoscibile dato che esso si
muove rispetto alle stelle, lasciando così una traccia rilevabile nell’immagine
risultante. Questo è il metodo col quale storicamente si sono scoperti gli asteroidi noti,
vale a dire rilevando il loro moto apparente sulla sfera celeste.
Fig. 1 Tre pose distinte e sovrapposte di uno stesso campo stellare ripreso mediante un telescopio.
Siccome il telescopio è dotato di un motore che gli permette di restare puntato sulla stessa zona di cielo,
compensando il moto di rotazione della Terra, gli oggetti fissi come le stelle appaiono sempre nella
stessa posizione in tutte le pose. Come l’immagine mostra in modo chiaro, oggetti asteroidali che si
trovino nel campo del telescopio si muovono invece in modo percettibile tra una posa e l’altra (da
Cellino et al., 2000).
2
Il fatto che gli asteroidi siano relativamente poco luminosi ed abbiano un
aspetto stellare spiega come mai nessuno di essi sia stato scoperto prima del 1801.
Anche facendo uso dei telescopi più potenti attualmente disponibili, infatti, gli
asteroidi rimangono in generale oggetti puntiformi che non mostrano un’estensione
apprezzabile. In realtà, come il termine “pianetini” lascia facilmente intendere, gli
asteroidi sono oggetti di dimensioni modeste; essi sono tutti privi di atmosfera che
non potrebbero comunque trattenere.
Il più grande oggetto conosciuto è anche il primo ad essere stato scoperto,
Cerere, ed ha un diametro di poco meno di 1000 km. Cerere è comunque molto
grande rispetto alla maggioranza della popolazione asteroidale, dato che solamente
una piccola minoranza di questi corpi può vantare dimensioni superiori a qualche
decina di chilometri.
2. La popolazione asteroidale
La stragrande maggioranza degli asteroidi, proprio come i primi oggetti
scoperti, orbita in una zona, la cosiddetta “Fascia Principale” (“Main Belt”), compresa
all’incirca tra 2.2 e 3.3 UA (v. fig. 2). Secondo recenti valutazioni, la Fascia
Principale conterrebbe circa 1 milione di oggetti con un diametro uguale o superiore a
1 km (Gribbin, 2004).
Fig. 2 – Proiezione sul piano dell’eclittica delle posizioni di un folto gruppo di asteroidi. Si osservano
la Fascia Principale e le orbite di quattro meteoriti originate da asteroidi collocati fuori dalla Fascia
Principale. Le due nubi di oggetti che seguono e precedono di 60 gradi la posizione di Giove
rappresentano i Troiani.
3
Al di fuori della Fascia Principale, esistono un centinaio di asteroidi che
orbitano più vicini al Sole, ad una distanza media di 1.9 UA (oggetti di tipo
“Hungaria”), come pure corpi posti a distanza maggiore dal Sole, ma sempre
internamente all’orbita di Giove (oggetti di tipo “Hilda” e “Thule”). Oltre a questi
esistono due grandi gruppi di asteroidi, con semiasse maggiore orbitale uguale a
quello di Giove. Si tratta dei due gruppi di asteroidi denominati “Troiani” che
praticamente si trovano sulla stessa orbita di Giove, formando insieme al Sole ed al
pianeta due triangoli equilateri: un gruppo precede Giove lungo l’orbita, mentre l’altro
lo segue (v. fig. 3). Questi punti sono soluzioni del cosiddetto “problema ristretto dei
tre corpi” studiato da Lagrange (v. par. 3 della Dispensa 2), il quale ha dimostrato che
un corpo di massa trascurabile, soggetto all’attrazione di altri due corpi C1 e C2 (in
questo caso il Sole e Giove), si trova in una posizione stabile rispetto agli altri due in
cinque particolari punti, due dei quali (detti “punti di librazione” L4 ed L5) coincidono
con i vertici dei due triangoli equilateri C1 L4 C2 e C1 L5 C2. Si pensa attualmente che i
Troiani siano molte centinaia di migliaia, per cui si tratta di un sottoinsieme cospicuo
dell’intera popolazione asteroidale.
Fig. 3 – Posizioni relative del Sole, di Giove e dei due gruppi di asteroidi Troiani.
Oltre agli asteroidi della cintura principale, agli oggetti Hungaria, Hilda, Thule
ed ai Troiani, esiste un’ulteriore sotto-popolazione asteroidale, e precisamente quella
che ha maggiore interesse dal punto di vista di eventuali impatti catastrofici che
4
possono coinvolgere il nostro pianeta. Si tratta degli oggetti le cui orbite si spingono
nella zona più interna del Sistema Solare fino in prossimità dell’orbita terrestre.
Questi oggetti sono stati convenzionalmente classificati in tre popolazioni che
prendono il nome di “Aten”, “Apollo” ed “Amor”.
I tre gruppi sono distinti in base ai parametri orbitali. In particolare, gli Aten
hanno un semiasse maggiore orbitale inferiore ad 1 UA, ma con distanza all’afelio (la
distanza massima dal Sole lungo l’orbita) maggiore della distanza media Terra-Sole.
Gli Aten sono dunque oggetti che spendono la maggior parte del periodo orbitale
all’interno dell’orbita terrestre, ma possono spingersi all’afelio ad una distanza che li
porta fuori dall’orbita della Terra. Gli oggetti Apollo, al contrario, sono caratterizzati
da un semiasse maggiore più grande di quello del nostro pianeta, ma con distanza al
perielio inferiore alla distanza media Terra-Sole. In questo caso, si tratta dunque di
oggetti che orbitano al di là dell’orbita terrestre per la maggior parte del tempo, ma
che ad ogni rivoluzione intorno al Sole si spingono per un tratto all’interno dell’orbita
della Terra. Gli Amor, infine, sono oggetti con orbite caratterizzate da una distanza
del perielio compresa tra 1.017 ed 1.3 UA. Si tratta cioè di oggetti che al perielio si
spingono nella zona compresa tra le orbite della Terra e di Marte.
Mentre a prima vista si potrebbe pensare che gli asteroidi Amor non
costituiscano un problema per la Terra, dato che essi (a differenza degli oggetti Aten
ed Apollo) non possono intersecarne l’orbita, la situazione è in realtà più complessa.
L’evoluzione dinamica di tutti gli oggetti Aten, Apollo ed Amor è eminentemente
“caotica”. Come vedremo al par. 4.4, ciò significa che questi asteroidi subiscono
evoluzioni orbitali su tempi relativamente brevi, per cui la distinzione tra i tre gruppi
risulta essere molto meno netta, e corrisponde solo ad una situazione transitoria.
Collettivamente, tutti gli oggetti che possono spingersi nelle zone dei pianeti
terrestri sono ora indicati con il termine di NEO (acronimo inglese dell’espressione
“Near-Earth Objects”, vale a dire oggetti vicini alla Terra). Ad oggi i NEO conosciuti
sono poche centinaia (Cellino et al., 2000). Occorre però ricordare che Rabinowitz et
al. (2000) hanno pubblicato un lavoro statistico che si basa sui risultati del programma
NEAT (Near Earth Asteroid Tracking) del JPL per l’individuazione automatica di
questi oggetti tramite un telescopio di 1 m sito alle Hawaii. Secondo questo studio la
popolazione totale di NEO con dimensioni superiori al chilometro conterebbe tra 500
e 1000 oggetti.
3 . Proprietà fisiche
Le informazioni che abbiamo sugli asteroidi si basano in massima parte su
tecniche indirette. Una tecnica molto importante è l’analisi delle curve di luce, ossia
dell’andamento temporale della luminosità di un asteroide. Due sono le cause per le
quali tale luminosità può variare nel tempo, ponendo costanti le distanze Sole5
asteroide e Terra-asteroide: una riflettività superficiale non uniforme oppure una
forma non sferica. Se l’oggetto è sferico ma “macchiato”, ossia con delle zone di
albedo diversa dalla media, la curva di luce (v. fig. 4a) è molto irregolare, con forti
variazioni collegate all’apparire e allo scomparire delle macchie; il ciclo completo
non ha in generale una forma simmetrica ed i massimi e minimi possono essere in
numero qualsiasi. Se l’oggetto ha un’albedo uniforme, ma non è sferico, esso ci
presenta una superficie apparente, e quindi una luminosità, continuamente diversa. Se
immaginiamo ad esempio un asteroide dalla forma ellissoidale con l’asse di rotazione
perpendicolare alla linea di vista, allora (v. fig. 4b) la curva di luce presenta un
alternarsi di due massimi e due minimi quando l’oggetto ci mostra rispettivamente il
suo lato “lungo” oppure il suo lato “corto”, il tutto con evidenti caratteristiche di
simmetria. Effettivamente le osservazioni sono per la stragrande maggioranza
conformi al secondo caso, indicando che gli asteroidi sono corpi essenzialmente non
sferici. In realtà si trovano entrambe le situazioni sopra descritte, ossia esistono corpi
allungati e macchiati contemporaneamente, ma la seconda caratteristica dà luogo a
variazioni di luminosità molto più piccole se paragonate con quelle dovute alla prima.
Fig. 4 Curve di luce ottenute nel caso di un corpo sferico “macchiato” (a) e di un corpo allungato
(b).
6
Altri dati molto importanti possono essere ottenuti per mezzo della cosiddetta
“tecnica radiometrica”. Tale metodo si basa sul fatto che, rispetto ad un corpo che
appare chiaro nel visibile, un corpo scuro delle stesse dimensioni sarà più caldo e
dunque più luminoso nell’infrarosso e contemporaneamente più debole nel visibile.
Pertanto la misura simultanea della radiazione solare riflessa da un asteroide alle
lunghezze d’onda della luce visibile e della radiazione termica che esso emette nella
regione del medio infrarosso consente di determinare contemporaneamente le
dimensioni e l’albedo (v. Appendice A per i dettagli).
La composizione degli asteroidi appare essere abbastanza eterogenea. In
assenza di campioni prelevati in loco, le attuali conoscenze si basano per lo più su
osservazioni spettroscopiche. Queste osservazioni hanno permesso di classificare gli
asteroidi in numerosi tipi tassonomici sulla base dei loro spettri in riflessione:
determinanti sono, in particolare, il livello del continuo (albedo) e la sua pendenza,
nonché la presenza di bande a certe lunghezze d'onda caratteristiche. La descrizione di
tali classi tassonomiche, riassunte schematicamente nell’Appendice B, esula dagli
scopi della presente dispensa. In questa sede val la pena soltanto di ricordare che la
classe C e la classe S sono le più numerose. Gli asteroidi di tipo C hanno albedo molto
bassa, usualmente compresa tra 0.05 e 0.1 (con minimi intorno a 0.02), e pertanto
dovrebbero essere di natura carbonacea (Cellino et al., 2000). Gli asteroidi di tipo S
hanno invece valori d’albedo diverse volte più alti di quelli degli asteroidi di tipo C e,
a causa delle loro caratteristiche spettrali, dovrebbero essere composti da silicati
(Cellino et al., 2000).
Occorre notare che asteroidi appartenenti alla stessa classe tassonomica non
solo hanno la stessa composizione, ma sembrano anche avere orbite simili intorno al
Sole (v. fig. 5). Così ad esempio la distribuzione dei semiassi maggiori delle orbite
degli asteroidi di tipo S ha un massimo tra 2 e 2.5 UA dal Sole che cade in prossimità
del bordo interno della Fascia Principale. Gli asteroidi C orbitano, invece, più lontano
dal Sole, dal momento che la loro distribuzione picca a circa 3.1 UA.
Una importante classe di asteroidi, quelli di tipo M, sembra esibire un
comportamento spettrale che suggerisce la presenza di grandi quantità di metallo
(ferro e nichel), il che indicherebbe che questi oggetti siano i nuclei metallici di corpi
progenitori differenziati, proprio come dei “pianeti in miniatura” (Cellino et al., 2000).
Il mantello e la crosta di questi oggetti progenitori sarebbero stati erosi nel tempo e
completamente rimossi da collisioni catastrofiche subite nel corso della loro storia.
Oggi sappiamo infatti che gli asteroidi hanno subito nel tempo un’evoluzione
determinata essenzialmente dalle collisioni. Ciò è testimoniato dalle immagini delle
superfici fortemente craterizzate degli asteroidi 243 Ida, 951 Gaspra, 253 Matilde, 433
Eros, osservati in anni recenti dalle sonde spaziali Galileo e NEAR.
7
Fig. 5 Distribuzione, in funzione della distanza eliocentrica, delle diverse classi spettrali di asteroidi
(modificata a partire dalla figura originale in Jessberger, 1991).
Esistono gruppi di oggetti che sono certamente da considerare come i
frammenti della distruzione di un certo numero di corpi progenitori. Questi gruppi
prendono il nome di “famiglie dinamiche” e sono caratterizzati dal fatto di
condividere in larga parte semiasse maggiore, eccentricità ed inclinazione orbitali
ereditati dal corpo progenitore.
4. Relazioni tra asteroidi e meteoriti
L’associazione tra meteoriti ed asteroidi, suggerita già diverso tempo fa, è
evidente negli spettri mostrati in fig. 6: gli asteroidi di tipo C dovrebbero essere
associati alle meteoriti della classe delle condriti carbonacee; gli asteroidi di tipo S
sarebbero invece imparentati agli altri aeroliti (soprattutto acondriti); gli asteroidi M
originerebbero le meteoriti ferrose, e così via per i tipi meno comuni.
A questo schema manca, però, un tassello importante; non c’è un’origine
ovvia per le condriti ordinarie, il tipo più comune di meteoriti. Questo rebus è ancora
oggi una delle questioni più aperte ed appassionanti: quali oggetti sono in grado di
produrre condriti ordinarie, se soltanto pochissime mostrano lo stesso colore? Una
delle soluzioni proposte è che in realtà le condriti ordinarie provengano da asteroidi di
tipo S, i più comuni nella regione interna della fascia asteroidale. Il fatto che le
meteoriti siano di colore neutro, mentre lo spettro degli asteroidi S mostra una
predominanza di rosso, sarebbe solo il risultato del cosiddetto “invecchiamento
spaziale”, dovuto all’azione di raggi cosmici ed agli impatti di micrometeoriti, che
tenderebbero ad alterare le superfici degli S facendoli diventare sempre più rossi col
passare del tempo (Cellino et al., 2000). Poiché gli oggetti piccoli sono probabilmente
8
frammenti provenienti da corpi grandi, si può anche ipotizzare che i primi presentino
delle superfici esposte che hanno subito un invecchiamento ridotto rispetto ai secondi.
Recenti osservazioni nel visibile sembrano mostrare infatti che i piccoli asteroidi S
hanno spettri molto più simili alle condriti ordinarie rispetto agli oggetti S di maggiori
dimensioni. Tuttavia prima di trarre conclusioni definitive occorre estendere
l’intervallo d’osservazione almeno fino al vicino infrarosso.
Fig. 6 Spettri di riflettività di alcuni asteroidi confrontati con spettri tipici di alcune classi di
meteoriti. Per evitare confusione i diversi spettri sono stati traslati arbitrariamente lungo l’asse
verticale. La grande similarità tra gli spettri degli asteroidi e quelli delle meteoriti suggerisce che queste
ultime abbiano avuto origine dai primi (da Chapman, 1975).
Come già osservato al par. 3, tutte le meteoriti di cui si è potuto determinare le
traiettorie hanno orbite simili a quelle seguite da molti asteroidi NEO. Questo sembra
suggerire che tali corpi non provengano da asteroidi orbitanti nella Fascia Principale
ma si siano invece staccati dai NEO (Cellino et al., 2000). Questa conclusione è anche
in accordo con i dati relativi alla durata dell’esposizione delle meteoriti ai raggi
9
cosmici. Si immagini il meteoroide incluso all'interno del corpo progenitore. Se esso è
sepolto ad una profondità sufficiente (pochi metri) riceverà una dose molto bassa di
raggi cosmici. Nel momento in cui un urto lo libera, esso inizia invece ad
immagazzinarne gli effetti. Il processo ha termine quando l’oggetto giunge sulla
Terra. Qui il bombardamento di raggi cosmici si arresta di nuovo. Come un
cronometro che blocca le sue lancette, così la dose di radiazione cosmica assorbita
dalla meteorite può essere “letta” dai ricercatori per determinare quanto è durato il
viaggio dal corpo progenitore al nostro pianeta. I tempi così stimati sono dell’ordine,
in generale, di l0 o 20 milioni di anni. Questi tempi sono più lunghi di quelli tipici
impiegati per giungere direttamente alla Terra a partire dalla Fascia Principale. Altri
meccanismi devono quindi essere invocati, come ad esempio la genesi a partire da
piccoli asteroidi NEO. In tal caso le future meteoriti non sarebbero seppellite in
profondità nell’asteroide progenitore, e inizierebbero ad accumulare gli effetti dei
raggi cosmici già ben prima dell’impatto che poi le libera (Cellino et al., 2000).
5. Evoluzione dinamica
All’interno della Fascia Principale, gli asteroidi non sono distribuiti in modo
omogeneo. Se si guarda infatti la distribuzione dei semiassi maggiori delle orbite degli
oggetti della fascia si può facilmente notare che esiste un certo numero di lacune (che
prendono il nome di lacune di Kirkwood), cioè valori del semiasse maggiore che
appaiono essere “proibiti”, nel senso che non corrispondono al semiasse orbitale di
alcun asteroide reale osservabile (v. fig. 7).
Fig. 7 – Distribuzione del numero dì asteroidi noti in funzione del semiasse maggiore dell’orbita. I
numeri in alto indicano le principali risonanze di moto medio con Giove, che corrispondono ad una
serie di valori proibiti del semiasse maggiore noti col nome di lacune di Kirkwood (dal sito web
http://spaceguard.esa.int/NScience/neo/images).
10
Per capire questa situazione occorre osservare che gli asteroidi risentono
fortemente delle perturbazioni gravitazionali dei pianeti, in particolar modo di Giove,
per cui le loro orbite sono soggette a continui cambiamenti. Le zone della Fascia
Principale prossime alle lacune di Kirkwood corrispondono ad orbite fortemente
caotiche. Un’orbita caotica è altamente instabile e non consente di effettuare una
predizione precisa della posizione dell’oggetto se non su intervalli di tempo più o
meno limitati.
Nel caso della Fascia Principale, il caos si instaura in modo imponente in
corrispondenza di certi tipi di orbite, a causa di fenomeni di risonanza. In particolare,
le lacune di Kirkwood nella Fascia Principale corrispondono a valori del semiasse
maggiore orbitale che portano ad una ripetizione periodica delle posizioni relative di
Sole, Giove e dell’asteroide. Ciò in quanto per certi valori del semiasse dell’orbita si
verifica una situazione in cui il periodo di rivoluzione corrispondente risulta essere
una frazione semplice del periodo di Giove. Ad esempio, l’importante lacuna di
Kirkwood a 2.5 UA corrisponde ad orbite caratterizzate da un periodo di rivoluzione
intorno al Sole pari ad un terzo esatto di quello di Giove. Una simile situazione fa sì
che l’eventuale asteroide risonante e Giove si ritrovino nella stessa posizione relativa
ogni tre rivoluzioni del pianetino, corrispondenti ad un anno gioviano. Ciò dà luogo
ad una cosiddetta risonanza di moto medio (v. fig. 8) e produce un potenziamento
dell’azione perturbatrice di Giove che finisce per espellere qualunque asteroide che
(ad esempio a causa di collisioni) vada e finire in quelle zone. Tali asteroidi vengono
in genere immessi su orbite di più basso periodo, diventando dei NEA.
Fig. 8 Diagramma schematico che spiega il meccanismo di risonanza di moto medio 1:3. Se
l'asteroide ed il pianeta sì trovano ad una data epoca nelle posizioni P e G1, l’asteroide si troverà di
nuovo in P dopo una rivoluzione completa. A quell’epoca, il pianeta si troverà in G2, mentre sarà in G3
dopo due rivoluzioni complete dell’asteroide. Al termine della terza rivoluzione dell’asteroide, viene
nuovamente a ripetersi la configurazione iniziale (da Cellino et al., 2000).
11
Dalla fig 7 si vede che le altre maggiori lacune di Kirkwood corrispondono a
risonanze del tipo 2/5, 3/8 e 4/9. Occorre tuttavia ricordare che non sempre le
situazioni di risonanza sono associate ad un meccanismo di espulsione dalla Fascia
Principale; talvolta, come nel caso delle risonanze del tipo n/(n+1), possono essere
associate ad un meccanismo di protezione. Ciò è quanto accade, ad esempio, per gli
oggetti Hilda e Thule, posti nelle risonanze 2/3 e 3/4, rispettivamente. In questi casi il
fatto che nella zona dove una risonanza si manifesta si abbia una lacuna oppure un
ammasso di asteroidi dipende dall’intervento di altre forze perturbative, diverse da
quella gravitazionale di Giove, come le forze gravitazionali di Saturno e degli altri
pianeti, le forze mareali del Sole e quelle dovute agli impatti con altri corpi minori. In
particolare Vrbik (1996) ha dimostrato che si ha una lacuna quando tali forze
perturbative addizionali riducono l’energia meccanica dell’asteroide, mentre, quando
al contrario tale energia viene aumentata, ciò comporta un’alta concentrazione di
corpi nella zona dove si ha la risonanza ed uno svuotamento delle regioni limitrofe.
Purtroppo, però, il discorso non si esaurisce qui, poiché nella realtà la
situazione è particolarmente complicata per la presenza di altre risonanze, diverse da
quelle di moto medio. Tra queste notevole rilievo assumono le cosiddette risonanze
secolari. In effetti, a causa delle perturbazioni planetarie, sia le orbite degli asteroidi
che quelle dei pianeti cambiano continuamente di orientazione nello spazio: si ha
contemporaneamente una precessione del piano orbitale (che nel caso della Terra dà
luogo al fenomeno della precessione degli equinozi) e una precessione del semiasse
maggiore dell’orbita (cioè una rotazione dell’orbita sul suo proprio piano) che dà
luogo al cosiddetto fenomeno dell’anticipo del perielio. Quando il periodo di uno di
questi due moti di precessione (tipicamente alcune decine di migliaia di anni) coincide
per un asteroide e per Giove (o Saturno), si ha appunto una risonanza secolare. Anche
questo tipo di risonanza è generalmente associato a fenomeni di comportamento
caotico su tempi scala molto brevi (Cellino et al., 2000). Pertanto, a causa di tutti
questi fattori tra loro strettamente interconnessi, in questa sede l’evoluzione dinamica
della fascia degli asteroidi non può che essere descritta in modo molto qualitativo.
6. Forme degli asteroidi
Nell’antichità gli unici corpi celesti di cui gli uomini potevano osservare la
forma erano il Sole e la Luna, che apparivano entrambi perfettamente rotondi (o
sferici, come ipotizzavano alcuni filosofi ed astronomi). Una forma geometrica così
regolare era ed è assai rara per la comune esperienza degli oggetti terrestri, che con
poche eccezioni (costituite da manufatti e prodotti dell’attività umana), normalmente
si presentano invece asimmetrici, scabri, spigolosi ed imperfetti. Anche questo
contrasto portò alla dicotomia, che dalla filosofia si estese al senso comune, fra la
supposta perfezione dei corpi celesti e la rozza materialità degli oggetti terrestri.
12
Oggi la situazione è molto cambiata. Quello che sappiamo è che esistono nel
Sistema Solare numerosi oggetti, come ad esempio gli asteroidi, di forma irregolare e
asimmetrica, simili per molti versi alle pietre o ai macigni della nostra esperienza
comune; d’altra parte sappiamo pure che esistono corpi, come il Sole, la Luna e i
pianeti, di forma sferica o comunque simmetrica, la qual cosa non impedisce però che
su piccola scala la superficie di questi oggetti sia, come quella terrestre, tutt’altro che
regolare e perfetta.
Consideriamo una pietra, un comunissimo pezzo di roccia che possiamo
trovare un po’ dovunque cercando per terra. Ci si potrebbe chiedere: come mai, in
linea di principio, è sempre possibile trovare corpi minori del Sistema Solare, che, a
parte i crateri, sono grosso modo una copia molto ingrandita della nostra pietra,
mentre non esistono pianeti di questa forma? Come mai, cioè, le forme irregolari sono
tanto comuni tra i corpi minori e non tra quelli di dimensioni planetarie? In termini
più precisi, come mai il rapporto tra le dimensioni delle irregolarità superficiali di un
corpo minore e quelle del corpo stesso può assumere valori dell’ordine dell’unità,
mentre per i pianeti tale rapporto non supera mai l’1% (ad esempio per la Terra questa
percentuale è dell’ordine dello 0.1%)?
La risposta è molto semplice. La forma di un corpo è in genere determinata da
due tipi di forze in qualche modo antagoniste: quelle gravitazionali che si esercitano
tra le varie parti del corpo (“autogravitazione”) e quelle di coesione (anche dette
“forze di stato solido”) che sono dovute alle interazioni elettromagnetiche fra le
molecole del corpo stesso. Le prime sono in grado di plasmare e compattare i corpi
abbastanza massicci da generare un’autogravità significativa; le seconde, che sono
quelle che tengono uniti gli oggetti solidi della nostra esperienza quotidiana, hanno
una geometria, già complessa a livello microscopico, che fa sì che in qualche modo i
corpi “abbiano memoria” delle deformazioni subite nel corso della loro storia. Pertanto
le forme regolari o simmetriche sono tipiche dei corpi massicci la cui struttura è
determinata principalmente dall’autogravitazione; al contrario, per i corpi con una
gravità troppo debole, le forze di stato solido contrastano efficacemente quella che
potremmo definire “la pialla gravitazionale” e fanno sì che i piccoli corpi possano
assumere forme irregolari e asimmetriche.
Evidentemente, come già osservato, su piccola scala anche le superfici dei
pianeti presentano irregolarità e rilievi, come catene montuose e crateri. In questi casi
tali irregolarità hanno però dimensioni trascurabili rispetto a quelle planetarie.
Quando invece le dimensioni delle irregolarità divengono confrontabili con quelle
dell’oggetto interessato, allora la forma regolare scompare e ciò che resta è di fatto un
macigno cosmico.
Per valutare a quale dimensione avviene la transizione appena descritta,
occorre ricordare che ogni corpo solido dotato di una certa rigidità resiste alle
13
deformazioni fino ad un certo limite critico oltre il quale il corpo si spezza.
Rifacendoci all’approccio seguito da Farinella (1982), possiamo considerare a titolo
d’esempio il comportamento di una sbarra. E’ facile rendersi conto che la grandezza
fisica che dà una misura di questo limite di rottura deve essere una forza (ossia la
forza esterna deformante che provoca la rottura) divisa per una superficie (la sezione
della sbarra); ciò in quanto la forza critica è proporzionale alla sezione della sbarra.
Abbiamo quindi a che fare con una pressione critica per la rottura, che dipende in
prima approssimazione solo dal tipo di materiale che costituisce il corpo. In generale
anche la forma del corpo determina la sua resistenza alla rottura, ma per forme non
troppo estreme la dipendenza dalla forma si può trascurare. La pressione critica S è
ovviamente incognita per i materiali costituenti i corpi celesti.
Cominciamo dal caso “regolare” e consideriamo la situazione limite in cui S è
nulla, cioè il materiale si comporta come un fluido che non oppone resistenza alle
deformazioni. Occorre subito precisare che questa situazione è molto meno
speculativa di quanto a prima vista si potrebbe ritenere, dal momento che esistono
fondati sospetti (come vedremo tra poco) che alcuni corpi minori del Sistema Solare
siano in realtà dei mucchi di massi tenuti insieme dalla mutua attrazione
gravitazionale. In tal caso la forma del corpo dipende da tre fattori:
a) la distribuzione della massa al suo interno; b) la velocità angolare di rotazione e c)
l’eventuale presenza di un altro corpo (primario) dotato di un campo gravitazionale
significativo; ciò accade ad esempio nel caso dei satelliti dei pianeti.
Escludiamo per il momento quest’ultimo fattore e limitiamo la discussione al
caso più semplice: quello in cui la densità non varia all’interno del corpo. In tal caso
la forma di equilibrio è una sfera se la velocità angolare è nulla, mentre, se 0,
le forme di equilibrio sono degli ellissoidi sempre più schiacciati lungo l’asse di
rotazione man mano che aumenta (a causa della forza centrifuga dovuta alla
rotazione assiale). Quando la forma diventa troppo allungata, l’ellissoide diventa
instabile ed il corpo si scinde in due o più pezzi.
Se poi il corpo è immerso nel campo gravitazionale di un oggetto massivo,
allora la forma è “distorta” non solo a causa della forza centrifuga, ma anche del fatto
che il primario attrae gravitazionalmente di più la parte del satellite ad esso più vicina
che non quella più lontana. Come avviene per quasi tutti i satelliti reali, si può
supporre che, per effetto delle forze mareali, i corpi in esame abbiano orbite quasi
circolari e compiano una rotazione sul proprio asse nello stesso tempo in cui
completano un giro intorno al pianeta. In queste ipotesi si può provare che più il
satellite ruota velocemente (cioè più è vicino al primario), più la sua forma si
allontana da una sfera, assumendo l’aspetto di un ellissoide triassiale con l’asse più
lungo costantemente puntato verso il pianeta. Ovviamente anche in questo caso,
quando la deformazione supera un certo limite, il corpo non può rimanere integro e
14
tende a spezzarsi: è questo il cosiddetto “limite di Roche” che è appunto la
conseguenza del fatto che un satellite “fluido” non può sopravvivere intatto troppo
vicino al suo primario.
Possiamo quindi concludere che, quando S = 0, il corpo assume sempre forme
più o meno simmetriche e regolari.
Forme irregolari sono invece possibili nel caso in cui il materiale è solido (S
0). Consideriamo infatti un’irregolarità, o se vogliamo una montagna, sulla superficie
di un corpo celeste. La montagna di altezza h eserciterà alla sua base una pressione:
P gh h
GM
R2
dove G è la costante gravitazionale, è la densità del materiale, mentre g, M ed R
sono rispettivamente l’accelerazione di gravità, la massa ed il raggio del corpo in
esame.
Evidentemente la montagna verrà schiacciata sotto il proprio peso se la sua altezza h
supera un valore massimo hmax tale che che Pmax = S, ossia:
hmax
S R2
3S
GM
4 G 2 R
.
(1)
Si può definire come “regolare” la forma di un corpo celeste per cui hmax/R < 0.1, cioè
per il quale i più alti rilievi non superano il 10% del raggio (ad esempio per la Terra
questa percentuale è dell’ordine dello 0.1%). Questa definizione è anche
intuitivamente ragionevole poiché in genere un corpo per cui hmax/R > 0.1 avrà tali
gibbosità e/o avvallamenti da perdere ogni apparenza di regolarità. Accoppiando
questa definizione con la (1), otteniamo che il raggio critico al di sopra del quale
possiamo aspettarci di trovare corpi di forma regolare sarà:
Rc
15 S
.
2 G 2
Il raggio critico dipende quindi dalla densità e dalla resistenza alla rottura del
materiale costituente il corpo. Se prendiamo come casi tipici il ghiaccio ( = 1 g cm-3,
S 106 dine cm-2) e le rocce terrestri ( = 3 g cm-3, S 109 dine cm-2), si ottiene
rispettivamente Rc 60 km ed Rc 600 km. Per un materiale di tipo meteoritico con
= 2 g cm-3 ed S 107 dine cm-2 risulta invece Rc 100 km.
Questi risultati indicano che un corpo con diametro maggiore o comunque
prossimo a 1000 km ha sicuramente una forma regolare, indipendentemente dal
materiale che lo costituisce. E ciò risulta in perfetto accordo con le osservazioni che
mostrano appunto che tutti i corpi più grandi del Sistema Solare (pianeti, grandi
15
asteroidi, come Vesta e Pallade, e i maggiori satelliti, come ad esempio la Luna,
Titano, Tritone ed i satelliti galileiani di Giove) hanno forme regolari.
La transizione a forme irregolari deve necessariamente avvenire per
dimensioni pari a quelle tipiche degli asteroidi e dei satelliti minori. In particolare
quello che ci aspettiamo sulla base del semplice modello sopra esposto è che nel caso
degli asteroidi caratterizzati da = 2 g cm-3 ed S 107 dine cm-2, corpi con
dimensione D > 200 km devono avere forme regolari, mentre quelli con D < 200 km
devono essere irregolari. In effetti ciò è in sostanziale accordo con quanto indicato
dalle poche osservazioni dirette effettuate dalle sonde spaziali Galileo e NEAR (Ida,
Gaspra, Matilde ed Eros, tutti irregolari, hanno dimensioni minori di 60 km) e
dall’analisi delle curve di luce di un cospicuo numero di asteroidi. Tali osservazioni
indirette permettono di valutare sia il periodo che l’entità delle deviazioni dalla
simmetria rispetto all’asse di rotazione (attraverso la misura dell’ampiezza della
curva). Ebbene, ciò che si osserva è che la forma degli asteroidi di dimensioni
inferiori a 100 km è irregolare (Farinella, 1982), il che indica una chiara prevalenza
delle forze di stato solido. Al contrario, i pochi asteroidi con diametro maggiore di
300 km hanno forme regolari con deviazioni massime di qualche percento (Farinella,
1982). Si ritiene pertanto che l’autogravità sia determinante per la loro forma e
struttura: le frequenti collisioni con altri asteroidi grandi fino ad 1/10 delle dimensioni
dell’oggetto bersaglio hanno probabilmente frammentato almeno gli strati superficiali
senza tuttavia poter distruggere l’asteroide. Infine, quello che si osserva nel dominio
intermedio (100 km D 300 km) è la presenza di una certa quantità di rotatori
mediolenti con forme regolari e simmetriche (Farinella, 1982). Tale osservazione non
solo non sorprende, a causa del fatto che il diametro critico di 200 km è esattamente al
centro dell’intervallo, ma è anche quello che esattamente ci si aspetta sulla base della
seguente considerazione. Sebbene la rottura collisionale di oggetti di questa taglia sia
abbastanza probabile, la loro autogravità è abbastanza intensa da far sì che, dopo la
rottura, molti frammenti non abbiano velocità sufficienti ad allontanarsi
indefinitamente ma ad un certo punto debbano invertire il loro moto, “ricadendo” gli
uni sugli altri: i prodotti finali del processo sono stati chiamati “mucchi di pietre”
(“rubble pile”), cioè ammassi di materiale più o meno finemente frammentato e di
pezzi più grossi tenuti insieme soltanto dalla reciproca attrazione gravitazionale. Tali
blocchi principali potrebbero essere separati l’uno dall’altro all’interno della struttura
oppure potrebbero essere a contatto reciproco, dando origine ad un aggregato
relativamente compatto; anche in questo caso, però, i numerosi spazi vuoti tra i
blocchi abbasserebbero notevolmente la densità dell’aggregato. Dal momento che per
questi strani oggetti la resistenza alle deformazioni è evidentemente molto ridotta,
dovremo aspettarci delle forme regolari non troppo dissimili da quelle che si
ottengono per i corpi con S = 0 (v. sopra), il che è appunto quello che si osserva. In
16
qualche caso ci si trova addirittura di fronte ad asteroidi doppi, come nel caso del
sistema IdaDattilo, fotografato dalla sonda Galileo (v. fig. 9), nonché Calliope e
Linus, Eugenia e Petit Prince, Ermione A e B, Antiope A e B, osservati dalla Terra.
Fig. 9 Foto ripresa dalla sonda Galileo che mostra l’asteroide Ida (a sinistra) ed il suo satellite
naturale Dattilo (a destra). Ida è un asteroide altamente craterizzato e dalla forma irregolare che orbita
nella Fascia Principale. Esso ha una dimensione di 56 km. Dattilo appare più piccolo non per un effetto
prospettico ma a causa delle sue dimensioni veramente ridotte (pari a circa 1.5 km). I ricercatori del
team della missione Galileo hanno valutato che Dattilo è distante grosso modo 100 km dal centro di Ida
(dal sito web http:// solarsystem.nasa.gov/.multimedia/ gallery/ ).
17
APPENDICI
Appendice A
Determinazione del raggio e dell’albedo di un corpo tramite misure di flusso nel
visibile e nel FIR
Il flusso osservato sulla Terra della radiazione solare riflessa dal corpo nel
visibile è:
2
V
R
F
R
AV FSV r
(A1)
con ed FSV(r) (rispettivamente distanza Terra-asteroide e flusso solare nel visibile
alla distanza orbitale r dell’asteroide) noti, FRV misurato, e con R (raggio
dell’asteroide) e AV (albedo nel visibile) da determinare.
Il flusso emesso dal corpo osservato a Terra nel FIR vale:
2
FIR
E
F
2
R
R
FIR BFIR T BFIR T
(A2)
con FEFIR misurato, FIR (emissività del corpo nel lontano infrarosso) assunta uguale
all’unità e T (temperatura dell’asteroide) data da:
2
T
4
R
(1 AV ) S TS
r
(A3)
con RS e TS (raggio e temperatura solare) noti.
Si hanno tre equazioni nelle incognite AV, R e T. Si assume un valore di prova
per AV, ricavando R dalla (A1) e T dalla (A3). Tali valori si sostituiscono nella (A2) e,
per approssimazioni successive si ricavano i valori corretti delle tre incognite.
18
Appendice B
Classi tassonomiche asteroidali
class
mean
albedo
spectral reflectivity (0.3-1.1 micrometres)
C
0.05
neutral, slight absorption at wavelengths of
0.4 micrometre or shorter
D
0.04
very red at wavelengths of 0.7 micrometre or
longer
F
0.05
flat
P
0.04
featureless, sloping up into red*
G
0.09
similar to C class but with a deeper
absorption at wavelengths of 0.4
micrometre or shorter
K
0.12
similar to S class but with lower slopes
T
0.08
moderately sloped with weak ultraviolet and
infrared absorption bands
B
0.14
similar to C class but with shallower slope
toward longer wavelengths
M
0.14
featureless, sloping up into red*
Q
0.21
strong absorption features shortward and
longward of 0.7 micrometre
S
0.18
very red at wavelengths of less than 0.7
micrometre, typically with an absorption band
between 0.9 and 1.0 micrometre
A
0.42
extremely red at wavelengths shorter than 0.7
micrometre and a deep absorption longward of
0.7 micrometre
E
0.44
featureless, sloping up into red*
R
0.35
similar to A class but with slightly weaker
absorption bands
V
0.34
very red at wavelengths of less than 0.7
micrometre and a deep absorption and centred
near 0.95 micrometre
Other
classes
any
any object not falling into one of the above
NOTES
(*): Classes E, M, and P are spectrally indistinguishable at these
wavelengths and require an independent albedo measurement for
unambiguous classification.
19
Bibliografia
Chapman, C.R.: 1975, Le Scienze, 81, 26.
Cellino, A., et al.: 2000, Il rischio asteroidi, Settore Protezione Civile, Regione Piemonte.
Farinella, P.: 1982, Giorn. di Astr., 8, 349.
Gribbin, J.: 2004, Astronomia (Garzanti Libri S.p.A., Milano).
Herrmann, J.: 1978, Atlante di astronomia (Mondadori, Milano).
Jessberger, E.K.: 1981, Meteors and Meteorites , in Landolt-Börnstein, Gruppe G, Band 2a, Shaiffers
Hsg. K., and Voigt H.H. eds., Spinger-Verlag, Heidelberg, p. 187.
Jessberger, E.K.: 1991, in Solid State Astrophysics, Bussoletti E., Strazzulla, G.. eds., North – Holland,
Amsterdam, p. 107 .
Mukai, T.: 1989, in Evolution of Interstellar Dust and Related Topics, Bonetti A., Grenberg J.M.,
Aiello S. eds., North – Holland, Amsterdam, p.397.
Rabinowitz, D.., et al.: 2000, Nature, 403, 165 .
Sandford , S.A.: 1989, in Interstellar Dust, Allamandola L.J. and Tielens A.G.G.M. eds, p. 403.
Sandford, S.A., Walker, R.M.: 1985, Astrophys Jou., 291, 838.
Whipple, F.L.: 1967, in The Zodiacal Light and the Interplanetary Medium, Weinberg J. ed., NASA
SP-150, p. 409.
20