albero binario di ricerca
• albero binario che soddisfa la
seguente proprietà
Algoritmi e strutture dati
per ogni nodo, tutte le chiavi nel
suo sottoalbero sinistro sono !
della chiave v associata al nodo e
tutti le chiavi nel suo sottoalbero
destro sono " di v
•Alberi binari di ricerca (BST)
Algoritmi e strutture dati
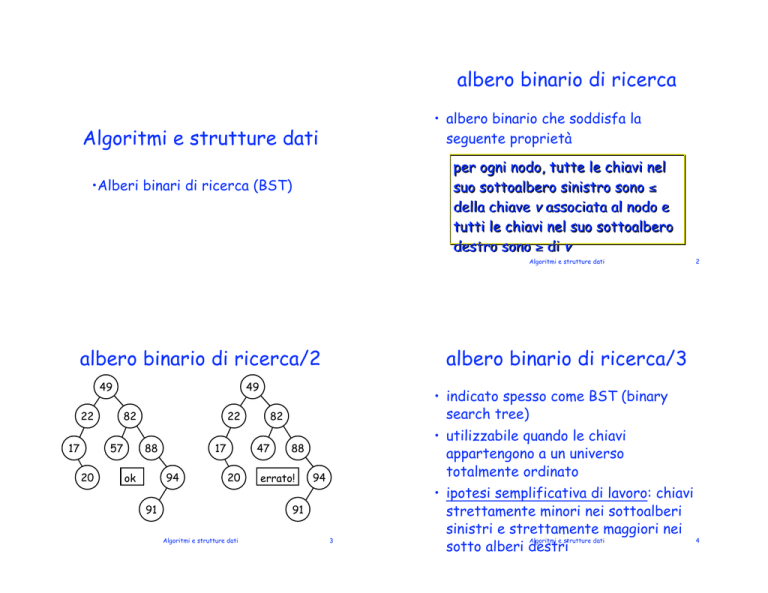
albero binario di ricerca/2
49
22
17
57
20
albero binario di ricerca/3
49
82
22
88
17
94
ok
20
91
• indicato spesso come BST (binary
search tree)
82
47
• utilizzabile quando le chiavi
appartengono a un universo
totalmente ordinato
88
errato!
94
91
Algoritmi e strutture dati
2
3
• ipotesi semplificativa di lavoro: chiavi
strettamente minori nei sottoalberi
sinistri e strettamente maggiori nei
Algoritmi e strutture dati
4
sotto alberi destri
rappresentazione
collegata dei nodi
rappresentazione dei nodi
public class BSTNode {
/* Qui può essere presente un campo info */
protected Comparable key;
• in molti casi può essere la stessa
usata negli alberi binari (classe
BinaryNode)
// interface Comparable richiede metodo compareTo
BSTNode left, right; // rappr. minima
public BSTNode() {…}
public BSTNode(Object el) {…}
public BSTNode(Object el, BSTNode lt, BSTNode rt) {…}
public void visit() { key.visit(); }
public boolean isLeaf() {…}
– in alternativa, la si può estendere
• per le variabili membro possiamo
usare lo specificatore di accesso
private o protected
– le conseguenze sono differenti
Algoritmi e strutture dati
}
5
public interface Comparable
6
public interface Comparable/2
• public int compareTo(Object o)
• returns a negative integer, zero, or a positive integer as
this object is less than, equal to, or greater than the
specified Object o
– The implementor must ensure sgn(x.compareTo(y)) == sgn(y.compareTo(x)) for all x and y. (This implies that
x.compareTo(y) must throw an exception iff y.compareTo(x) throws
an exception.)
– The implementor must also ensure that the relation is transitive:
(x.compareTo(y)>0 && y.compareTo(z)>0) implies x.compareTo(z)>0
– Finally, the implementer must ensure that x.compareTo(y)==0
implies that sgn(x.compareTo(z)) == sgn(y.compareTo(z)), for all z
Algoritmi e strutture dati
Algoritmi e strutture dati
7
• It is strongly recommended, but not strictly
required that (x.compareTo(y)==0) ==
(x.equals(y)). Generally speaking, any class
that implements the Comparable interface
and violates this condition should clearly
indicate this fact. The recommended
language is "Note: this class has a natural
ordering that is inconsistent with equals"
Algoritmi e strutture dati
8
operazioni sui BST
altre operazioni sui BST
public interface BST {
void clear();
boolean isEmpty();
BSTNode search(BSTNode p, Comparable el);
void insert(BSTNode node);
boolean isInTree(Comparable el);
int getSize();
void inorder(BSTNode p);
void preorder(BSTNode p);
void postorder(BSTNode p);
void breadthFirst();
int treeHeight(BSTNode radice);
void delete(Comparable el);
}
Algoritmi e strutture dati
BSTNode minimum(BSTNode v);
BSTNode maximum(BSTNode v);
BSTNode successor(BSTNode v);
BSTNode predecessor(BSTNode v);
D.: quali sono gli elementi max. e min. ?
9
elementi o nodi?
Algoritmi e strutture dati
10
ricerca in un BST
• il metodo che implementa l’operazione
search può restituire elementi (Object) o
nodi (BSTNode)
BSTNode search(BSTNode p, Comparable el) {
while (p != null)
if (el.equals(p.key))
return p;
else if (el.compareTo(p.key)<0)
p = p.left;
else p = p.right;
return null; /* Se non lo trova */
}
– Object
• viene rafforzato l’incapsulamento
• variabili membro protected
– BSTNode
• operazioni su sottoalberi
• variabili membro private e metodi
accessori/modificatori
• il dilemma vale anche per altri metodi
– successor, delete
(parametro
Algoritmi
e strutture dati formale), …
11
Algoritmi e strutture dati
12
Versione ricorsiva
costo della ricerca in un BST
BSTNode search(BSTNode p, Comparable el) {
if(p == null)
return null;
if (el.compareTo(p.key)<0)
return search(p.left, el);
else
if (el.compareTo(p.key)>0)
return search(p.right,el);
else return p;/* Trovato !! */
}
Algoritmi e strutture dati
BST di n nodi
21 52
• caso peggiore
56
54 67
– O(n)
77
• caso medio
– dipende dalla distribuzione
75
83
• caso migliore
13
costo della ricerca in un BST/2
• nel caso di distribuzione uniforme
delle chiavi il valore atteso
dell'altezza dell'albero è O(lg n)
– O(1) (poco interessante)
Algoritmi e strutture dati
14
analisi del caso medio
• IPL (internal path length):
somma lungh. percorsi radice-nodo,
per tutti i nodi
– N.B. L'altezza di un albero binario di n
nodi varia in {#lg2 n$ + 1,…, n}
° un BST con chiavi uniformemente
distribuite ha un costo atteso di
ricerca O(lg Algoritmi
n) e strutture dati
49
• lungh. media percorso radice-nodo:
IPL/(#nodi)
15
Algoritmi e strutture dati
16
analisi del caso medio/2
• chiavi 1,…,n presenti in un BST di n nodi (senza
perdita di generalità)
nuovo nodo u viene inserito come foglia
• Pn (i ): percorso medio in BST di n nodi avente
chiave i in radice
• Pn : percorso medio in BST di n nodi
se k(radice) = i
allora
– sottoalbero sx ha
i – 1 chiavi
– sottoalbero dx ha
n – i chiavi
inserimento in un BST
(Pi !1 + 1)(i ! 1) + (Pn !i + 1)(n ! i )
n
n
" Pn (i ) = ... = O(lg n )
Pn = i =1
n
• fase 1: cerca il nodo genitore v
Pn (i ) =
Algoritmi e strutture dati
17
inserimento in un BST/2
public void insert(Comparable el) {
BSTNode p = root, prev = null;
while (p != null) {
prev = p;
if (p.key.compareTo(el)<0)
p = p.right;
else p = p.left;
}
if (root == null) // albero vuoto;
root = new BSTNode(el);
else if (prev.key.compareTo(el)<0)
prev.right = new BSTNode(el);
else prev.left = new BSTNode(el);
}
Algoritmi e strutture dati
• fase 2: inserisci u come figlio di v
Algoritmi e strutture dati
18
inserimento in un BST/3
fase 1
fase 2
19
• la fase 1 termina quando
si raggiunge un nodo del
BST privo del figlio in
cui avrebbe avuto senso
continuare la ricerca
– non necessariamente una
foglia
• la fase 2 si limita a
collegare una nuova
Algoritmi e strutture dati
foglia
60
49
21 52
56
54 67
77
75
83
20
costo dell'inserimento
in un BST
inserimento in un BST/4
caso peggiore
• costo fase 1: O(n )
• costo fase 2: O(1)
• costo totale: O(n )
caso medio (distrib. unif.)
• costo fase 1: O(lg n )
• ogni inserimento introduce una nuova
foglia
49
21 52
• il costo è (proporzionale a) la
lunghezza del ramo radice-foglia
56
54 67
60 77
75
• nel caso peggiore O(n )
83
• costo fase 2: O(1)
Algoritmi
• costo totale: O(lg
ne)strutture dati
21
cancellazione da un BST
22
cancellazione da un BST/2
cancellazione di una foglia
tre casi
1.
Algoritmi e strutture dati
• basta individuare il nodo genitore e
mettere a null la variabile membro
opportuna (left o right)
cancellazione di una foglia
2. cancellazione di un nodo con un solo figlio
3. cancellazione di un nodo con due figli
Algoritmi e strutture dati
23
• individuare il genitore significa
sostanzialmente effettuare una ricerca
(come nella fase 1 dell'inserimento)
– un approccio alternativo è basato sulla
tramatura dell'albero (i nodi contengono altri
e strutture
dati
riferimenti, adAlgoritmi
es., al
genitore)
24
cancellazione da un BST/3
cancellazione da un BST/4
cancellazione di un nodo u con un solo figlio v
cancellazione di 83
• individuare genitore w di u
49
49
49
21 52
21 52
21 52
– se u è radice v diviene la nuova radice
56
56
56
54 67
54 67
54 67
60 77
60 77
60 77
75
75
75
83
83
Algoritmi e strutture dati
• se esiste w, sostituire al collegamento
(w,u ) il collegamento (w,v ) w
v
25
cancellazione da un BST/4
49
49
21 52
21 52
21 56
54 67
54 67
60 77
75
75
Algoritmi e strutture dati
u
v
u
v
u
Algoritmi e strutture dati
26
• individuare predecessore v (o successore)
di u (secondo il valore della chiave)
54 67
60 77
v
cancellazione di un nodo u con due figli (ci si
riconduce ad uno dei casi precedenti –
cancellazione per copiatura)
49
56
u
w
cancellazione da un BST/5
cancellazione di 52
56
w
w
– v non può avere due figli, altrimenti non sarebbe
predecessore (successore)
60 77
75
• copiare la chiave di v al posto di quella di u
27
• cancellare nodo v
Algoritmi e strutture dati
– v è foglia o ha un solo figlio
28
Cancellazione per copiatura/2
cancellazione per copiatura
u
v
v
v
w
lla
ce
w
v
w
can
w
u
u
copia chiave
u
public void deleteByCopying(Comparable el) {
BSTNode node, p = root, prev = null;
while (p != null && !p.key.equals(el)) {
prev = p;
if (p.key.compareTo(el)<0)
p = p.right;
else p = p.left;
}
node = p;
/* Cerca il nodo */
/* Continua alla prossima slide ..... */
Algoritmi e strutture dati
29
Cancellazione per copiatura/3
/* Dalla slide precedente .... */
30
Cancellazione per copiatura/4
/* Dalla slide precedente .... */
if (p != null && p.key.equals(el)) {
if (node.right == null)
node = node.left;
else if (node.left == null)
node = node.right;
/* Casi semplici: il nodo ha un solo figlio */
/* Continua .... */
Algoritmi e strutture dati
Algoritmi e strutture dati
31
else { /* Due figli .... */
BSTNode tmp = node.left;
BSTNode previous = node;
while (tmp.right != null) {
previous = tmp;
tmp = tmp.right;
}
node.key = tmp.key;
/* Copia anche info se presente */
if (previous == node)
previous.left = tmp.left;
else previous.right = tmp.left;
} /* Continua ... */
Algoritmi e strutture dati
32
Cancellazione per copiatura/5
/* Dalla slide precedente .... */
• la cancellazione di un
nodo interno richiede
l'individuazione del nodo
da cancellare nonché del
suo predecessore (o
successore)
if (p == root) /* Trova padre nuovo nodo */
root = node;
else if (prev.left == p)
prev.left = node;
else prev.right = node;
}
else if (root != null)
System.out.println(“Elemento assente”);
else System.out.println(“Albero vuoto");
Algoritmi e strutture dati
33
Cancellazione per fusione
v
n/2
34
• Cosa produce la visita simmetrica se
le chiavi sono stringhe?
x
w
x
Algoritmi e strutture dati
u
• Si implementi il metodo di visita in
ordine simmetrico
v
w
n/2
Domande
u: nodo da cancellare
x: nodo predecessore di u
v
da cancellare
• nel caso peggiore
entrambi i costi sono
predecessore
lineari: O(n ) + O(n ) =
Algoritmi e strutture dati
O(n )
}
u
costo della cancellazione
in un BST
35
• Perché per implementare le basi di
dati si usano alberi e non array?
Algoritmi e strutture dati
36












