Cap.4
Cap. 4: Forze e Momenti
Forza
Il concetto di forza serve ad esprimere l’interazione tra corpi. Quando si spinge o si tira un
oggetto, si interagisce con esso esercitando una forza e conseguentemente modificandone lo stato di
quiete o di moto. Per esperienza crediamo che certi tipi di forza richiedono un contatto tra i corpi:
ad esempio, quando calciamo un pallone ci sembra di esercitare una forza toccando la palla col
piede. Invece altre forze agiscono chiaramente senza un contatto diretto, come la forza repulsiva di
due magneti, o l’attrazione gravitazionale tra Sole e pianeti. Spesso le forze del primo tipo sono
dette forze di contatto. Ma in realtà la distinzione tra forze di contatto e non di contatto è solo
apparente. Per quanto compatto possa apparire un corpo, i suoi atomi sono tenuti separati e in
posizione da interazioni a distanza, come accade per i pianeti che ruotano attorno ad una stella.
Quando si calcia un pallone, a livello microscopico non c’è un contatto diretto tra gli atomi della
palla e del piede, ma un’interazione a distanza. In questo caso però la distanza è così piccola che i
nostri sensi non la percepiscono.
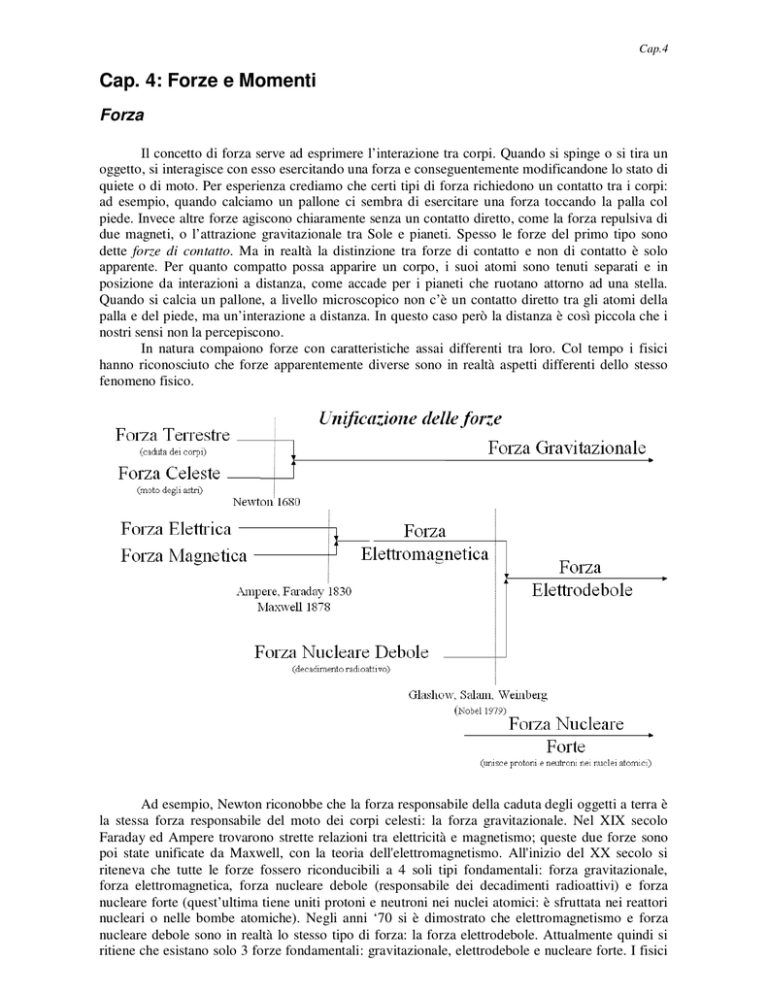
In natura compaiono forze con caratteristiche assai differenti tra loro. Col tempo i fisici
hanno riconosciuto che forze apparentemente diverse sono in realtà aspetti differenti dello stesso
fenomeno fisico.
Ad esempio, Newton riconobbe che la forza responsabile della caduta degli oggetti a terra è
la stessa forza responsabile del moto dei corpi celesti: la forza gravitazionale. Nel XIX secolo
Faraday ed Ampere trovarono strette relazioni tra elettricità e magnetismo; queste due forze sono
poi state unificate da Maxwell, con la teoria dell'elettromagnetismo. All'inizio del XX secolo si
riteneva che tutte le forze fossero riconducibili a 4 soli tipi fondamentali: forza gravitazionale,
forza elettromagnetica, forza nucleare debole (responsabile dei decadimenti radioattivi) e forza
nucleare forte (quest’ultima tiene uniti protoni e neutroni nei nuclei atomici: è sfruttata nei reattori
nucleari o nelle bombe atomiche). Negli anni ‘70 si è dimostrato che elettromagnetismo e forza
nucleare debole sono in realtà lo stesso tipo di forza: la forza elettrodebole. Attualmente quindi si
ritiene che esistano solo 3 forze fondamentali: gravitazionale, elettrodebole e nucleare forte. I fisici
Cap.4
teorici stanno elaborando nuove teorie per completare l’unificazione delle forze. Il cosiddetto
Modello Standard, in fase di validazione grazie anche agli esperimenti con la nuova macchina
acceleratrice del CERN di Ginevra, è una teoria che descriverebbe in modo unitario Forza
Elettrodebole e Nucleare Forte.
Seppure esistano solo 3 forze fondamentali, per motivi pratici si usano nomi e trattazioni
teoriche particolari per la forza elettrodebole a seconda del contesto. Si parlerà quindi ora di “spinta
di Archimede”, ora di “forze di attrito”, ora di “reazioni vincolari”, ecc. Infatti l’enorme numero di
molecole presenti nei corpi macroscopici rende impensabile applicare la teoria della forza
elettrodebole direttamente alle singole molecole per risolvere problemi pratici. In questi casi si
useranno invece semplici leggi semiempiriche (si veda ad esempio il paragrafo sulle forze di
attrito).
Nel sistema MKS le forze si esprimono in Newton, [N], o [kg][m][s]-2. Il Newton ha le dimensioni
di una massa per un’accelerazione. Anche il peso è una forza: è il prodotto tra la massa m del corpo
e l’accelerazione di gravità g: P=mg.
La forza peso può servire da campione per misurare le forze. Lo strumento
di misura è il dinamometro a molla. Si misura il peso di un campione di
riferimento col dinamometro, osservando l'allungamento della molla. Tutte
le altre forze possono essere misurate applicandole alla molla del
dinamometro, e misurando l'allungamento della molla in rapporto
all'allungamento del campione standard.
L’esperienza indica che le forze sono caratterizzata da una intensità, da una
direzione, da un verso e da un punto di applicazione. Per questo motivo è
assai utile rappresentare le forze con vettori. Questo consentirà di sommare
più forze applicate sullo stesso corpo utilizzando l’algebra vettoriale.
Esempio: somma di più forze applicate ad un punto con
l’algebra vettoriale.
F2
F1
Due uomini stanno tirando ognuno una corda legata ad un
anello. L’anello regge un peso di 300 N. I due uomini tirano
le corde con forza F1 ed F2, entrambe di modulo pari a 200 N.
Le corde formano un angolo di 45° con la verticale.
P
Trovare la forza risultante R, somma di tutte le forze che
agiscono sull’anello.
Fig.1
Cap.4
Sull’anello agiscono 3 forze: F1 ed F2 esercitate dalle corde, ed il peso P: Le espressioni analitiche
dei 3 vettori sono:
F1x
F2 x
Px
F1= ; F2= ; P= ;
F1 y
F2 y
Py
Il vettore risultante è R = F1+ F2+P
Le componenti orizzontale e verticale delle forze sono:
F1x=200cos45°=200x0.707=141.4 N
F2x= -F1x=-141.4 N
F1y=200sen45°=200x0.707=141.4 N
F2y= F1y= 141.4 N
Px=0
Py=-300 N
Sommando separatamente le componenti orizzontali e verticali otteniamo le componenti di R:
F1x F2 x Px 141.4 − 141.4 + 0 0
R= + + =
=
F1 y F2 y Py 141.4 + 141.4 − 300 − 17.2
Esempio: somma di più forze applicate ad un punto col metodo grafico. Il calcolo della forza
risultante R esercitata dal muscolo gastrocnemio come somma delle componenti prodotte dal
gemello mediale e dal gemello laterale è risolto graficamente (regola del parallelogramma) nel
disegno seguente.
Cap.4
Momento di una forza
L’esperienza indica che la capacità che ha una forza applicata ad un corpo di produrre una
rotazione del corpo cambia a seconda del punto di applicazione della forza. E’ per questo motivo
che la maniglia delle porte è sempre messa nel punto orizzontalmente più distante rispetto ai
cardini. Infatti, se la maniglia fosse messa vicino ai cardini, faremmo più fatica ad aprire la porta,
anche se peso e attriti della porta non cambiano. Similmente, svitiamo un dado con minor fatica se
impugniamo una chiave inglese all’estremità opposta al dado piuttosto che vicino al dado.
Per cui la capacità di una forza di esercitare una rotazione dipende dal punto di applicazione
della forza. Per esprimere questo concetto in fisica si è introdotta un’altra grandezza vettoriale: il
momento di una forza.
Il momento M di una forza F rispetto ad un punto P è un vettore, definito come prodotto
vettoriale b × F. Se b il vettore che congiunge il punto P col punto di applicazione della forza
(questo vettore è detto braccio) allora la direzione del vettore momento M è perpendicolare al piano
dove si trovano F e b . In questo corso considereremo solo problemi “a due dimensioni”, dove b ed
F possono essere disegnati sul foglio. Allora il vettore momento “uscirà” perpendicolarmente dal
foglio.
Volendo esprimere M in forma analitica, dobbiamo allora considerare che in genere questo
vettore avrà tre componenti: nella direzione x, Mx, nella direzione y, My, e nella direzione z, Mz:
M x
M= M y
M z
Nel caso in cui i vettori b ed F giacciano nel piano X-Y del foglio, allora la sola componente
Mz sarà diversa da zero
0
M= 0
M z
Se braccio b e la forza F sono tra loro perpendicolari, allora il modulo del momento |M| è
semplicemente dato dal prodotto braccio × forza: |M|= |b |×|F|. Se invece braccio e forza formano tra
loro un angolo qualsiasi, il momento è dato dal prodotto tra il braccio e la sola componente della
forza perpendicolare al braccio. Se ϑ è l’angolo tra b ed F, allora la componente di F
perpendicolare a b è |F| sen(ϑ ) e quindi:
|M|=|b | |F| sen(ϑ )
Cap.4
P
ϑ
b
F
Fig.2
Se ad esempio F è applicata con angolazione ϑ ad un’asta lunga b incernierata in P come indicato in
fig.2, allora il momento M è un vettore diretto perpendicolarmente al foglio verso l’alto (regola
della mano destra), cioè con Mz>0, e di modulo pari a |b| |F| sen(ϑ). Notare che se la forza fosse
stata parallela al braccio b, ϑ=0, sen (0)=0 ed il momento sarebbe stato nullo.
Le dimensioni del momento M sono [m][N] o [Kg][m] 2 [s]-2.
Per la “regola della mano destra” è positivo il momento che produce una rotazione antioraria,
negativo quello che produce una rotazione oraria.
M<0
M>0
Esempio. Per aprire una porta larga 80 cm applichiamo una forza di 5 [N] tirando la maniglia.
Che momento esercitiamo rispetto ai cardini?
Lo schema è quello del disegno in figura. Poiché la maniglia si trova all’estremità della porta
opposta ai cardini, |r|=0.8 m. La forza è applicata perpendicolarmente alla porta, per cui ϑ=90°. Dal
momento che la rotazione sarà in senso orario, il momento è negativo. Per cui abbiamo: M=0.8x5xsen90°=-4 [m][N]
Cap.4
Esempio.
Un’insegna pesa 50 N.
E’ appesa ad un’asta che sporge da una
parete. L’asta è lunga 1 m.
L’angolo tra parete ed asta è di 60°.
Calcolare il momento prodotto dal peso
dell’insegna rispetto al punto in cui l’asta è
infissa nel muro.
Schematizziamo il problema indicando con “P” il punto del muro in cui l’asta è infissa, con W il
vettore peso:
P
60°
W
Anche l’angolo tra l’asta ed il peso è 60°.
Quindi la componente del peso perpendicolare all’asta è 50sin(60°).
La torsione generata è in senso orario e quindi il momento risultante è negativo.
= -1 [m]x 50 sin(60°) [N]
Mz
= -50x0.866
= -43.3 [Nm]
Quiz
La figura mostra una porta vista dall’alto. “A” è il cardine, “C” la maniglia e “B” il centro della porta.
A
B
C
A turno, quattro persone applicano le forze indicate qui sotto per aprire la porta.
A
B
C
F1
F2
F3
F4
La persona 1 spinge in “B” applicando la forza F1; la persona 2 tira la maniglia “C” perpendicolarmente
alla porta, con forza F2; 3 e 4 tirano la maniglia applicando le forze F3 ed F4 con l’inclinazione indicata.
Come si vede dal disegno, |F1|=|F2|<|F3 |<|F4|. Senza eseguire calcoli indicate:
1)Quale persona esercita il momento maggiore (in modulo) rispetto al cardine A;
2)Quale forza esercita il momento maggiore (in modulo) rispetto alla maniglia C
Cap.4
Quiz
Quali sono i momenti rispetto a polso, gomito e spalla di un peso di 20 N sul palmo di una mano:
a) di una persona col braccio disteso orizzontalmente?
b) di una persona col braccio che forma un angolo di 30° rispetto al corpo?
Cap.4
Momento di una coppia di forze.
Due forze uguali ed opposte le cui direzioni non siano allineate su una retta formano una coppia. La
forza risultante dalla somma delle forze della coppia è nulla. Però anche se non esercita una forza
risultante, ognuna delle due forze esercita un momento. Poiché la somma dei due momenti non si
annulla, la coppia esercita un momento risultante che tende a far ruotare il corpo.
Si dimostra che il momento risultante di una coppia di forze, M, non dipende dal punto P rispetto al
quale esso è calcolato, ma dipende solo dalla distanza tra i punti di applicazione delle due forze.
F
P
d
b
-F
Consideriamo ad esempio la coppia di forze -F e F della figura: la distanza tra P e la prima forza è
d; la distanza tra le due forze è b. Calcoliamo i momenti rispetto al punto P.
Mz=-d ×|F| + (d+b)×|F|= b×|F|
Quindi il modulo del momento di una coppia dipende solo dall’intensità delle due forze, |F|, e dalla
distanza tra loro, b.
Curva della coppia esercitata sulla trasmissione dal motore della motocicletta BMW K 1200 R
2005, al variare del numero di giri del motore.
Cap.4
Esempio: Porte Girevoli
Una persona sta entrando in albergo per una porta girevole, mentre
un’altra ne sta uscendo. Entrambe spingono sulla porta applicando
una forza di 50 [N].
Le forze applicate sono rappresentate nella figura seguente per due possibili casi:
Nel caso rappresentato a sinistra, le due forze formano una coppia con Mz<0: la porta girerà in senso
orario.
Nel caso di destra, il braccio della coppia è nullo (b=0) ed il momento risultante dalla somma dei
momenti delle due forze sarà Mz=0.












