INFINITA’ DEI NUMERI
PRIMI PALINDROMI DECIMALI
Gruppo Riemann*
Nardelli Michele, Francesco Di Noto
*Gruppo amatoriale per la ricerca matematica sui numeri primi, sulle loro congetture e sulle
loro connessioni con le teorie di stringa.
Abstract
In this paper we show our proof on the infinity palindrome
prime numbers
Riassunto
In questo lavoro cercheremo di dimostrare l’infinità dei
numeri primi palindromi, problema ancora irrisolto della
matematica
Quello dell’infinità o meno dei numeri primi palindromi in base
10, così come lo riporta Wikipedia alla voce “Problemi irrisolti in
1
Matematica”
•
“Dimostrazione dell'infinità dei primi palindromi in base 10” ,
è un altro dei problemi ancora irrisolti in matematica
Prima di affrontare l’argomento, riportiamo la voce “Numeri primi
palindromi”
Primo palindromo
Da Wikipedia, l'enciclopedia libera.
Un primo palindromo è un numero primo che è anche un numero palindromo, ossia rimane
invariato leggendolo da destra a sinistra. La palindromicità dipende dalla base del sistema di
numerazione, a differenza della primalità che è indipendente dalla base. I più piccoli primi
palindromi in base 10 sono (sequenza A002385 dell'OEIS):
2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301,
10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741, 15451,
15551, 16061, 16361, 16561, 16661, 17471, 17971, 18181, 18481, 19391, 19891, 19991
Si può notare che nella lista non vi sono primi palindromi di 2 o 4 cifre, fatta eccezione per 11,
quarto elemento della lista. Considerando il test di divisibilità per 11, si può facilmente
dedurre che tutti i numeri palindromi con un numero pari di cifre sono divisibili per 11 e,
quindi, non sono primi.
Non si sa se vi siano infiniti numeri primi palindromi in base 10. Ad aprile 2012 il più grande
primo palindromo conosciuto è 10290253 -2 · 10145126 -1 composto da 290253 cifre e scoperto da
Darren Bedwell.[1] Paulo Ribenboim attribuisce comunque a Harvey Dubner il titolo di principale
scopritore di primi palindromi grandi dal momento che la scoperta della maggior parte dei più
grandi numeri primi di questo tipo porta la sua "firma".
In binario, i primi palindromi più facili da trovare sono i primi di Mersenne, poiché sono anche
primi repunit. I primi 4 numeri primi palindromi in base 2, eccettuando i primi di Mersenne, sono 5
(101), 17 (10001), 73 (1001001) e 107 (1101011).
Ribenboim definisce primi triplamente palindromi quelli che, oltre ad essere palindromi, hanno
anche un numero di cifre che è un primo palindromo. Per esempio, 1011310 + 4661664 · 105652 + 1,
che ha 11311 cifre. O anche 11, essendo un primo palindromo ed essendo composto da due cifre. È
possibile che un primo triplamente palindromo in base 10 possa essere palindromo in qualche altra
base, per esempio nel sistema binario, ma sarebbe una coincidenza notevole se esso fosse
triplamente palindromo anche in quella base.”
2
In rosso il riferimento al problema della loro infinità, del quale ci
occuperemo in questo lavoro. Innanzitutto ci occuperemo della
loro forma numerica, della loro distribuzione e infine della nostra
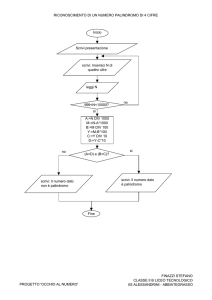
proposta di dimostrazione, basata sulla tecnica di:
- prendere un qualsiasi numero
- scriverlo al contrario (immagine speculare)
- togliere una cifra centrale, delle due uguali che ne risultano
- verificare se è primo (in tal caso, risulterà nella sequenza
A002385 dell'OEIS), fino a 19991. La nostra ipotesi è, come
vedremo, che tale lista sia infinita, se continuata dopo il suddetto
numero, formato, in base al metodo già parzialmente noto, dal
numero base :
199
scritto al contrario, diventa 991
incollato a destra 199, abbiamo il nuovo numero 199991, con due
cifre centrali uguali (in blu)
Ne togliamo una (in questo caso un 9) , rimane il numero 19991,
di cinque cifre,che è anche numero primo e quindi compreso nella
lista OEIS. (i numeri palindromi con un numero pari di cifre,
ricordiamo, non possono essere primi, perché sono divisibili per
3
11) .
Se prendiamo invece 173, abbiamo invece
173, 173371, meno una cifra centrale ripetuta, e abbiamo 17371,
che non è primo, e quindi non è nella lista.
(si può anche lasciare la cifra centrale, in tal caso si ha un altro
numero palindromo con un numero di cifre pari, e quindi non
primo (non esistono infatti primi palindromi con un numero pari
di cifre, tranne il numero 11, unica eccezione); le ripetizioni di
cifre sono consentite, infatti nella lista OEIS sono presenti numeri
primi con cifre ripetute, per esempio 13331, 15551, 19991 ecc.)
I numeri primi palindromi in base 10 sono quindi un sottoinsieme
infinito di tutti i numeri ottenuti con tale metodo, poichè infinito è
anche l’insieme dei numeri di tale forma palindroma generale
(tutti gli infiniti numeri n di c cifre possono essere trasformati in
numeri palindromi di 2c cifre se c di n è dispari, e di 2c cifre se c
di n è pari). Questo giustifica l’eccezione di 11, poichè 1 scritto al
contrario rimane 1 e aggiunto all’1 iniziale fa 11, numero primo.
Tutte le altre cifre singole, diventano numeri multipli di 11, che
non sono primi; per esempio 22, 33, 44, ecc. come accennato
anche nel testo di Wikipedia. Per i quadrati dei numeri repunit
4
abbiamo numeri palindromi ma non primi; essendo quadrati
11*11 = 121 palindromo di tre cifre ma non primo
111*111= 12321 palindromo di cinque cifre
1111*1111 = 1234321 palindromo di sette cifre
11111*11111=123454321 palindromo di nove cifre
111111*111111 = 12345654321 palindromo di undici cifre
1111111*1111111= 1234567654321 palindromo di 13 cifre
11111111*11111111=123456787654321 palindromo …
111111111*111111111=12345678987654321 palindromo …
1111111111*1111111111=12345678900987654321
palindromo …
Ora invece del 10, come cifre centrali abbiamo 9009
Per 11111111111^2 = 123456790120987654321, che non è più
palindromo; nella prima metà manca anche la cifra 8.
Ovviamente, per poter essere anche primi (ma non sempre), i
numeri palindromi con un numero dispari di cifre, debbono
iniziare e terminare con cifre dispari, tranne il 5 (altrimenti sono
multipli di 5 e quindi non primi).
Ma ritorniamo alla forma numerica 6k-1 oppure 6k +1 dei numeri
primi palindromi (tranne il 2 e il 3 iniziali). Ricordiamo la loro
5
sequenza:
2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929, 10301,
10501, 10601, 11311, 11411, 12421, 12721, 12821, 13331, 13831, 13931, 14341, 14741, 15451,
15551, 16061, 16361, 16561, 16661, 17471, 17971, 18181, 18481, 19391, 19891, 19991
Tabella 1
Numeri palindromi
primi
5
7
11
101
131
151
181
191
313
…
Forma 6k-1
Forma 6k+1
6*1 -1 = 5
6*1+1 = 5
6*2-1 =11
6*17-1 =101
6*22-1 = 131
6*25+1=151
6*30+1=181
6*32-1
6*52+1
…
…
Osservazioni: le forme aritmetiche dei numeri primi palindromi
sono miste, a differenza di altri tipi di numeri primi che sono solo
di una sola forma, come per esempio i numeri primi di Fermat (di
forma 6k - 1), per es. 5,17, 257; o di Mersenne (6k +1) , per
esempio 7, 31, 127, tranne il 3 iniziale in entrambi i casi, ecc.
Distribuzione
Circa la loro distribuzione fino a 10^n, importante per la
dimostrazione, vediamo che:
6
TABELLA 2
n
10^n
Numero di
primi
palindromi
Rapporto
crescente
p(N) /n
p(N)
1
2
3
10
100
1 000
4
5
20
4*n
2,5* n
6,66 *n
20
46
6,66*n
10,69*n
Da 1000 a 9999 ,
numeri di 4 cifre,
non ci sono primi
palindromi
4
≈ 4,3
5
10 000
20 000
100 000
…
…
Da 100 000 a
999999 non ci
sono palindromi,
poiche sono
numeri di 6 cifre
…
…
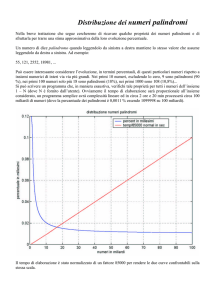
Poichè p(N) (da non confondere con p(n), partizioni di numeri)
cresce sempre più con N, sia pure irregolarmente, e anche e il
rapporto p(N)/n, ciò significa che il numero di primi palindromi
cresce all’infinito, e quindi che essi sono infiniti .
La lista OEIS non è disponibile sul Web e quindi non
possiamo vederne il relativo grafico; ma sarebbe stato interessante
notare come per potenze dispari di 10, essendo seguite da tutti
numeri pari, il grafico è piatto; per esempio da 10^3 = 1000 a
7
9999 non ci sono numeri palindromi (essendoci solo numeri con 4
cifre, e 4 è pari), e il grafico è piatto, mentre si ‘impenna” subito
dopo una potenza pari di 10, seguita da numeri con c numero di
cifre dispari, che consente l’esistenza di numeri primi palindromi:
per es. da 10^2= 100 fino a 999 ci sono ben quindici numeri primi
palindromi da, che sommati ai cinque numeri primi palindromi
fino a 100, abbiamo un totale di 20 fino a 1000, vedi Tabella 2.
Insomma si avrebbe un grafico a scalini , ma che comunque tende
all’infinito per i valori di y = P(n), il che mostra l’infinità dei
numeri palindromi in base 10 .
Inoltre con il metodo prima descritto possiamo creare tutti i
numeri palindromi che vogliamo (ovviamente solo con un numero
dispari di cifre), e poi testare se sono primi , e aggiungerli alla
loro lista, che su Wikipedia si ferma a 19991. Ma che, come
abbiamo provato a dimostrare, è infinita.
Attendiamo eventuali validi contributi e/o conferme (oppure
fondate smentite) da altri ricercatori sull’argomento.
Curiosità (Da Facebook, Numeri Primi DAY
Piramidi palindrome di numeri primi (con al centro sempre la
8
stessa cifra
5
5
7
151
353
757
31513
33533
327573
3315133
1335331
9375739
Altra piramide di palindromi (stessa fonte)
1. 7159123219517
371591232195173
33715912321951733
7337159123219517337
973371591232195173379
39733715912321951733793
3397337159123219517337933
933973371591232195173379339
39339733715912321951733793393
PIRAMIDI PALINDROME di numeri PRIMI
Dal sito
areeweb.polito.it/didattica/polymath/htmlS/info/Numeri/Mar09/M
ar09.htm - 23k
invece, riportiamo parzialmente :
“Dal Daily Telegraph, 21 febbraio 2002, il momento più palindromo del
secolo.
Anche fra i numeri ci sono i palindromi, che potremmo definire i “narcisi”
dei numeri, poiché si riflettono identici, come in uno specchio.
Il 2002 è stato un anno palindromo, come il 1991. Ed è raro che una persona
incontri due anni palindromi nel corso della sua vita. Un evento del genere
potrebbe capitare soltanto nel 2992 e 3003. Il prossimo anno palindromo
sarà invece il 2112.
In particolare sono oggetto di studio e di vaste indagini i palindromi che
sono anche numeri primi. Il più piccolo, a parte le nove cifre decimali, è 11
che è anche l’unico primo palindromo con un numero pari di cifre.
9
Tutti gli altri palindromi con un numero pari di cifre, sono infatti divisibili
per 11. E questo discende dal criterio di divisibilità per 11:
un numero è divisibile per 11 se la differenza tra la somma delle sue cifre di
posto dispari e quella delle cifre di posto pari è uguale a zero oppure è un
multiplo
di
11.
E per un palindromo con un numero pari di cifre la differenza fra le due
somme indicate è sempre zero. Ad esempio, 13579975531 è divisibile per 11 e
il risultato della divisione è 123454321.
I palindromi primi di tre cifre sono quindici: 101, 131, 151, 181, 191, 313, 353,
373, 383, 727, 757, 787, 797, 919 e 929. Non ne esistono con quattro o sei cifre,
mentre sono 93 a cinque cifre: 10301, 10501, 10601, 11311, 11411, 12421, …
Il più piccolo numero primo di sette cifre contenente soltanto le cifre 7 e 8 è
palindromo: 7778777. Il più piccolo numero primo palindromo che contenga
tutte e dieci le cifre decimali è 10234569878965543201.
Il più grande primo palindromo oggi noto è, al momento in cui vengono
scritte queste righe, quello scoperto da Harvey Dubner nell’aprile del 1999.
E’ un numero di 30803 cifre (anche questo è un numero primo palindromo)
che inizia è termina con 1; tra questi due 1 c’è una sequenza di zero, con al
centro un altro piccolo palindromo. Senza scrivere tutti gli zero, il numero è
il seguente:
1000..........0001110111000..........0001
Il record precedente era sempre di Dubner con il seguente numero, di 19391
cifre (ancora un numero primo palindromo) trovato nel gennaio dello stesso
anno:
1000..........0004300034000..........0001
Ancora qualche curiosità sui palindromi.
Il numero 795 559 265 009 384 106 è il più grande numero non palindromo il cui quadrato
sia un palindromo: 632 914 544 142 271 449 944 172 241 445 419 236.
Una somma di tre numeri
30 103 + 30 203 + 30 403 = 90 709
palindromi
che
è
ancora
un
palindromo:
Ed ecco una bella piramide di numeri palindromi primi, proposta da G. L. Honaker, Jr.
10
“
Commento:
come vediamo, ci sono numeri primi palindromi molto grandi:
anche questo è un indizio della loro infinità (a differenza dei
numeri primi di Fermat, che essendo rarissimi, rendono
molto difficile la dimostrazione della loro infinità).
Conclusioni
Possiamo concludere, dalle loro tabelle e dalle altre
considerazioni, che i numeri primi palindromi sono
infiniti, e quindi possiamo considerare il relativo problema
definitivamente risolto in senso positivo
11
Riferimenti
1) Numero primo palindromo, Wikipedia
2) Sito
areeweb.polito.it/didattica/polymath/htmlS/info/Numeri/Mar09/M
ar09.htm - 23k
Altre curiosità sui numeri palindromi (dal sito
www.matematicamente)
di Flavio Cimolin
Numeri palindromi
I numeri palindromi sono una di quelle curiosità che gli appassionati di matematica non
possono lasciarsi sfuggire. Tanto per rinfrescarci le idee, un numero è palindromo se può essere letto
indifferentemente da sinistra verso destra (come di solito facciamo) oppure da destra verso sinistra. Ad
esempio 357753 è un numero palindromo, così come 1288821.
Vediamo una prima cosa divertente: scriviamo in fila a partire da 1 un numero pari di numeri consecutivi,
ad esempio 123456. A questo punto rendiamo palindromo il numero ritornando nuovamente a 1: otteniamo
12345654321.
Il numero palindromo che abbiamo ottenuto è divisibile per 11, che è un numero palindromo.
Il quoziente della divisione è, guarda caso, un altro numero palindromo, nientepocodimeno che
1122332211.
Se dividiamo ancora questo numero per 11 otteniamo 102030201, ancora una volta un numero palindromo,
in cui fra ogni cifra sì è interposto uno zero!
Tra l'altro, i numeri 121, 12321, ... non sono nient'altro che le potenze successive di 11 (121=11^2,
12321=111^2, ...).
Alcuni (indubbiamente pazzi) matematici si sono tremendamente divertiti a trovare i più grandi numeri
quadrati, cubici, triangolari,... che siano dei palindromi.
Qualcuno indubbiamente proverà soddisfazione nello scoprire che il numero palindromo
4.211.672.540.455.378.958.718.869.999.688.178.598.735.540.452.761.124
12
un simpatico numero di 52 cifre, è un quadrato perfetto.
Meno interessante potrebbe invece essere sapere che 10.662.526.601 si ottiene elevando alla terza
potenza 2201.
Per non parlare del fatto che sommando tutti i numeri naturali da 1 a 3.654.345.456.545.434.563
(palindromo), si ottiene ancora un numero palindromo:
6.677.120.357.887.130.286.820.317.887.530.217.766.
Niente male, eh!
Fin qui, direte, è tutto frutto di ricerca al computer, e non c'è nulla di matematicamente interessante. E
invece, strano a dirsi, esiste una congettura tuttora indimostrata riguardante proprio i numeri palindromi.
Tutto nasce dalla seguente domanda:
"Prendi un numero, inverti le sue cifre e somma il numero che ottieni a quello iniziale. Se il risultato non è
un numero palindromo, ripeti il procedimento. E' vero che in questo modo partendo da qualunque numero
prima o poi si ottiene sempre un numero palindromo?"
Per capirci, prendiamo ad esempio il numero 87: 87 + 78 = 165; 165 + 561 = 726; 726 + 627 = 1353;
1353 + 3531 = 4884 .
In soli quattro passaggi abbiamo ottenuto il numero palindromo 4884 a partire dal numero originale 87.
Ma capita sempre così?
Se avrete la voglia di provare ad applicare il procedimento vi accorgerete ben presto che la maggior parte
dei numeri convergono effettivamente verso un numero palindromo in pochissimi passaggi, quindi si
potrebbe avanzare l'ipotesi che ciò accada in un numero finito di iterazioni per qualsiasi numero di partenza
scelto.
Ebbene, sembra essere così per praticamente tutti i numeri, tranne che per pochissimi di essi. Il più piccolo
numero che si “ostina” a non diventare palindromo è 196, e per questo il problema in questione è anche
noto come problema del 196. Sono state infatti calcolate al computer milioni e milioni di iterazioni del
procedimento senza riuscire ad ottenere un numero palindromo! Sembra proprio che il 196 sia un "numero
maledetto" per i palindromi.
In rosso le nostre correzioni, infatti nel testo originale era scritto
“Tra l'altro, i numeri 121, 12321, ... non sono nient'altro che le potenze successive di 11 (121=112,
12321=113, ...)”.
che caso mai doveva essere scritto cosi: 121= 11^2, 12321 = 111^2, e
13
12321 non è potenza di 11, ma di 111, essendone il quadrato.
FINE
14