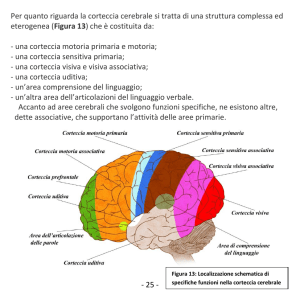
La struttura sub-riemanniana della
corteccia visiva
G. Citti - A. Sarti
http://www.vision.unibo.it
Milano, luglio 2004
struttura sub-riemanniana della corteccia V1
Completamento
modale e amodale
A. Sarti, G. Citti
p 1
struttura sub-riemanniana della corteccia V1
Modelli Fenomenologici
Mumford, Nitzberg, Shiota; Ambrosio,
Masnou; Morel; Bertalmio; Bellettini;
Modelli Neurofisiologici
Grossberg, Mingolla; Julesz;
Field,Heyes,Hess; Singer; Grey ;Lee
Modelli basati sui due approcci
Petitot, Tondut
A. Sarti, G. Citti
p 2
struttura sub-riemanniana della corteccia V1
Elastiche
γ̃ = (x, y) curva regolare
Z
y 00 x0 − x00 y 0
k = 02
(x + y 0 2 )3/2
2
1+k ,
γ̃
Mumford, Nitzberg, Shiota;
De Giorgi; Bellettini, Paolini: approssimazione
nel senso della Γ convergenza.
Modifiche del funzionale:
Z
1 + αφ(k),
γ
Se φ cresce linearmente, i minimi possono
essere continui, o avere spigoli.
A. Sarti, G. Citti
p 3
struttura sub-riemanniana della corteccia V1
Lifting di curve: Petitot - Tondut
1
0.8
0.6
θ
0.4
(x,y,θ)
0.2
0
−0.4
−0.6
(x,y)
−0.8
θ
−1
x
−1.2
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
y
γ̃(t) = (x(t), y(t))
x0 = cos(θ),
y 0 = sin(θ)
γ(t) = (x(t), y(t), θ(t))
Z q
length(γ) =
θ0 (t) = k
x0 2 + y 0 2 + θ 0 2
Z p
=
1 + k2
Le elastiche sono proiezioni 2D di minimi
vincolati in 3D.
A. Sarti, G. Citti
p 4
struttura sub-riemanniana della corteccia V1
L’algebra di rototraslazione
lifting e geometria subriemanniana [C. Sarti]:
γ 0 (t) = (cos(θ), sin(θ), k) = X1 + kX2
dove
X1 = cos(θ)∂x + sin(θ)∂y ,
X2 = ∂θ
X3 = [X2 , X1 ] = − sin(θ)∂x + cos(θ)∂y
Vale la proprieta’ di connettivita’
d((x, y, θ), (x̄, ȳ, θ̄)) = inf{length(γ) :
γ(0) = (x̄, ȳ, θ̄), γ(T ) = (x, y, θ)}
~ 1 + γ2 X
~ 2)
γ 0 (t) = (γ1 X
[Nagel, Stein, Wainger]
Le proiezioni 2D delle geodetiche del gruppo
sono elastiche
A. Sarti, G. Citti
p 5
struttura sub-riemanniana della corteccia V1
The Visual Path
A. Sarti, G. Citti
p 6
struttura sub-riemanniana della corteccia V1
Profili recettori delle cellule
semplici
filtri sensibili all’orentazione, a media nulla, e a
supporto compatto.
10
10
20
20
30
30
40
40
50
50
60
60
70
70
80
80
90
90
X1
100
X3
y
X
100
10
20
30
40
50
60
70
80
90
100
10
20
30
−
G(x,y,θ) (ξ, η) = X3 (θ)
e
40
50
60
70
80
90
100
(x−ξ)2 +(y−η)2
s
s
X3 (θ) = − sin θ∂ξ + cos θ∂η
A. Sarti, G. Citti
p 7
struttura sub-riemanniana della corteccia V1
La risposta ad una immagine
10
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
90
100
I : M ⊂ R2 → R+
10
10
20
20
30
30
40
40
50
50
60
60
70
70
80
80
90
90
100
10
20
30
40
50
60
Z
70
O(x, y, θ) =
X3 (θ)
A. Sarti, G. Citti
100
80
90
100
10
20
30
40
50
60
70
80
90
100
G(x,y,θ) (ξ, η)I(ξ, η)dξdη =
e
2 +y 2
−x
s
s
? I = X3 (θ)Is
p 8
struttura sub-riemanniana della corteccia V1
Le fibre di cellule semplici
Sopra ogni punto c’e’ una intera fibra di cellule
semplici: The visual cortex is a contact bundle
[Hoffman]
F (x, y) = G(x, y, θ), θ ∈ [0, π]
10
10
20
20
30
30
40
40
50
50
60
60
70
70
80
80
90
90
100
100
10
20
30
40
50
60
70
80
90
100
10
10
20
20
30
30
40
40
50
50
60
60
70
70
80
80
90
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
90
100
90
100
100
10
20
30
40
50
60
70
80
90
100
10
10
20
20
30
30
40
40
50
50
60
60
70
70
80
80
90
90
100
100
10
20
30
40
50
60
70
80
90
100
10
10
20
20
30
30
40
40
50
50
60
60
70
70
80
80
90
90
100
100
10
A. Sarti, G. Citti
10
20
30
40
50
60
70
80
90
100
p 9
struttura sub-riemanniana della corteccia V1
La soppressione dei non massimali
10
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
90
100
O(x, y, θ̄) = max O(x, y, θ)
θ∈[0,π]
Σ = {(x, y, θ) : ∂θ O = 0, ∂θθ O(x, y, θ) < 0}
L’immagine e’ liftata ad una superficie
∂θ O = ∂θ (X3 Is ) = −X1 Is =
= − < (cos θ, sin θ), ∇Is >= 0
(cos θ, sin θ) e’ ortogonale al gradiente. Ogni
curva di livello e’ liftata come a pag 4.
A. Sarti, G. Citti
p 10
struttura sub-riemanniana della corteccia V1
Campi di associazione e curve
integrali
100
200
300
400
500
600
700
100
200
300
400
500
600
700
800
900
1000
1100
~ 1 + γ2 X
~ 2)
γ 0 (t) = (γ1 X
γ(0) = (x, y, θ)
~ 1 = (cos(θ), sin(θ), 0)
X
~ 2 = (0, 0, 1)
X
2.5
0.6
2
1.5
0.4
1
0.5
0.2
0
0
−0.5
−1
−0.2
−1.5
1
−2
−0.4
0
−2.5
−1
0
0.1
0.2
0.3
0.4
0.5
0.6
A. Sarti, G. Citti
0.7
0.8
0.9
1
−0.6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
p 11
struttura sub-riemanniana della corteccia V1
Operatori differenziali
1
Gradiente orizzontale: f ∈ CX
(Ω, R)
∇X u = (X1 u, X2 u) inR2 × S 1
1
non esiste X3 u
X3 = [X1 , X2 ]. Se u ∈ CX
Sezioni del tangente orizzontale f ∈ C 1 (Ω, HX)
divX (f1 , f2 ) = X1 f1 + X2 f2
Sublaplaciano
∆X u = X12 u + X22 u
Diffusione lungo le curve integrali dei campi
ut = ∆X u
A. Sarti, G. Citti
p 12
struttura sub-riemanniana della corteccia V1
Bibliografia essenziale
distanza:
[Nagel, Stein, Weinger],
soluzione fondamentale - stime locali:
[Rothshild Stein] [Sanchez Calle]
stime gaussiane in gruppi omogenei:
[Bonfiglioli, Lanconelli, Uguzzoni]
Nonlinear equations
[Citti, Lanconelli, Montanari],
viscosity solutions [Stroffolini, Manfredi]
Teorema di Dini, rettificabilita’
in gruppi omogenei di passo 2
[B.Franchi, R.Serapioni, F.Serra Cassano]
[L.Ambrosio, B.Kirchheim]
A. Sarti, G. Citti
p 13
struttura sub-riemanniana della corteccia V1
Algebre nilpotenti e non
Ammettono una stratificazione
g = V1 ⊕ V2 ,
V1 = span{X1 , X2 }
V2 = span{X3 }
and[V1 , V2 ] = {0}.
Dilatazioni
δλ (X1 ) = λX1 .
δλ (X3 ) = [λX1j , λX1i ] = λ2 X3
X1 = cos(θ)∂x + sin(θ)∂y
X2 = ∂θ
Non esistono dilatazioni. Se esistessero
X1 = [X3 , X2 ] = −[[X1 , X2 ], X2 ]
δλ (X1 ) = λ3 X1 .
A. Sarti, G. Citti
p 14
struttura sub-riemanniana della corteccia V1
Riduzione al caso nilpotente
X1ξ̄ = (cos(θ̄) − (θ − θ̄) sin(θ̄))∂x +
+(sin(θ̄) + (θ − θ̄) cos(θ̄))∂y
X2ξ̄ = ∂θ
X3ξ̄ = −[X1ξ̄ , X2ξ̄ ] = − sin(θ̄)∂x + cos(θ̄)∂y
Esiste un cambio di variabile Φξ̄ e vettori
X1H = ∂e1 + e2 ∂e3
X2H = ∂e2 − e1 ∂e3
generatori dell’algebra di Heisenberg, tali che
(Xiξ̄ u) ◦ Φξ̄ = XiH (u ◦ Φξ̄ )
dilatazioni approssimate
Φξ̄ ◦ δλ ◦ Φ−1
ξ̄
A. Sarti, G. Citti
p 15
struttura sub-riemanniana della corteccia V1
Parametrice della soluzione
fondamentale
La soluzione fondamentale di
∂t = ∆ξ̄ = X12ξ̄ + X22ξ̄ e’
Γξ̄ (z, t; ζ, τ ) = ΓH (Φθ̄ (z), t; Φθ̄ (ζ), τ ),
dove ΓH , soluzione fondamentale dell’operatore
del calore per Heisenberg e’ nota
esplicitamente.
Teorema La soluzione fondamentale Γ di
∂t = ∆X soddisfa
|(Γ − Γξ̄ )(z, t; ζ, τ )| ≤ (t − τ )1/2 Γξ̄ (z, t; ζ, τ )
¯ Inoltre
per z, ζ in un intorno di ξ.
d2 (z, ζ) C
0 ≤ Γ(z, t; ζ, τ ) ≤
exp −
Q/2
t−τ
(t − τ )
dove Q = 4, per ogni 0 ≤ t − τ ≤ T , for every
z, ζ.
A. Sarti, G. Citti
p 16
struttura sub-riemanniana della corteccia V1
Superfici regolari in gruppi
omogenei
Σ = {(x, y, θ) : v = 0, ∇X v 6= 0}
vettore normale ∇X v/|∇X v|
Teorema [Franchi Serapioni Serracassano] e’
definita implicitamente una funzione continua
θ. Problema aperto: regolarita di θ
Congettura: θ e’ regolare lungo le proiezioni
delle curve orizzontali che giacciono sulla
superficie
([Ambrosio Serracassano] nel caso omogeneo)
A. Sarti, G. Citti
p 17
struttura sub-riemanniana della corteccia V1
Teorema di Dini
in gruppi non omogenei
1
Teorema [· - Manfredini]v ∈ CX
(Ω),
Γ = {(x, y, θ) ∈ Ω : v(x, y, θ) = 0, ∂θ v(x, y, θ) > 0}
Allora esiste funzione implicita θ
2.5
0.6
2
1.5
0.4
1
0.5
0.2
0
0
−0.5
−1
−0.2
−1.5
1
−2
−0.4
0
−2.5
−1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
−0.6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Se γ e’ curva integrale di X1 + kX2 di punto
iniziale (x, y, θ(x, y)) e γ̃ e’ la proiezione su R2 ,
allora esiste
X1 f (x, y, θ(x, y))
Xθ (θ(x, y)) = (θ ◦ γ̃) (0) = −
X2 f (x, y, θ(x, y))
0
A. Sarti, G. Citti
p 18
struttura sub-riemanniana della corteccia V1
Curvatura di una superficie
regolare [C. Sarti]
∃!γ̃ :
γ̃ 0 = Xθ (γ̃)
Xθ = cos(θ(x, y))∂x + sin(θ(x, y)).
γ100 γ20 − γ200 γ10
KX (γ) = − 2
(γ1 + γ22 )3/2
Xi vXj v Xi Xj v
KX (Σ) = divX (νX ) = δij −
|DX v|2 |DX v|
Moto per curvatura:
Xi vXj v vt = δij −
Xi Xj v
|DX v|2
A. Sarti, G. Citti
p 19
struttura sub-riemanniana della corteccia V1
Il modello di completamento
[C. Sarti]
10
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
90
100
u = O
0
t=0
Σ0 = {(x, y, θ) : ∂θ u0 = 0, ∂θθ u0 < 0}
u(·, 0) = u0 δΣ0
A. Sarti, G. Citti
p 20
struttura sub-riemanniana della corteccia V1
Il modello di completamento
1) diffusione lungo i campi
∂ u = ∆ u in R2 × S 1 × [0, h]
t
X
u(·, 0) = u0 δΣ
0
2) concentrazione che distrugge la diffusione
normale e genera un moto per curvatura
Σ (h) = {ξ : ∂ u(ξ, h) = 0, ∂ 2 u < 0}
1
νΣ0
ν
√ Σ0
u1 (h) : Σ1 (h) → R u1 (h) = hu(h)
Al tempo t, dopo n passi di lunghezza h = t/n
abbiamo due successioni Σn (t), un (t).
Σn (t) e’ definita come level set.
Σn (t) → Σ(t) moto per curvatura di Σ0
un (t) → u(t) evoluzione di u0
Nel caso euclideo [Bence, Merriman, Osher]
[Evans]
A. Sarti, G. Citti
p 21
struttura sub-riemanniana della corteccia V1
Idea della prova
Nel gruppo e’ definita un’operazione di somma
⊕ che commuta con le derivazioni
Teorema Sia ξ0 = 0 ∈ Σ0 , ν0 la normale a Σ in
ξ0 . Sia s ∈ R tale che
ξ0 ⊕ stν ∈ Σ1
Allora
s = KX (ξ0 ) + o(1)
as t → 0
dove KX (ξ0 ) e’ la curvatura di Σ0
In altre parole l’incremento ’infinitesimo’ s in
direzione normale e’ pari alla curvatura
A. Sarti, G. Citti
p 22
struttura sub-riemanniana della corteccia V1
Dim locally Σ1 = {θ = h(x, y) : (x, y) ∈ Q0 },
Z
0 = X2 u(ξ) =
X2 Γ(ζ −1 ⊗ ξ, t)u0 (ζ)dσ(ζ) =
Σ
usando la parametrice
Z
=
X2 Γξ0 (ζ −1 ⊗ ξ, t)u0 (ζ)dσ(ζ) + O(e−t )
Σ∩C
se ν = X2 , ζ = (x, y, θ), ξ = (0, 0, −st)
(ζ −1 ⊗ ξ) = (∗, ∗, θ − st), parametrizzando
Z
p
X2 Γξ0 (x, y, h(x, y)−st, t) 1 + |∇h|2 +O(e−t )
=
Q0
√
usando le dilatazioni approssimate x = tp
y = tq,
Z
p
√
0=
X2 Γξ0 (tp, tq, h( tp, tq)−st) 1 + |∇h|2 +O(e−t )
R2
imponendo l’annullamento dello sviluppo di
Taylor
√
s = K(0) + O( t)
A. Sarti, G. Citti
p 23
struttura sub-riemanniana della corteccia V1
Macula cieca
10
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
90
A. Sarti, G. Citti
100
p 24
struttura sub-riemanniana della corteccia V1
10
20
30
40
50
60
70
80
90
100
10
20
30
40
50
60
70
80
A. Sarti, G. Citti
90
100
p 25
struttura sub-riemanniana della corteccia V1
50
100
150
200
250
300
350
50
100
A. Sarti, G. Citti
150
200
250
300
350
400
450
500
550
p 26
struttura sub-riemanniana della corteccia V1
A. Sarti, G. Citti
p 27
struttura sub-riemanniana della corteccia V1
Direzioni di ricerca
La struttura della corteccia e’ stata descritta
come varieta’ di contatto definita dalla forma
ω = cos(θ)dx + sin(θ)dy
E’ possibile rilevare altre features, per esempio
la scala, ovvero la dimensione dei campi
recettori. L’aggiunta di una variabile ambienta
il problema in una varieta’ simplettica,
descritta dalla forma
d(e−s ω).
A. Sarti, G. Citti
p 28