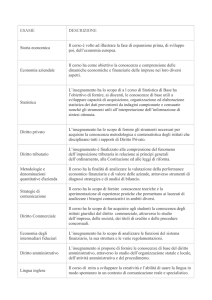
STATISTICA
STATISTICA…
IMBROGLIONA
Luce Clara
I S I S “A
I.S.I.S
A.Tilgher
Tilgher” Ercolano NA
Destinatari: Alunni della 3 classe della SS1G
e alunni del Biennio della SS”G
Gli alunni devono conoscere e saper
calcolare la media aritmetica
semplice e ponderata.
In appendice breve appunto sulla
media
Luce Clara
INDICE
LA STATISTICA PUÒ INGANNARE? TRILUSSA DICEVA “ SI!”
DIAP
5
NOTIZIE DAI GIORNALI:
SARANNO VERE?
DIAP
12
STRUMENTI CONTROL ’INGANNO:
INDICI DI VARIABILITÀ
À
DIAP
16
UN POLITICO INFURIATO…
DIAP
25
DIAP
27
QUALCHE NOZIONE SULLA MEDIA ARITMETICA
Luce Clara
Che cos
cos’è
è la statistica
Nata
N
t per d
descrivere
i
lle caratteristiche
tt i ti h
demografiche, economiche, … degli stati, è
l'insieme delle tecniche utilizzate per
raccogliere, elaborare e interpretare i
dati cche
da
e riguardano
gua da o co
collettività,
e
à, a
al fine
ed
di
studiare un fenomeno e poterne
prevedere gli sviluppi.
sviluppi
Luce Clara
• PROBLEMA MOLTO
IMPORTANTE: LA
MEDIA
RAPPRESENTA IL
FENOMENO CHE
STIAMO
STUDIANDO?
O la statistica ci p
può imbrogliare?
g
Luce Clara
STATISTICA!
Luce Clara
Sofia mangia
g DUE POLLI
Anna è digiuna
Luce Clara
STATISTICAMENTE
...
HANNO MANGIATO
UN POLLO
CIASCUNA!
LO DICE LA MEDIA ARITMETICA!
…e, se nun entra nelle spese tue, t'entra ne la statistica lo stesso
perch'è c'è un antro che ne magna due.
Trilussa
Luce Clara
LA STATISTICA
Sai che d'è la statistica? È na' cosa
che serve pe fa un conto in generale
de la gente che nasce, che sta male,
che more,, che va in carcere e che spósa.
p
Ma pè me la statistica curiosa
è dove c'entra la percentuale,
pè via che, lì, la media è sempre eguale
puro co' la persona bisognosa.
Me spiego: da li conti che se fanno
seconno le statistiche d
d'adesso
adesso
risurta che te tocca un pollo all'anno:
e, se nun entra nelle spese tue,
tt'entra
entra ne la statistica lo stesso
perch'è c'è un antro che ne magna due.
Trilussa
•
Luce Clara
REGIONE A
PERSONA
REGIONE B
REDDITO
PERSONA
REDDITO
A
1020
A
520
B
1200
B
650
C
1400
C
550
D
1080
D
780
E
1100
E
1600
F
1300
F
750
G
1250
G
1950
H
1150
H
1700
I
1250
I
1750
L
1350
L
1850
Luce Clara
TOTALE
12100
TOTALE
12100
Consideriamo il reddito
di 10 persone che abitano
in due regioni
Calcolate le due medie..
Cosa
possiamo
osservare?
LA MEDIA ARITMETICA DELLE 10 PERSONE è UGUALE ED è
PARI A 1210 EURO PROCAPITE
VUOL DIRE CHE IN MEDIA OGNI PERSONA GUADAGNA PIU’ O
MENO 1200 EURO
È FALSO,, CE NE
ACCORGIAMO
GUARDANDOLE LE 2
TABELLE!
IN PARTICOLARE LA REGIONE B PRESENTA
REDDITI MOLTO BASSI
Luce Clara
Leggiamo questa notizia:
Da un ‘i
D
‘indagine
d i statistica
t ti ti il reddito
ddit
medio della regione x e risultato essere
di 1150 euro procapite
SICURAMENTE DA UN PUNTO DI VISTA
MATEMATICO E
E’ ESATTO IL CALCOLO
DELLA MEDIA E GIUSTO MA……
Non avendo i dati di tutti i redditi non
possiamo dire se questo dato rappresenta la
realtà, o indica una situazione simile a
quella vista nella tabella della regione b:
redditi molto bassi e redditi molto alti
Luce Clara
la media è importante per la descrizione
sintetica di un fenomeno statistico
Ha però
H
ò il lilimite
it di non d
darcii alcuna
l
informazione sulla distribuzione dei dati
Luce Clara
NOTIZIA NON CHIARA PER UNO STATISTICO
Primo rialzo da giugno 2013 per il tasso di occupazione in
Italia. Si è attestato al 55,6%, aumentando dello 0,2% rispetto
ai dodici mesi prima
prima.
*
L’AUMENTO DELLO 0,2% È LO STESSO IN TUTTE LE
REGIONI?
È UGUALE AL SUD, AL CENTRO, AL NORD?
E SE L’AUMENTO FOSSE DELLO 05% AL NORD, DELLO
0,3% AL CENTRO E CI FOSSE STATA UNA DIMINUZIONE
DELLO 0,2% AL SUD (-2%)?
LA MEDIA NON REGISTREREBBE UN AUMENTO MEDIO
DELLO 0,2%,
0 2% CHE NON RAPPRESENTA LA REALTA
REALTA’?
?
*http://www.milanofinanza.it
http://www milanofinanza it
Luce Clara
NOTIZIA CHIARA PER UNO STATISTICO
Primo rialzo da giugno 2013 per il tasso di
occupazione in Italia. Si è attestato al 55,6%,
aumentando dello 0,2%
% rispetto ai dodici mesi prima.
I DATI SULL’AUMENTO PERCENTUALE SONO
RIPORTATI NELLA TABELLA SEGUENTE
REGIONI
AUMENTO /DIMINUZIONE PERCENTUALE DISOCCUPAZIONE
REGIONI DEL NORD
REGIONI DEL NORD
+0 5%
+0,5%
REGIONI DEL CENTRO
REGIONI DEL CENTRO
+0,3%
REGIONI DEL SUD E ISOLE
‐0,2%
Luce Clara
Ma i matematici hanno uno strumento…
strumento che
permette di capire la verità?
U strumento
Uno
t
t matematico……
t
ti
Quale?
GLI INDICI
DI
Variabilita
Variabilita’
Luce Clara
Esempio
In tre differenti prove di matematica 4 studenti
hanno riportato le seguenti valutazioni
1° studente
2° studente
t d t
3° studente
4° studente
media
1a Prova
3
5
8
9
6,25
2a Prova
5
7
6
7
6,25
3a Prova
6
7
6
6
6,25
In tutte e tre le prove la media è 6,25
ma i dati sono chiaramente distribuiti in modo diverso
Luce Clara
vo
oto
dispersione
9,5
9
5
9
8,5
8
7,5
7
6,5
6
5,5
5
45
4,5
4
3,5
3
2,5
2
1,5
1
0,5
0
1 studente
2 studente
3 studente
4 studente
0
1
2
numero prova
Luce Clara
3
4
1° studente
2° studente
3° studente
4° studente
media
1a Prova
3
5
8
9
6 25
6,25
2a Prova
5
7
6
7
6 25
6,25
3a Prova
6
7
6
6
6 25
6,25
• nel caso della 1a prova e 2a prova sarà
opportuno
oppo
tu o fare
aeu
un recupero
ecupe o pe
per a
alcuni
cu
studenti
• nel caso della 3a prova l’insegnante può
ritenere
it
che
h glili obiettivi
bi tti i siano
i
stati
t ti raggiunti
i ti
dalla classe, anche se ad un livello solo
sufficiente
Luce Clara
In statistica è possibile valutare in modo sintetico
l distribuzione
la
di t ib i
dei
d i dati
d ti mediante
di t gli
li indici
i di i di
variabilità (o dispersione)
Vedremo i seguenti indici
• Campo di variazione
•Varianza e scarto quadratico medio
•Scarto quadratico medio relativo
Luce Clara
Campo di variazione
E’ il più semplice degli indici di variazione:
Si calcola facendo la differenza tra il dato più
grande e il dato più piccolo
Campo variazione = x max – x min
Rappresenta
app ese ta l’ampiezza
a p e a dell’intervallo
de
te va o dei
de dati
dat
Luce Clara
Esempio
Consideriamo le valutazioni della pprima pprova
1° studente
2° studente
3° studente
4° studente
t d t
media
1a Prova
3
5
8
9
6,25
Xmax = 9;
X i =3
Xmin
Luce Clara
R
Range
=9–3=6
Calcoliamo il Range per tutte le tre prove
1a Prova
1° studente
2° studente
3° studente
4° studente
media
range
Range
g 1a pprova = 6
⇒
Range 3a prova = 1
⇒
2a Prova
3a Prova
3
5
8
9
2
7
8
8
6
7
6
6
6,25
6
6,25
6
6,25
1
dati ppiù dispersi,
p ,
risultati più eterogenei
dati più concentrati,
risultati più omogenei
Range 2a prova = Range 1a prova = 6 Stessa Distribuzione?
Luce Clara
Osservazioni:
1.. Il ccampo
po di
d variazione
v
o e dà
d informazioni
o
o sulla
su
distribuzione dei dati:
• più R è piccolo più i dati sono concentrati;
• più R è grande più i dati sono dispersi.
2. R è espresso nella stessa unità di misura dei dati
3. Tuttavia R tiene conto solo dei dati estremi della
distribuzione e non di tutti i dati, pertanto distribuzioni
diverse ma con gli stessi valori estremi hanno range
uguali
Es.
Range 1aprova = Range 2a prova.
ma distribuzione 1a prova ≠ Distribuzione 2a prova
Luce Clara
Varianza e Scarto quadratico medio
Sono gli indici di variabilità più utilizzati
utilizzati, e
tengono conto della distribuzione di tutti i dati.
Varianza
Rappresenta la media aritmetica dei quadrati
q adrati
delle distanze dei dati dalla media M
V i
Varianza
=σ
Luce Clara
2
(
x
=
1
) (
2
)
2
(
− x + x 2 − x + ..... + x n − x
n
)
2
Esempio - Varianza
Consideriamo le valutazioni della pprima pprova
1° studente
2° studente
2
3° studente
4° studente
media
1a Prova
3
5
8
9
6,25
(Δx1)2 = (3 – 6,25 )2 = 10,5625;
(Δx2)2 = (5 – 6,25 )2 = 1,5625;
(Δx3)2 = (8 – 6,25 )2 = 3,0625;
(Δx4)2 = (9 – 6,25 )2 = 7,5625;
σ2 = 10,5625+1,5625+3,0625+7,5625 = 5,6875
4
Luce Clara
Calcoliamo la Varianza per tutte le tre prove
1a Prova
1 studente
1°
2° studente
3° studente
4° st
studente
dente
media
varianza
2a Prova
3a Prova
3
5
8
9
2
7
8
8
6
7
6
6
6,25
5,69
6,25
6,19
6,25
0,19
Varianza 1approva = 5,69
⇒
Varianza 3a prova = 0,19
⇒
dati ppiù dispersi,
p
risultati più eterogenei
dati più concentrati,
risultati
i l i più
iù omogeneii
Varianza 2a pr. ≠ Varianza 3 pr “Le Distribuzioni Differiscono”
Luce Clara
Scarto quadratico medio o
Deviazione standard
È uguale alla radice quadrata della varianza
(x − x ) + (x
2
Scarto quadr.
quadr medio = σ =
1
Scarto quadr medio =
Luce Clara
2
∑ (x − x )
n
)
− x + ..... + xn − x
n
n
2
i
1
n
(
2
=
2
(
)
Δ
x
∑ i
1
n
)
2
Esempio - Scarto quadratico medio
Riprendiamo
p
le valutazioni della prima
p
prova
p
1a Prova
1° studente
2° studente
2
3° studente
4° studente
media
di
n
σ=
Luce Clara
∑ (Δx )
i
1
n
3
5
8
9
scarti da M
-3,25
-1
1,25
25
1,75
2,75
62
6,25
0 00
0,00
scarti2
10,5625
1 5625
1,5625
3,0625
7,5625
5,6875
68
2
= σ 2 = 5,6875 ≈ 2,3848
Calcoliamo lo Scarto quadratico medio per tutte le prove
1a Prova
1 studente
1°
2° studente
3° studente
4° studente
4
media
scarto
t quadratico
d ti
2a Prova
3
5
8
9
2
7
8
8
6
7
6
6
6,25
2 38
2,38
6,25
2 49
2,49
6,25
0 43
0,43
Scarto q. 1aprova = 2,38
⇒
Scarto qq. 3approva = 0,43
⇒
Scarto q. 1a pr. ≠ Scarto q. 1a pr
Luce Clara
3a Prova
dati più dispersi,
risultati più eterogenei
dati ppiù concentrati,
risultati più omogenei
“Le Distribuzioni Differiscono”
Osservazioni:
1. La varianza σ2 e lo scarto quadratico medio σ danno
informazioni sulla distribuzione dei dati:
• più σ2 e σ sono piccoli più i dati sono concentrati;
• più σ2 e σ sono grandi più i dati sono dispersi.
2. Entrambi gli indici tengono conto di tutti i dati della
distribuzione
Luce Clara
4. La varianza è espressa
p
mediante il qquadrato dell’unità
di misura dei dati
5. Lo scarto quadratico nella stessa unità di misura dei
dati e ppertanto viene ppreferito alla varianza
Luce Clara
SCARTO QUADRATICO MEDIO RELATIVO
Questo indice ha il vantaggio di essere compreso tra 0 ed 1
Più
σREL SI AVVICINA A ZERO
dati più concentrati,
risultati più omogenei
Più
σREL SI AVVICINA AD UNO
dati più dispersi,
Luce Clara
risultati
i l i più
iù eterogeneii
1 PROVA
3 PROVA
1 STUD.
1
STUD
2 STUD.
3 STUD.
4 STUD.
3
5
8
9
6
7
6
6
MEDIA
σ
σREL
6,25
6
25
2,38
0,61
6,25
6
25
0,43
0,11
CALCOLIAMO σREL
ricordando che
σx =scarto q
quadratico medio
μx= media aritmetica
n=numero dei dati
σREL (1 prova)=2,38/(6,25· √4-1)=
√
2,38/( 6,25·1,732)= 2,38/3,897=0,61
Luce Clara
L disoccupazione
La
di
i
è aumentata
t t in
i media
di dello
d ll 0,2
0 2 %,
%
È un buon risultato dateci fiducia,
nel prossimo quinquennio se ci rieleggerete
aumenterà
t à ancora
Ci può’ dire la fonte dei dati e un indice
di variazione? Magari lo scarto quadratico
relativo
l ti
Luce Clara
E adesso cosa dico? Uno scarto
Quadraticomedio relativo pari a 0,9?
Non credevo che nelle scuole insegnassero
Statististica !
Luce Clara
QUALCHE APPUNTO SULLA
MEDIA ARITMETICA
Luce Clara
•
•
•
•
•
•
•
•
Luce Clara
INDICI DI DIMENSIONE
Gli indici di dimensione danno l’espressione
l espressione sintetica di un fenomeno
quando i è rappresentato da un certo numero di osservazioni
quantitative. In altre parole essi permettono di sostituire un unico
significativo valore ad una serie di dati statistici.
Secondo Cauchy la media di un insieme di valori è un valore compreso
tra il minimo e il massimo.
In statistica si distinguono di solito due tipi di medie.
medie di calcolo: sono quelle che si calcolano tenendo conto di
tutti i valori della distribuzione;
1)M di aritmetica
1)Media
it ti
2) Media geometrica
3) Media armonica
4)) Media quadratica
medie di posizione; sono quelle che si calcolano tenendo conto
solo di alcuni valori della distribuzione
Mediana
2) Moda
• La media aritmetica
Si definisce media aritmetica di più numeri
quel valore che, sostituito ai dati, lascia
invariata la loro somma
IIndicando
di
d id
dati
ti con lle x la
l d
definizione
fi i i
di
media aritmetica semplice che si ricava è
x1 + x2 ..... + xn
M=
n
Esempio: 7, 8, 12, 15, 18 Ma = 60 / 5 = 12
Luce Clara
Nel caso di una distribuzione di frequenze ad esempio
Esempio: determinare l’età
media di 50 giovani presenti in
una pizzeria un sabato sera;
indichiamo con xi l’età e con yi
y
il numero di giovani per ogni
classe di età.
x1y1 + x2 y2 +.....+ xn yn
M=
N
Luce Clara
14*4 + 15*6 + 16*12 + 17*18 + 18*10
824
M = ————————————————— = —— = 16,48
50
50
Luce Clara