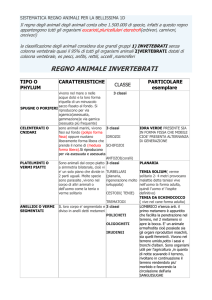
Università del Piemonte Orientale
Corsi di Laurea Triennale
Corso di Statistica e Biometria
Probabilità
Probabilità : valutazione della possibilità che accada (o sia accaduto)
un evento incerto.
Es.
! La probabilità di incontrare una persona conosciuta ieri
! La probabilità che domani piova
! La probabilità che la Juventus batta il Perugia alla prima partita di
campionato
! La probabilità di lanciare una moneta ed ottenere testa
! La probabilità che un bambino nato oggi viva almeno 80 anni
La stima della probabilità:
A priori:
• Simmetria (geometria): lancio di moneta o di dado, estrazione del
lotto
• Logica1 ‘se x è vero allora consegue che y deve essere pari
a….’
A posteriori
• Frequenza di un evento osservata in un numero molto alto di prove
• Limite della frequenza di un evento osservata per un numero di
prove tendente all’infinito
1
Corrisponde alla stima della probabilità conseguente alla formulazione di un’ipotesi. L’argomento sarà ripreso nelle prossime lezioni
probabilità di ottenere croce
0,7
0,6
0,5
prob.
0,4
prob.
0,3
0,2
0,1
0
0
20
40
60
n. lanci
80
100
120
La probabilità di un evento è compresa nell’intervallo
0 (evento impossibile)
-
1 (evento certo)
0 <= P(A) <= 1
La probabilità di due eventi mutuamente esclusivi è data dalle
somma delle probabilità di ciascuno dei due eventi
P(A o B) = P(A) + P(B)
Es. la probabilità di avere testa o croce ad un lancio di moneta è:
P (testa o croce) = P (testa) + P (croce) = 0,5 + 0,5
La probabilità di due eventi NON mutuamente esclusivi è data dalle
somma delle probabilità di ciascuno meno la probabilità che si
verifichino entrambi
P(A o B) = P(A) + P(B) – P(A e B) = P(A) + P(B) – P(A|B)
Es. la probabilità di avere un numero <=3 o un pari ad un lancio di
dado è:
P (<=3 o pari) = P (<=3) + P (pari) –P(<=3 e pari)=3/6 + 3/6 – 1/6=5/6
N.b. In questo esempio A e B sono eventi indipendenti quindi P(A|B) può essere
calcolato secondo le formule successive. Se A e B non fossero indipendenti il calcolo
dovrebbe tenere conto anche dell’associazione tra le due variabili.
Due eventi sono indipendenti quando la probabilità che accada il
primo non cambia la probabilità che accada il secondo.
P(A|B) = P(A|nonB)
La probabilità che sia estratto un numero del lotto non è influenzata
dal fatto che sia stato estratto la settimana precedente.
Se due eventi sono indipendenti, la probabilità che si verifichino
entrambi è data dal prodotto tra le probabilità che accada uno dei
due.
P(A e B) = P(A) P(B)
Es. la probabilità di estrarre una carta di cuori e che Baggio sbagli il
prossimo rigore
P(cuori e non-rigore) = P (cuori) P(non-r) = 4/40 x 1/5 = 1/50
Immaginiamo un esperimento su 300 mele prese a caso al mercato,
di cui 150 bianche e 150 rosse. 72 mele hanno un verme e 228 no.
Bianche
Rosse
Con verme
R1
Senza verme
R2
C1
C2
T
Se il colore delle mele e la probabilità di trovare un verme fossero
indipendenti, quale probabilità avremmo di avere una mela rossa con
un verme?
colore
Presenza di verme:
Bianche
Rosse
Con verme
72
Senza verme
228
150
150
300
P (mela rossa) = C2 / T = 150 / 300 = 0,5
P(verme) = R1 / T = 72 / 300 = 0,24
P(mela rossa e verme) = 0,5 x 0,24 = 0,12
colore
Bianche
Con verme
Rosse
0,24 x 0,5 = 0,12
0,24
Senza verme
0,76
0,5
0,5
1
Quante mele mi aspetto rosse e con verme?
colore
Bianche
Con verme
Rosse
0,12 x 300 = 36
72
Senza verme
228
150
150
300
Esercizio: completare la tabella
colore
Bianche
Con verme
Rosse
0,12 x 300 = 36
72
Senza verme
228
150
150
300