2-1
Teoria cinetica
del gas ideale mono-atomico
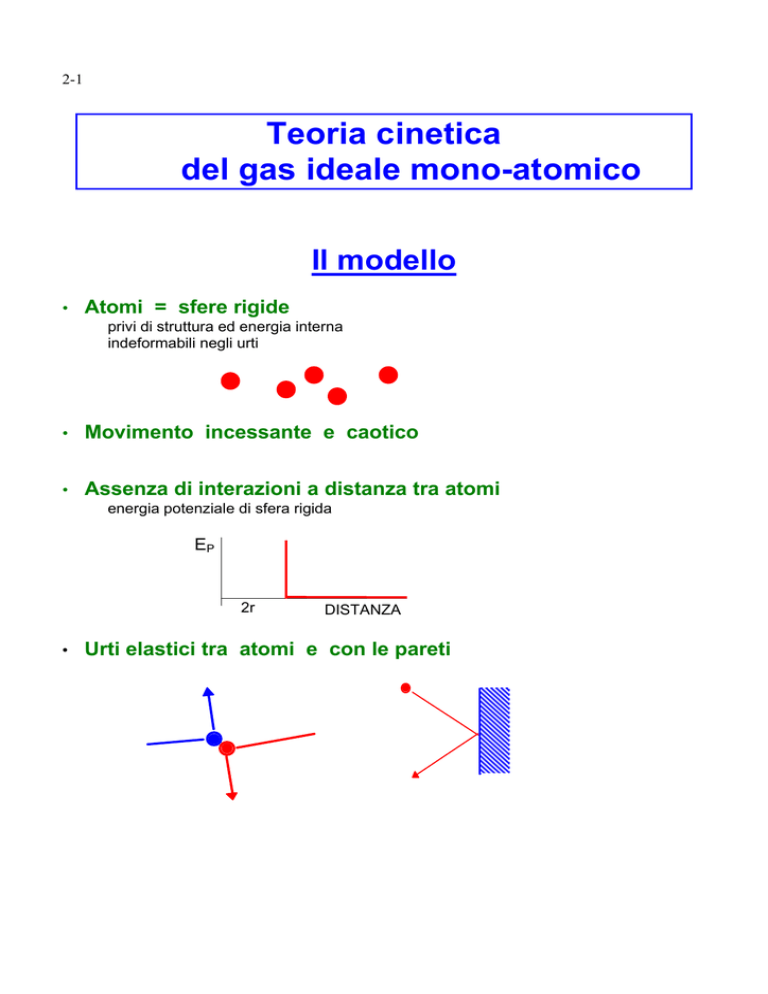
Il modello
•
Atomi = sfere rigide
privi di struttura ed energia interna
indeformabili negli urti
•
Movimento incessante e caotico
•
Assenza di interazioni a distanza tra atomi
energia potenziale di sfera rigida
EP
2r
•
DISTANZA
Urti elastici tra atomi e con le pareti
2-2
Moto di 1 molecola
q = mv
qx = mvx
X
-26
Esempio: N2 @ 300 K, 1 bar: m=4.6 x 10
Kg, <v>=500 m/s
qin
Urto elastico
con la parete
∆q
qout
x
∆qx = -2mvx =
−∆qx = 2mvx =
impulso subìto dalla molecola
impulso subìto dalla parete = J
Impulsi discreti nel tempo
2-3
N molecole
N grande:sovrapposizione di impulsi
effetto omogeneo e continuo
PRESSIONE = effetto medio degli urti
P =
F
=
A
J∆t
=
∆t ⋅ A
Nurti ⋅ J1
∆t ⋅ A
N urti 2mvx
=
A
∆t
N urti
1 vx ∆ t A N
=
V
2
∆t
∆t
A
fraz. di volume
di spessore vx∆t
vx ∆t
molecole con vx > 0
Ipotesi = tutte le molecole hanno la stessa velocità.
P
=
N
V
2
m vx
2-4
Media sulle velocità → pressione
Le molecole non hanno tutte la stessa velocità !
• Valori medi
v 2x
→
v2x =
1
N
∑v
• Isotropia
i
2
x,i
z
v
v
2
= v 2x + v 2y + v 2z = 3 v x2
x
• Pressione
P
=
1 N
m v2
3 V
=
2 N
Ek
3 V
Pressione = (densità) x (energia cinetica media)
• Equilibrio meccanico
P1
N1
V
Ek ,1
=
P2
N
= 2
V
Ek ,2
y
2-5
Temperatura
• Equazione di stato del gas ideale
macro
micro
pV = nRT
pV =
2
N Ek
3
n = n.o di moli = N/NA
R = 8.31 J/K/mol
T in kelvin
• La costante di Boltzmann
kB = R/NA = 1.380658x10-23 J/K [± 8.5 ppm]
pV
=
N kB T
=
2
N Ek
3
• Temperatura ed energia cinetica media
Ek
=
1
3
kB T
2
2
1
2
m v 2 = 32 k B T
1
m v 2x = k B T
2
• Equilibrio termico
T1 = T2
Ek ,1
=
E k ,2
2-6
Equilibrio termico
aspetti microscopici
• Mescolamento di aria calda e fredda
T1
T
T2
non equilibrio
equilibrio
Urti tra atomi del gas:
scambi di energia a livello microscopico
→
equalizzazione di <Ek> tra i due gas
•
Proprietà microscopiche all’equilibrio
(in assenza di forze esterne)
qualsiasi parte macroscopica ha
uguale densità
uguale valore di <Ek>
isotropia della velocità
distribuzione delle velocità ?
?
v
v
v
2-7
Facciamo il punto ...
• Risultati della teoria cinetica
Pressione
Energia interna
U = Σ Ek,i = N <Ek>
Temperatura
T ∝ <Ek>
Equilibrio termodinamico
• Cosa manca ?
Distribuzione delle velocità
Entropia
•
Limiti del modello
Atomi = sfere rigide, Estr=0
gas molecolari ? U ? T ?
Assenza di interazioni a distanza, Ep(i,j) = 0
gas reali ? U ? T ?
stati condensati ? U ? T ?
Urti elastici tra atomi, Estr=0
struttura interna degli atomi ? U ? T ?
Urti elastici con le pareti
all’equilibrio: situazione media
fuori equilibrio: scambi di energia
Ô calore e lavoro
2-8
Calore e lavoro
• Calore
T2
T1
Q
GAS
moto atomico
traslazionale
caotico
PARETE
moto atomico
vibrazionale
caotico
urti atomici
GAS
moto atomico
traslazionale
caotico
urti atomici
• Lavoro
w
GAS
moto atomico
traslazionale
caotico
PISTONE
moto macroscopico
traslazionale
urti atomici