Riassunto delle puntate precedenti:
Definizioni (informali) di enunciato e argomento
Definizione (informale) di argomento corretto
Definizione (formale) del linguaggio della logica enunciativa.
Definizione (formale) del concetto di formula ben formata del
linguaggio della logica enunciativa.
Definizione (formale) dell’algoritmo delle tavole di verità.
Estensione della logica enunciativa:
la logica dei predicati (o predicativa o del primo ordine)
Con la logica dei predicati è possibile trattare la struttura
logica di argomenti più complessi, in particolare di argomenti
che contengono importanti operatori logici detti quantificatori
(operatori che determinano l’estensione dell’insieme di oggetti
che soddisfano una certa proprietà).
L’introduzione del linguaggio enunciativo permette di fornire
un’analisi logica astratta di un’ampia classe di enunciati e
delle loro condizioni di verità.
Questo consente a sua volta di verificare la correttezza di
argomenti che abbiano come premesse e conclusioni un certo
numero di enunciati.
Riprendiamo tuttavia l’argomentazione
Tutti gli uomini sono mortali
Socrate è un uomo
quindi
Socrate è mortale
e chiediamoci:
1) è possibile tradurre fedelmente l’argomentazione nel linguaggio
enunciativo?
2) se è possibile, la traduzione è in grado di conservare la validità
dell’argomento?
Traduzione in linguaggio enunciativo (LE)
Linguaggio naturale
LE
Tutti gli uomini sono mortali
Socrate è un uomo
quindi
Socrate è mortale
p
q
⇒
r
Questa traduzione è l’unica possibile: gli enunciati
dell’argomento sono atomici e devono quindi essere
rappresentate da singole variabili enunciative.
Conservazione della correttezza?
La traduzione in linguaggio enunciativo è dunque possibile:
ma conserva anche la correttezza?
Per la traduzione, conservare la correttezza significa che –
anche per l’argomento in LE – se le premesse sono vere
allora deve essere vera anche la conclusione.
In realtà, tutto ciò che può fare la traduzione è formulare gli
enunciati in linguaggio naturale come variabili enunciative, e
di per sé le semplici lettere p e q non sono ‘costrette’ a
implicare con necessità r.
In altri termini, non è contraddittorio ammettere che esista
un assegnazione di valori di verità a p, q e r tale che
p
V
q
V
⇒
r
Dove sta il problema?
F
Il problema sta nel fatto che, nel linguaggio enunciativo, p, q e r
devono essere rappresentate da variabili enunciative atomiche,
perché non contengono alcun connettivo.
Ma ciò che garantisce la validità dell’argomento
Tutti gli uomini sono mortali
Socrate è un uomo
quindi
Socrate è mortale
dipende proprio dalla struttura interna di queste proposizioni.
Per estendere l’insieme di enunciati che è possibile analizzare
dal punto di vista della logica, occorre allora analizzare la
struttura interna degli enunciati atomici.
Questo passo porterà ad estendere il linguaggio enunciativo
verso un nuovo linguaggio artificiale, capace di rendere conto
della validità di argomenti come
Tutti gli uomini sono mortali
Socrate è un uomo
quindi
Socrate è mortale
Per analizzare la struttura interna di un enunciato atomico,
ricorreremo a uno strumento di antica tradizione, lo schema
soggetto-predicato.
Consideriamo il semplice enunciato “l’erba è verde”: in base allo
schema soggetto-predicato, avremo
“erba” → soggetto
“essere verde” → predicato
Il ‘predicato’ non è altro che una proprietà attribuita al soggetto.
Enunciati come “l’erba è verde” non sono tuttavia l’unico tipo
di enunciati di cui possiamo indagare la struttura interna.
Consideriamo infatti un enunciato come
“Mario è più alto di Carlo”
Un’applicazione
prescriverebbe
dello
schema
soggetto-predicato
“Mario” → soggetto
“essere più alto di Carlo” → predicato
Il significato intuitivo dell’enunciato sembra però compatibile
anche con la scomposizione
“Carlo” → soggetto
“essere più basso di Mario” → predicato
Sembra dunque che uno stesso contenuto concettuale sia
associato a due enunciati con due soggetti diversi: con quale
criterio scegliere?
Contenuto concettuale dell’enunciato
soggetto: Mario
predicato: essere più alto
di Carlo
?
soggetto: Carlo
predicato: essere più
basso di Mario
Soluzione naturale: il contenuto concettuale dell’enunciato
riguarda una relazione tra due soggetti. Questo implica che lo
schema dovrà contemplare almeno due casi possibili:
Predicato attribuito a un soggetto: si tratta di una proprietà di
quel soggetto.
Predicato attribuito a n soggetti: si tratta di una relazione che
sussiste tra quei soggetti.
Una generica proposizione atomica può parlare allora di uno
o più soggetti: si definisce termine singolare ogni
espressione che si riferisca a un soggetto singolo.
Termini Singolari
Nomi propri (“Mario”, “Carlo”, ecc.)
Pronomi dimostrativi ed espressioni che cominciano con un
aggettivo dimostrativo (“questo”, “quel tavolo”)
Pronomi personali singolari (“io”, “egli”, ecc.)
Descrizioni definite, vale a dire espressioni che cominciano
con un articolo determinativo singolare (“il presidente della
Repubblica”, “il sindaco di Berlino”, ecc.) e che hanno un
unico individuo come riferimento.
Consideriamo i seguenti esempi.
Mario è alto
Mario e Carlo sono fratelli
Mario è più alto di Carlo
Il predicato è ‘ciò che resta’ quando
dall’enunciato i termini singolari:
Mario è alto
Mario e Carlo sono fratelli
Mario è più alto di Carlo
vengono
eliminati
..... è alto
Predicato a 1 posto
(proprietà)
..... e ..... sono fratelli
Predicato a 2 posti
(relazione)
..... è più alto di .....
Predicato a 2 posti
(relazione)
Attenzione! La relazione ‘essere fratelli’ è
simmetrica (l’ordine non conta), mentre quella
‘essere più alto di’ non lo è.
La nozione di funtore
Abbiamo già incontrato la nozione di ‘descrizione definita’:
un’espressione come
Il presidente del Senato
denota un unico individuo e si comporta dunque ‘come’ un
termine singolare.
Possiamo però generalizzare la situazione e introdurre
un’espressione come
Il presidente di […]
Questa espressione può essere associata a una
‘operazione’ che associa a un certo gruppo l’individuo che
ne è il presidente.
Possiamo quindi rappresentare più in generale la situazione nel
modo seguente:
‘Il presidente di’ : R → S
dove
R = insieme delle istituzioni, S = insieme dei cittadini
In un caso particolare, possiamo quindi avere
Il presidente di
Il presidente del Senato
il Senato
Questo tipo di operazioni sono casi particolari di un concetto
più generale, quello di funzione.
Una funzione
f: S → T
è una corrispondenza tra due insiemi S e T, tale che a uno o più
elementi dell’insieme S associa uno e un solo elemento
dell’insieme T.
Data la notazione
f(x) = y, per x ∈S e y ∈T,
x è detto l’argomento della funzione e y è detto il valore della
funzione.
L’insieme S è detto dominio della funzione, mentre l’insieme T è
detto codominio della funzione.
Attenzione: la definizione appena fornita consente la possibilità
che S = T, cioè che dominio e codominio coincidano.
Esempio 1: Se
S = insieme dei bambini di una scuola elementare (con maestra
unica!)
T = insieme delle maestre della scuola
indichiamo con l’espressione
‘Maestra di’: S → T
la funzione che assegna a ogni bambino la sua maestra.
In questo caso S (il dominio) è diverso da T (il codominio).
Esempio 2
La funzione aritmetica ‘quadrato di’, che a ogni numero
naturale (positivo) n associa il numero naturale (positivo) n⋅n,
può essere rappresentata come
‘quadrato di’: N+ → N+
In questo caso, dominio e codominio coincidono.
Negli esempi 1 e 2, ciascuna funzione è definita per singoli
valori, ma è possibile definire funzioni per coppie di
argomenti.
Esempio 3
La funzione ‘somma di’ è definita per coppie di numeri: se con
N denotiamo l’insieme dei numeri naturali, la funzione
associa a ogni coppia di numeri naturali n, m il numero
naturale n + m.
La notazione è la seguente:
+ : {N x N} → N
+ : {n,m} → n+m
Torniamo al nostro argomento
Tutti gli uomini sono mortali
Socrate è un uomo
quindi
Socrate è mortale
Il linguaggio enunciativo non è in grado di esprimere la
struttura interna di nessuna delle proposizioni dell’argomento,
mentre lo schema soggetto-predicato ci permette di esprimere
la struttura della seconda premessa e della conclusione.
Come fare con la prima premessa?
Essa appare cruciale, perché esprime la validità di una
proprietà per tutti gli individui di un certo insieme.
Perché il linguaggio possa esprimere questo tipo di enunciati,
sarà necessaria una riformulazione dell’enunciato stesso nei
seguenti termini:
Per ogni possibile x, se x è un uomo allora x è mortale.
Questa riformulazione introduce due nozioni essenziali che
dovranno far parte del linguaggio:
le variabili
i quantificatori.
Una variabile non è altro che un termine singolare generico,
cioè un termine che può assumere valori diversi.
Quando per esempio si scrive
x+y = y+x,
si intende con ciò che quella uguaglianza è valida per
qualunque numero si decida di sostituire a x e y.
Un quantificatore è invece un operatore logico presente in
proposizioni che affermano per quanti individui di un dato
insieme valgono una certa proprietà o una certa relazione.
Saranno introdotti due quantificatori:
Quantificatore universale ∀
∀xPx → “per ogni x, x è P”
Quantificatore esistenziale ∃
∃xPx → “esiste un x che è P”
Linguaggio della logica predicativa (LP)
Alfabeto logico:
Connettivi enunciativi e quantificatori ∀, ∃
Alfabeto descrittivo:
AD-1) Un insieme infinito di variabili individuali x, y, z, ...
(eventualmente con apici e indici)
AD-2) Un insieme infinito di costanti individuali (eventualmente
con apici e indici)
AD-3) Un insieme infinito di costanti predicative P, Q, R, ...
(eventualmente con apici e indici)
AD-4) Un insieme infinito di costanti funtoriali f1, f2, ….
Alfabeto ausiliario: Parentesi e virgole
Definizione ricorsiva di termine individuale di LP
BASE: Sono termini individuali le variabili individuali e le costanti
individuali.
PASSO: Se t1, …, tn sono termini individuali e fn è una costante
funtoriale n-aria, anche fn(t1, …, tn) è un termine individuale.
CHIUSURA: Nient’altro è un termine individuale.
Esempi:
1) Se
‘Mario’ = termine individuale
‘zio di’ = costante funtoriale 1-aria,
allora
‘zio di (Mario)’ = termine individuale (il termine
dall’applicazione del funtore ‘zio di’ al termine ‘Mario’).
generato
2) Se
‘Carlo’, ‘Paola’ = termini individuali
‘Figlio unico di’ = costante funtoriale binaria (rappresenta la funzione
che assegna ai genitori di figlio unico l’individuo loro figlio)
allora
‘Figlio unico di (‘Carlo’, ‘Paola’)’ = termine individuale (il termine
generato dall’applicazione del funtore ‘Figlio unico di’ ai termini ‘Carlo’
e ‘Paola’).
Formule atomiche di LP
Se t1, …, tn sono termini individuali di LP e P è una costante
predicativa n-aria di LP, allora
P(t1, …, tn)
è una formula atomica di LP.
Esempio 1
‘Mario’ = m
(costante individuale)
‘Mario è alto’ = Am
‘è alto’ = A
(predicato a 1 posto)
formula atomica di LP
Attenzione!
Am è un esempio della forma generale
P(t1, …, tn ): infatti si pone P=A e t1 = m (in questo caso
n=1).
Esempio 2
‘Mario’, ‘Carlo’ = m, c
(costanti individuali)
‘Mario e Carlo sono
fratelli’ = F(m,c)
‘essere fratello’ = F
(predicato a 2 posti)
formula atomica di LP
Attenzione! F(m,c) è un esempio della forma generale
P(t1, …, tn): infatti si pone
P=F,
t1=m,
t2=c (in questo caso n=2).
Definizione ricorsiva di formula ben formata di LP
BASE: Ogni formula atomica di LP è una fbf di LP.
PASSO:
1) Se α è una fbf di LP, allora anche ¬ α è una fbf di LP.
2) Se α, β sono fbf di LP, allora anche α ∧ β è una fbf di LP.
3) Se α, β sono fbf di LP, allora anche α ∨ β è una fbf di LP.
4) Se α, β sono fbf di LP, allora anche α → β è una fbf di LP.
5) Se α è una fbf di LP e x una variabile individuale, allora anche ∀x α
è una fbf di LP.
6) Se α è una fbf di LP e x una variabile individuale, allora anche ∃ x α
è una fbf di LP.
CHIUSURA: Nient’altro è una fbf di LP.
Variabili libere e vincolate
In espressioni come ∀xα, ∃xα, la α potrebbe in generale contenere
altre variabili oltre a x. Se poniamo per esempio α = Px ∧ Qy, si
ottengono le fbf
[1] ∀x(Px ∧ Qy),
[2] ∃ x(Px ∧ Qy)
Esempi:
se P = predicato ROSSO e Q = predicato VERDE
[1]
∀x(Px ∧ Qy)
«Ogni cosa è rossa e y è verde»
[2]
∃ x(Px ∧ Qy)
«Esiste una cosa rossa e y è verde»
In generale, si dice che una variabile occorre vincolata quando
dipende da un quantificatore (da cui, appunto, è ‘vincolata’), e libera
altrimenti.
Nelle [1] e [2], cioè ∀x(Px ∧ Qy) e ∃ x(Px ∧ Qy)
la x occorre vincolata
la y occorre libera
Sempre la definizione di fbf in LP permette casi come ∀xPy, dove α =
Py. In questo caso, la quantificazione opera ‘a vuoto’ e si dice muta o
vacua.
Una formula α che contiene almeno un’occorrenza libera di una
variabile è detta formula aperta.
Una formula α che non contiene occorrenze libere di alcuna
variabile, cioè che
o non contiene alcuna variabile
o, se ne contiene, nessuna occorrenza di tali variabili in
è libera
è detta formula chiusa (= enunciato).
Esempi:
P(r,t)
∀x(Px∧Qs) ∃x∃
∃y(Px ∧ Qy)
sono formule chiuse, mentre
P(r,x)
sono formule aperte.
∀xPx ∧Qy ∃x∃
∃y(Px ∧Qy∧Rz)
α
Dati una formula α, un termine t e una variabile x, si dice
sostituzione di x con t in α la fbf che si ottiene rimpiazzando
uniformemente ogni occorrenza libera di x con t: tale fbf sarà
denotata dall’espressione
α[x/t]
Per esempio, data la fbf P(x) ↔ ¬ ¬P(x), la sostituzione in essa di x
con r è la fbf
P(r) ↔ ¬ ¬P(r).
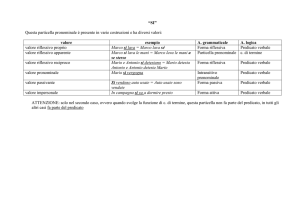
Linguaggio naturale
Linguaggio predicativo
Bruno = b, Carla = c, Aldo =a
amare = A, essere fabbro = F,
vedere = V, essere medico = M
«Bruno non ama niente»
∀x ¬ Abx
«Un fabbro si ama»
∃x (Fx ∧ Axx)
«Aldo vede ogni fabbro»
∀x (Fx → Vax)
«Se Bruno ama qualcosa,
allora ama qualsiasi cosa»
∃x Abx → ∀x Abx
oppure
¬∃
∃x Abx