Nucleosintesi stellare

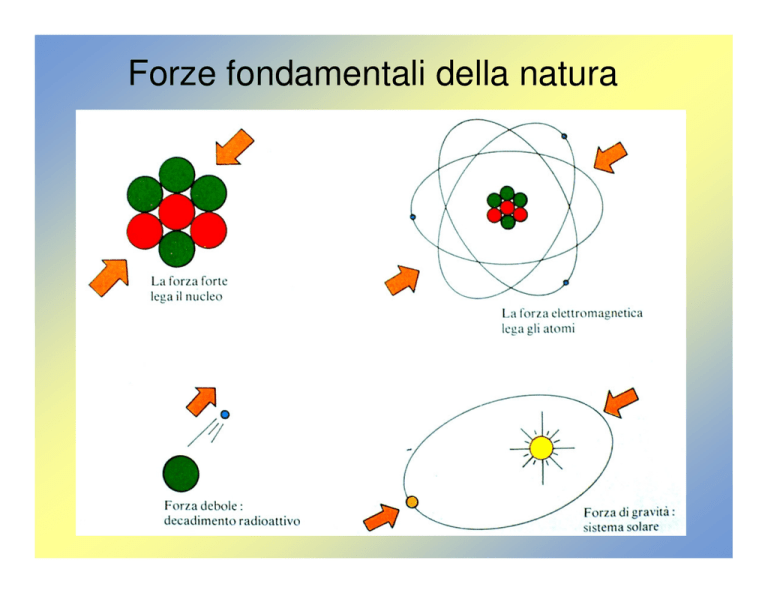
Forze fondamentali della natura
Difetto di massa ed Energia di legame nucleare
La massa di un qualsiasi nucleo, misurata con precisione per mezzo dello
spettrometro di massa, risulta inferiore alla somma delle masse dei
nucleoni componenti il nucleo stesso.
La massa dei nucleoni, non legati, è uguale a:
protone
1,00728 uma
neutrone
1,00867 uma
Considerando il nucleo del deuterio, formato da un protone e un
neutrone, la massa teorica risulta essere:
1,00728 + 1,00867 = 2,01595 uma
In realtà la massa sperimentale è uguale a 2,0130 uma, risultando
quindi inferiore a quella teorica per ∆m = 0,00295 uma
E = m·c2
(E)1 uma = (1,66 · 10-24 g) (9 · 1020 cm/sec) = 1,495 · 10-3 erg
e poiché 1 erg = 0,624 · 1012 eV, allora:
(E)1 uma = (1,495 · 10-3 erg) (0,624 · 1012 eV/erg) = 933 · 106 eV
= 933 MeV
(E nucl) MeV = 933 · ( ∆m )uma
Energia di legame media per nucleone
Per valutare la stabilità di un nucleo, anziché
considerare l’energia totale di legame, risulta
essere
particolarmente
significativa
ed
interessante l’energia media di legame per
nucleone ( nucl), che si calcola dividendo
l’energia totale per il numero dei nucleoni
componenti il nucleo.
Ponendo in ascissa il numero
di massa dei nuclidi e in
ordinata l’energia di legame
media per nucleo, si ottiene
un diagramma che descrive
L’ENERGIA DI LEGAME
MEDIA IN FUNZIONE
DEL NUMERO DI MASSA.
(
nucl) 1H
= 2,75 / 2 = 1,352 MeV
(
nucl) 2H
= 28,36 / 4 = 7,09 MeV
2
4
Fasce di stabilità e radioattività
Costruendo un grafico in cui si
riportano per i nuclidi naturali stabili
il numero di neutroni in ordinata e il
numero di protoni in ascissa, si
ottiene la fascia di stabilità.
I nuclidi, il cui punto
rappresentativo nel
diagramma cade
all’esterno della fascia
di radioattività,
risultano INSTABILI e
quindi danno luogo al
fenomeno della
radioattività.
Radiazioni
(potere di penetrazione = 100)
A-Z / Z > 1
1
0 n —>
14 C
1
β−
1p
—> 14 N + β− + v ¯
(potere di penetrazione = 1)
4
2 He
238
β+
alfa α
1
13
beta β
A-Z / Z < 1
1p
—> 10 n
N —> 13 C + β+ + v
(potere di penetrazione = 10000)
gamma γ
U —> 234 Th + α
99
0
0
γ
Tc —> 99 Tc + γ
A-Z / Z > 1
tipi di decadimento
Decadimento alfa
Es.:
238
U —> 234 Th + α
Il rapporto n/p cambia e si
avvicina alla stabilità:
1,587 prima; 1,543 dopo.
Raggi gamma
Es.:
99
Tc —> 99 Tc + γ
Decadimento beta -
Es.:
14 C
—> 14 N + β− + v ¯
Decadimento beta +
Es.:
13
N —>
13 C
+
β+
+v
β+ + e−
2 γ
Cattura elettronica
Es.:
44 Ti
+ e- —>
44 Sc
La cattura elettronica è
accompagnata dall’emissione
di RAGGI X.
Creagenti
v
1
Nel decadimento v e C sono
direttamente proporzionali.
V= - DC/DT
V= - dN/dT
= λ Nt
La cinetica è di 1°ordine :
v = k C
Vale la relazione:
N t = N 0 * e-λλt
1/2
T 1/2 = ln 2 / λ
(ln 2 = 0,693)
1/4
1/8
0
1
2
3
4
5 T 1/2
T 1/2 è tipico di ogni radionuclide
14
C = 5730 anni (utile per datare i fossili)
238
U = 4,5 *
109
anni
(utile per datare le
rocce)
Tempi di dimezzamento
Impieghi radioisotopi
Medicina
131
I
60
Co
32
P
Biologia
14
Geologia
C
235
U
60
Co
Industria
90
Aerospaziale Sr
238
Pu
Studio metabolismo tiroide e
trattamento tumori tiroide.
Terapia tumori.
Studio processi biologici.
Datazione fossili.
Datazione rocce.
Radiografia metalli (spessore).
Produzione energia elettrica
Sonde spaziali.
I - 131
Nucleosintesi stellare
Età dell’universo: 1,5 ÷ 1,8 · 1010 anni
BIG BANG
d = 1096 g/cm3
dopo 1 secondo:
dai 10 ai 100 secondi:
T = 1032 K
T = 1010 K,
fusioni nucleari di n e p.
comparsa di n, p, e.
E’ da questa materia che iniziarono a
condensarsi le stelle dando così il via alla
sintesi degli elementi chimici; tale
nucleosintesi non è comunque molto
progredita in quanto H ed He
rappresentano attualmente il 99% della
massa dell’universo.
formazione di ELIO (25%della massa
totale) e DEUTERIO (0,001%)
[materia rimanente: IDROGENO]
Evoluzione stellare
• Stadio di protostella: la forza gravitazionale trasforma un
ammasso di gas e polveri rarefatti.
• Stadio di stella stabile: la fusione nucleare di H contrasta
la contrazione gravitazionale.
• Stadio di gigante rossa: contrazioni e dilatazioni si
alternano per innesco di nuove reazioni di fusione.
• Stadio finale: la forza gravitazionale vince nel nucleo
stellare e origina una nana bianca o una stella a neutroni.
LA NUCLEOSINTESI AVVIENE NELLE STELLE.
Protostella
La materia fredda e rarefatta di una nube interstellare può
originare stelle per collasso gravitazionale.
Composizione: 92% H, 7% He, 1% altri elementi e composti
inorganici e organici (es. metano, metanolo, etene, metanale,
metilammina, acido metanoico).
Densità: 108 particelle / m3 (circa 10-21 Kg / m3).
Temperatura: 100 K.
La contrazione accelera la rotazione (mvr = K) e arroventa la
materia (legge di Wien) .
Le stelle nascono a gruppi (per una tipica
nube interstellare Mcritica = 3000 massa solare).
Fusione
Sole:
E’ il processo che
stabilizza le stelle e ne
giustifica la emissione
di energia radiante
5,2 . 1024
Kcal /min
1
1H
2
3
1H
+
1
+
1 H
1
2 He +
1H
3
—>
2
—>
3 He
2
2 He —>
1 H + β+
4
1 H
He
+
2
2
1
reazione globale: 4 11 H —>
L’energia liberata deriva da
aumento di ∆ m / nucleone
(aumento Elegame).
4 He
2
Gli elementi naturali fino a Fe si sono prodotti nelle stelle per fusione nucleare.
Fusione
Fusione del protone
Rappresentazione schematica della
struttura del sole: essa mostra come
variano la temperatura e la massa in
funzione del raggio solare.
Evoluzione di una stella
Rappresentazione schematica dell’evoluzione stellare dalla sequenza principale
allo stadio di gigante rossa per una stella di massa pari a quella solare.
fusione dell’idrogeno
- sequenza principale
τ ∼ 1010 anni
fusione dell’elio –
Gigante Rossa
τ ∼ 108 anni
Il nuclide della fusione del protone
nella sequenza principale si trasforma
nel nuclide 4He. Quest’ultimo può
eventualmente subire una fusione
dell’elio, portando ad uno strato di
gas fortemente espanso nello stadio di
gigante rossa.
Le stelle di massa ridotta diventano
nane bianche mentre le stelle più
pesanti sono soggette a stadi più
avanzati di evoluzione nucleare.
Fusione dell’elio nelle stelle giganti rosse.
Schema di una supernova
Rappresentazione schematica di una
struttura stellare all’inizio dello stadio
di supernova.
Per ogni strato sono riportati i
processi di fusione nucleare. I
processi r sono associati alla
disintegrazione del nucleo di ferro
nella regione centrale della stella,
processo che libera neutroni.
Ciclo di vita di una stella
gas stellare,
Gravitazione
polveri etc.
Processo r (supernova)
Condensazione
( T, ρ )
Elementi pesanti
Miscelazione, Rotazione
Processo e : fusione del 28Si
56Fe
Corpi stellari
Nane bianche
(M, R, L, T)
Fusione dell’idrogeno (sequenza principale)
4 1H
Fusione di C e O
(basso M)
4He
PPI, PPII, PPIII, CNO
28Si, 32S
Fusione dell’elio (processo s Giganti Rosse)
3α
12C, 16O
Elementi pesanti
Stella stabile
La contrazione gravitazionale
aumenta d e T.
A T = 107 °K si innesca la fusione nucleare.
La pressione di radiazione
dddm
stabilizza la stella.
FUSIONE NUCLEARE:
Fe
4 1H —>
4
He
mi > mf
mi - mf = ddm
ddm = E
He
ddm 1 uma = 933 MeV
H
56
A
Vale infatti:
E = m c2
Fusione stellare
Il processo di fusione di idrogeno può avvenire
con l’intervento di un “ciclo catalitico”.
C
Esempio ciclo C-N (di Bethe):
+
12
+
1
14
7N+
1
15
7N
1
1
1H
13
6C
+
6C
1H
—>
—>
1H —>
1H
—>
+ β+
13 13
7 N6 C
14
7
N
15 15O
8 7N
+ β+
1612 O
86C
reazione globale: 4 11 H —>
+ 42He
4 He
2
Avviene nelle stelle di 2^ generazione a T = 2* 107 °K.
Gigante rossa
stabile
Si alternano cicli di compressione e dilatazione:
La contrazione gravitazionale prende il
sopravvento a esaurimento del combustibile
nucleare; aumentano d e T.
collasso
Al raggiungimento di ogni T di fusione si ha una
dilatazione, con perdita strati più esterni e
nucleosintesi di nuovi elementi fino a Fe.
s
FUSIONE tipica:
dilatazione
3
4
He —> 12 C
(tripla alfa)
Morte di una stella
Supernova:
300 milioni x luminosità Sole)
energia liberata > 100 milioni x
energia solare annua.
esplosione
Stella a neutroni: d = 100 ton / cm3
Tsup = 1 milione °K
r = 10 - 20 Km.
Terminate le reazioni di fusione fino al ferro, si possono verificare due alternative
principali:
• La contrazione gravitazionale porta a stadio di nana bianca (stato degenerato,
con d = 200.000) quando la massa è piccola
• La contrazione gravitazionale porta a stadio di stella a neutroni per implosione
del nucleo quando la massa è grande (1,44 m°); gli strati esterni raggiungono
temperature da impartire elevatissima Ec alle particelle superficiali, con esplosione
= supernova.
Avviene:
p + e —> n
collasso
Supernova
Le prime osservazioni di supernova: 1054 - Cinesi;
1572 - Keplero;
1604 - Tycho Brahe.
1987 - (analisi sperimentale)
esplosione
L’alta concentrazione di neutroni permette la formazione
degli elementi pesanti per cattura neutronica.
Es.:
56
59
Fe + n —> 57 Fe + n —> 58 Fe + n —>59 Fe
Fe è instabile e decade β- :
59
Fe —>59 Co + β(avviene subito prima della esplosione)
Il 90% della massa viene restituito come materia
nebulare per essere riciclato in cicli stellari successivi
Supernova 1054
l’onda d’urto provocata può
catalizzare la nascita di nuove stelle
frequenza nella Galassia:
1 evento / 50 anni
" Supernova dei Cinesi " :
• comparsa nel Toro in luglio 1054 (a 6500 al);
• visibilità in pieno giorno per 23 gg;
esplosione
• scomparsa (?) in aprile 1056.
Messier (1750) avvistò i resti superficiali:
Crab Nebula in espansione da circa 9 secoli;
Zwicky (1933) previde i resti interni: stella di
neutroni.
Baade (1942) trovò una stella pulsar al centro della
Crab Nebula (30 guizzi/sec): e- a v —> c
spiraleggianti intorno a linee di forza di campi
magnetici (= radiazioni di sincrotone).
E = m·c2
(E)1g = 1 · (3 · 1010)2 = 9 · 1020 erg/g
(E)1 nucleo = (2,274 · 10-25 g/nucleo) (9 · 1020 erg/g) = 2,047 · 10-4 erg/nucleo
(E)1 mole = (0,1369 g/mol) (9 · 1020 erg/g) = 1,232 · 1020 erg/mol
(E)1 uma = (1,66 · 10-24 g) (9 · 1020 cm/sec) = 1,495 · 10-3 erg
e poiché 1 erg = 0,624 · 1012 eV, allora:
(E)1 uma = (1,495 · 10-3 erg) (0,624 · 1012 eV/erg) = 933 · 106 eV
= 933 MeV