Analisi di dati di frequenza

04/06/2015
Analisi di dati di frequenza
Fase di raccolta dei dati…
Fase di memorizzazione dei dati in un foglio elettronico…
0
1
1
1
04/06/2015
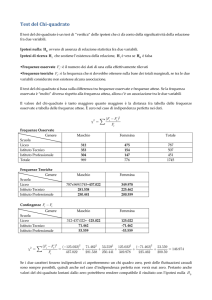
Frequenze attese uguali
Si assuma che dalle risposte al questionario sullo stato civile, la distribuzione delle risposte
sia stata quella riportata in tabella:
Stato Civile
Freq.assol.
Celibe/Nubile
34
Coniugato/Convivente
27
Separato/Divorziato
39
C’è una evidente differenza nella distribuzione delle frequenze?
45
Se le frequenze fossero uguali, allora
il loro valore numerico dovrebbe essere
40
35
30
34 27 39
33,3
3
25
20
15
10
5
0
Celibe/Nubile
Coniugato/Convivente
Separato/Divorziato
Grafico delle frequenze assolute
Se non ci fosse differenza nelle frequenze assolute, l’istogramma dovrebbe essere come
quello in blu nella figura:
Il test chi-quadrato misura le differenze
tra le barre blu e le barre rosse e consente di decidere se tali differenze sono
significative oppure no.
45
40
35
30
25
: 20
: 15
10
5
0
Celibe/Nubile
Coniugato/Convivente
Separato/Divorziato
! :∀
≠ :∃
≠ Le frequenze attese rappresentano il numero di dati atteso per ogni modalità (o
classe) se il modello teorico fosse vero.
Scegliere un opportuno errore di I tipo: # 0,05.
Scegliere un’opportuna statistica test:
v.a. chiquadrato
'( )
+,--./-0++1
− (
2! è vera
è una v.a. binomiale
3 = /5
2
04/06/2015
Costruire la regione di accettazione:
Se le frequenze osservate sono molto diverse dalle frequenze attese, allora le differenze
sono significative. Pertanto la statistica test assume valori elevati.
Se le frequenze osservate sono simili alle frequenze attese, allora le differenze non
sono significative. Pertanto la statistica test assume valori prossimi a zero.
Regione Critica
Il quantile per # 0,05
e k=3 vale ' ( (;!,CG=5,99.
' ( 5 − 1789899:à<5 . 9=
Determinare un campione casuale e valutare una stima puntuale della statistica
test:
>?@>>,> A
>>,>
(B@>>,> A
>>,>
+
>C@>>,> A
>>,>
= 2,18
Decidere se rigettare o meno l'ipotesi nulla, verificando se tale stima puntale
appartiene o meno alla regione di accettazione: 2,18 ∈ <0; 5,99=. Non si rigetta ! .
Frequenze attese diverse
Esempio: Si assuma che, alle elezioni politiche
Partito
% pregresse
precedenti, la distribuzione dei voti ricevuti dai
partiti A, B e C sia quella assegnata in tabella
A
0,48
(% pregresse). In seguito ad un exit pool, la
B
0,24
distribuzione dei voti delle elezioni che si stanno
svolgendo, è risultata essere quella relativa all’
C
0,28
ultima colonna. Stabilire se, in base ai risultati
degli exit pool, è plausibile ritenere che la distribuzione dei voti sia la stessa.
Freq.
osservate
39
31
30
Rispetto all’esempio precedente, le frequenze attese vanno calcolate in base alla distribuzione
teorica assegnata in I colonna.
Le frequenze attese rappresentano la media di una v.a. binomiale che conta il numero di
preferenze per ogni partito (classe), ossia 3 = Num.preferenze
per il partito…
H ~J 100; 0,48
HL ~J 100; 0,23
HM ~J 100; 0,39
Media
Freq.
attese
100K0,48
48
100K0,24
24
100K0,28
28
3
04/06/2015
Scegliere un opportuno errore di I tipo: # 0,05.
Calcolare il valore della statistica test:
'( )
+,--./-0++1
− (
>C@?N A
?N
>@(? A
(?
+
>!@(N A
(N
= 3,87
NB: Rispetto al caso precedente, le frequenze attese sono diverse.
Determinare la regione di accettazione: <0; ' ( (;!,CG =.
Decidere se rigettare o meno l'ipotesi nulla, verificando se 3,87 appartiene
o meno alla regione di accettazione: 3,87 ∈ 0; 5,99 : non si rigetta ! .
I due esempi forniscono una applicazione del test chi-quadrato, anche detto test per la
bontà di adattamento.
Il test chi-quadrato può essere applicato anche per variabili di tipo quantitativo.
Le frequenze attese vanno calcolate usando la formula31 K O H ∈ P1
P1 : 9 − 9; : 798Q9
Variabili quantitative discrete
Esempio: Da una rilevazione sugli incidenti stradali condotta per 65 settimane in un dato
tratto di autostrada, si è ottenuta la distribuzione di frequenza data in tabella:
No. Incidenti
0
1
2
3o+
Frequenza
48
15
2
0
Si verifichi l’ipotesi nulla che la v.a. generatrice ha legge di Poisson al livello di significatività
dell’1%.
E’ necessario acquisire informazioni sul parametro R che caratterizza la v.a. di Poisson.
Poiché il parametro R rappresenta la media, si usa la media campionaria per ottenere una
stima puntuale.
?NK!UGKU(K(
S̅ = 0,29
VG
Dalle tavole:
Le prob. sono
0,741 0,222 0,033 0,004
4
04/06/2015
Calcolare le frequenze attese31 65 K O<H 9=.
No. Incidenti
0
1
2
Frequenze osservate
48
15
2
Frequenze attese
48,17
14,43
65-48,17-14,43=2,40
Affinchè la somma delle frequenze attese sia uguale alla taglia del campione, la freq. attesa
dell’ultima classe va calcolata come − <3 3( =
L’errore di I tipo è: # 0,05.
Il valore della statistica test è: − (
?N@?N,B
'( )
?N,B
A
+,--./-0++1
G@?,?> A
?,?>
+
(@(,?! A
(,?!
= 0,098
Determinare la regione di accettazione: <0; ' (;!,CG =
No.classi-no.parametri stimati-1
Decidere se rigettare o meno l'ipotesi nulla, verificando se 0,098 appartiene
o meno alla regione di accettazione: 0,098 ∈ 0; 3,84 : non si rigetta ! .
Variabili quantitative continue
Se i dati del campione casuale sono forniti usando una distribuzione in tabella, il test chi-quadrato
è ancora la procedura più usata per verificare se il campione casuale proviene da una v.a. generatrice con distribuzione assegnata.
Esempio: Verificare se la statura di 400 individui selezionati a caso in una
certa città segue una distribuzione gaussiana. Si assuma che la media è 174 e
la varianza è 16.
Classi
Frequenza
<165
165-170
170-175
175-180
7
51
190
124
>180
28
Calcolare le frequenze attese31 400 K O<H ∈ P1 =
Per la prima classe è
O H X 165 O
H − 174 165 − 174
X
0,012
4
4
→ Z 400 K 0,012 4,8
Per la seconda classe è
O 165 X H X 170 O
VG@B?
?
X[X
VG@B?
?
0,147
→ Z( 400 K 0,147 58,8
5
04/06/2015
Per la terza classe è
O 170 X H X 175 O
Per la quarta classe è
O 175 X H X 180 O
Per la quinta classe è
170 − 174
175 − 174
X[X
0,440
4
4
→ Z> 400 K 0,440 176,0
BG@B?
?
X[X
N!@B?
?
0,334
→ Z? 400 K 0,334 133,6
O H > 180 O [ >
180 − 174
0,067
4
Classi
<165
165-170
170-175
175-180
>180
Frequenza osservata
7
51
190
124
28
Frequenza osservata
4,8
58,8
176,0
133,6
400-373,2=28,8
→ ZG 400 K 0,012 26,8
L’errore di I tipo è: # 0,05.
Il valore della statistica test è: '( )
+,--./-0++1
− (
B@?,N A
?,N
G@GN,N A
GN,N
+… +
(N@(V,N A
(V,N
= 3,9
Determinare la regione di accettazione: <0; ' ( ?;!,CG =
Decidere se rigettare o meno l'ipotesi nulla, verificando se 3,9 appartiene
o meno alla regione di accettazione: 3, 9 ∈ 0; 9,4877 : non si rigetta ! .
Test di Kolmogorov-Smirnov
Se i dati del campione casuale non sono forniti in tabella, conviene usare una procedura diversa: il test di Kolmogorov-Smirnov.
Il test di Kolmogorov-Smirnov consente di stabilire se due campioni provengono da due popolazioni aventi la medesima legge di probabilità
L’idea è quella di costruire le funzioni
di ripartizioni empiriche per i due campioni e poi di valutare la distanza massima tra queste ultime.
Nell’uso che faremo del test, un modello
è quello teorico, ipotizzato per la variabile
generatrice e l’altro è quello empirico.
! ] S ]! S Q79S
] S ≠ ]! S QS
Modello teorico
6
04/06/2015
Esempio: L’osservazione della durata (in ore) della batteria per cellulare di una data marca
in 24 esemplari di prodotto ha dato luogo ai seguenti risultati:
58,7
71,5
64,9
75,4
76,9
67,3
67,8
73,0
41,7 56,7 64,5 69,7 82,1 82,5 40,8
70,4 104 82,3 90,4 86,8 72,8 71,8
74,9
54,5
Per applicare il test di ipotesi sulla varianza, è stato necessario assumere che
la v.a. generatrice è gaussiana.
Verifichiamo se tale ipotesi è legittima.
I dati vanno ordinati.
40,8 41,7 54,5 56,7 58,7 64,5 64,9 67,3 67,8 69,7 70,4 71,5
71,8 72,8
73 74,9 75,4 76,9 82,1 82,3 82,5 86,8 90,4 104
Per ognuno di questi dati, è necessario calcolare il valore della funzione di
ripartizione del modello teorico: ossia gaussiano. ]! <S=~^<? , ? =
Per effettuare l’operazione di standardizzazione è necessario «stimare»
puntualmente media e varianza campionaria: S̅ 70,89 14,26.
La statistica test corrisponde al massimo delle differenze tra la funzione
di ripartizione empirica e la funzione di ripartizione teorica.
Dette quindi S<,= , …,S<a= le n osservazioni ordinate, la funzione di ripartizione empirica è
definita come
0

k
ˆ
Fn ( x ) = 
n
1
se x < x(1)
se x( k ) ≤ x < x( k +1)
se x ≥ x ( n )
La funzione di ripartizione empirica Fˆn ( x) è uno stimatore corretto di ]<S=
Poiché ]ca S stima la vera funzione di ripartizione F0 ( x ) , è logico basarsi su una qualche
distanza tra il modello teorico e il modello empirico.
La statistica test è la massima differenza (in valore assoluto) tra la funzione di ripartizione
empirica ]ba S e la funzione di ripartizione teorica ]! <S=
Dn = max
− ∞ < x < +∞
Fˆn ( x) − F0 ( x)
Se Fˆn ( x) e F0 ( x) sono vicine, si accetta l’ipotesi nulla.
Mentre se Fˆn ( x) e F0 ( x) sono lontane, l’ipotesi nulla va rifiutata.
?
Tabelle!!
7
04/06/2015
Il valore P nella tavola rappresenta il
complementare a 1 del livello di
significatività del test.
Le righe rappresentano la taglia del
campione casuale.
La regione di accettazione del test è
(0;0,26931), ossia valori della statistica
test inferiori a 0,26931, sono indicatori
di una sufficientemente limitata distanza
tra modello empirico e modello teorico.
Pertanto il campione casuale proviene
da una popolazione generatrice con
distribuzione gaussiana.
Questo risultato valida anche il test sulla varianza, poiché tra le ipotesi necessarie all’
applicazione del test c’è che la variabile generatrice abbia legge gaussiana.
8
04/06/2015
Esempio: L’osservazione della durata (in ore) della batteria per cellulare di una data marca
in 24 esemplari di prodotto ha dato luogo ai seguenti risultati:
58,7
71,5
64,9
75,4
76,9
67,3
67,8
73,0
41,7 56,7 64,5 69,7 82,1 82,5 40,8
70,4 104 82,3 90,4 86,8 72,8 71,8
74,9
54,5
E’ possibile costruire un normal plot per verificare anche graficamente che il
campione casuale ha andamento lineare.
40,8 0,020833
Dati ordinati
Il normal plot per un test grafico
1,2
1
0,8
0,6
0,4
0,2
0
0
20
40
60
80
100
120
41,7
54,5
56,7
58,7
64,5
64,9
67,3
67,8
69,7
70,4
71,5
71,8
72,8
73
74,9
75,4
76,9
82,1
82,3
82,5
86,8
90,4
104
0,0625
0,104167
0,145833
0,1875
0,229167
0,270833
0,3125
0,354167
0,395833
0,4375
0,479167
0,520833
0,5625
0,604167
0,645833
0,6875
0,729167
0,770833
0,8125
0,854167
0,895833
0,9375
0,979167
5 − 0,5
24
Verifica dell’ipotesi di indipendenza
Sia data la distribuzione doppia di frequenza relativa ad un campione casuale di individui
appartenenti alle forze lavoro per genere e condizione di occupazione.
Genere
Occupati
In cerca
Totale
Maschio
141
9
150
Femmina
69
11
80
Totale
210
20
230
Si vuole verificare se le variabili «forza lavoro» e «genere» sono indipendenti.
Sia d e 9 e , ] e ]9e , Z e Q e , f e f′
Questa procedura è già stata impiegata per calcolare l’indice di connessione di Cramer.
Genere
Occupati
In cerca
Totale
Maschio
61,30%
3,91%
65,22%
Femmina
30,00%
4,78%
34,78%
Totale
91,30%
8,70%
100%
Primo passo: costruire la distribuzione congiunta
9
04/06/2015
Se le variabili fossero indipendenti, gli eventi assegnati dovrebbero essere indipendenti.
Se gli eventi fossero indipendenti, allora O ] ∩ f =O ] O f
O d ∩ f =O d O f
O d ∩ Z =O d O Z
O ] ∩ Z =O ] O Z
Secondo passo: La distribuzione congiunta se le variabili fossero indipendenti è:
Genere
A
Occupati
Maschio 59,55%=65,22%×91,30%
Femmina
31,76%
Totale
91,30%
In cerca
Totale
5,67%
65,22%
3,02%
34,78%
8,70%
100%
Come nel caso del test chi-quadrato, è necessario misurare la «distanza» tra il modello
teorico A e il modello osservato B.
B
Genere
Occupati
In cerca
Totale
Maschio
61,30%
3,91%
65,22%
Femmina
30,00%
4,78%
34,78%
Totale
91,30%
8,70%
100%
Come nel caso del test chi-quadrato, è necessario confrontare le tabelle delle frequenze
assolute.
Terzo passo: E’ necessario calcolare le frequenze attese ed osservate.
FREQUENZE ATTESE
A
Genere
Occupati
In cerca
Totale
Maschio
59,55% K ijk ljm, nm
5,67% K 230=13,04
150
20
230
Femmina
Totale
31,76% K 230=73,04
210
3,02% K 230 6,96
80
FREQUENZE OSSERVATE
Genere
Maschio
B
Femmina
Totale
Occupati
61,30% K 230=141
30,00% K 230 69
210
In cerca
Totale
3,91% K 230 9
150
20
230
4,78% K 230 11
80
NB: le frequenze assolute marginali sono uguali sia nel modello A che nel modello B.
L’errore di I tipo è: # 0,05.
10
04/06/2015
Seguendo la procedura del test chi-quadrato il valore della statistica test è: .
'( )
+,--./-0++1
− (
?@>V,CV A
>V,CV
C@>,!? A
>,!?
+
VC@B>,!? A @V,CV A
+
B>,!?
V,CV
= 3,95
Nel calcolo dell’indice di connessione di Cramer, veniva effettuato il calcolo della differenza
tra le due tabelle A e B:
Genere
Occupati
In cerca
Maschio
4,04
-4,04
Femmina
-4,04
4,04
Le differenze così calcolate vanno normalizzate alle frequenze assolute costruite nella
tabella (A) e poi sommate al quadrato rispetto ai pesi della tabella (A).
Genere
Occupati
Maschio 4,04/136,96
Femmina -4,04/73,04
In cerca
-4,04/13,04
4,04/6,96
Il calcolo di Po è equivalente al calcolo della statistica chi-quadrato.
L’ indice di connessione di Cramér è un
indice relativo (che varia tra 0 e 1).
Il test chi-quadrato per l’indipendenza si
conclude mediante i seguenti passi:
Determinare la regione di accettazione: <0; ' ( <(@=K<(@=;!,CG =.
Mosaic-Plot
P∗o 3,95
0,017
230
In generale, la regione di accettazione
coinvolge il quantile di una variabile
aleatoria chi-quadrato con gradi di libertà
<. 97 − 1= K . − 1 .
Decidere se rigettare o meno l'ipotesi
nulla, verificando se 3,94 appartiene o
meno alla regione di accettazione:
3,95 ∈ 0; 3,84 : si rigetta ! .
11