Cinetica delle reazioni chimiche

5.1
Cinetica
delle reazioni chimiche
5.1.1 Aspetti introduttivi,
scopi e applicazioni
Ogni sistema chimico che si trovi in condizioni diverse da
quelle di equilibrio termodinamico tende a evolvere con una
sua velocità caratteristica verso tali condizioni. Il raggiungimento delle condizioni di equilibrio può richiedere dalle frazioni di secondo a molti anni, ma in ogni caso non è mai un
processo istantaneo. Il tempo necessario al compiersi di una
reazione chimica dipende dalla reazione considerata e dalle
condizioni nelle quali essa ha luogo. La cinetica chimica è
quindi quella branca della scienza che studia l’evoluzione temporale dei sistemi nei quali ha luogo una reazione, più comunemente indicati come sistemi reagenti. La conoscenza della
velocità di evoluzione del sistema reagente, indicata solitamente come velocità di reazione, ha una sua rilevanza tecnologica di estrema importanza in quanto fornisce un’informazione fondamentale per il corretto dimensionamento dei reattori chimici.
La letteratura scientifica riporta osservazioni sull’evoluzione temporale dei sistemi reagenti sin dalla prima metà del
19° secolo. Volendo precisare, la prima indagine quantitativa di una certa rilevanza fu lo studio della reazione di inversione del saccarosio a glucosio e fruttosio condotta da Ferdinand Wilhelmy nel 1850. Studi pionieristici importanti furono quelli condotti da Cato Guldberg e Peter Waage, che nel
1863 misero in rilievo la natura dinamica dell’equilibrio chimico, mentre poi Jacobus H. van’t Hoff stabilì che il rapporto tra le costanti cinetiche della reazione diretta e inversa fornisce il valore della costante di equilibrio termodinamico. La
formulazione delle cinetiche di secondo ordine, ossia di quelle reazioni la cui velocità dipende dal valore delle concentrazioni di due reagenti, fu l’oggetto degli studi di A.V. Harcourt e W. Esson, che negli anni compresi tra il 1865 e il 1867
studiarono la reazione tra il permanganato e l’acido ossalico; a essi si deve anche il primo studio delle reazioni consecutive. Sulla scia di questi esempi furono poi studiate altre
reazioni, quali l’esterificazione, la dissociazione dello ioduro di idrogeno e così via, in un continuo crescendo sino ai
giorni nostri.
Le reazioni consentono la trasformazione di alcune specie
chimiche (i reagenti) in altre (i prodotti). Esse sono solitamente indicate tramite delle notazioni formali del tipo:
VOLUME V / STRUMENTI
[1a]
reazione chimica
reagenti ⫺⫺
⫺⫺⫺⫺⫺⫺➤ prodotti
[1b]
aA + bB + ...⫺
⫺➤ cC + dD + ...
䉴
䉴
dove con le lettere maiuscole sono state indicate delle generiche specie chimiche e con i caratteri minuscoli i relativi coefficienti stechiometrici.
Dato che i fenomeni di trasporto di materia e di energia
hanno una notevole influenza sull’evoluzione di un sistema
reagente, gli studi cinetici sono solitamente condotti in condizioni in cui tali contributi risultano di importanza trascurabile
o, al limite, nulla. Queste condizioni idealizzate sono dette condizioni microcinetiche. Quando non sono realizzate, si parla
invece di condizioni macrocinetiche.
Le reazioni chimiche possono avvenire in sistemi sia omogenei che eterogenei. Per un sistema omogeneo, è definita come
velocità di reazione la quantità della specie i-esima che si produce globalmente, per effetto delle reazioni chimiche, per unità
di tempo e unità di volume di reazione. Per sistemi eterogenei,
invece, per maggior comodità si usa riferire la velocità di reazione all’unità di superficie interfasica o alla massa di catalizzatore anziché all’unità di volume di reazione.
Solitamente la velocità è indicata col simbolo Ri ed è funzione delle condizioni operative (temperatura e pressione) e
della composizione:
[2]
(
Ri = f T , P,C
)
Spesso, Ri è indicato anche come termine di produzione
specifico della specie i-esima, riservando il termine di velocità di reazione alla velocità delle singole reazioni che avvengono nel sistema in esame. Infatti, nei sistemi reagenti solitamente non ha luogo un’unica reazione ma un insieme più o
meno complesso di esse. Inoltre, anche quando possa essere
identificata un’unica reazione globale, molto spesso essa può
essere scomposta in un insieme di atti cinetici elementari, in
cui possono essere presenti connessioni tra le diverse specie
reagenti (ossia reazioni) in serie o in parallelo.
Quanto sopra evidenzia il problema alla base degli studi cinetici, ovvero la decodificazione del sistema in esame nelle diverse reazioni che intervengono nel processo. Ciò viene solitamente effettuato per via sperimentale cercando di identificare
tutti, o perlomeno i principali, intermedi di reazione. Infatti, gli
studi sulla velocità di reazione sono molto utili nel determinare
263
CINETICA E CATALISI
i singoli stadi del meccanismo della reazione stessa, anche se
è necessario integrare tali studi con altri approcci. L’elemento
più importante per determinare il meccanismo di una reazione resta comunque l’esatta identificazione di tutte le specie
chimiche in essa coinvolte, ricorrendo anche a informazioni
sulla stabilità delle specie individuate sperimentalmente nelle
condizioni di processo. In secondo luogo, l’attenzione può essere focalizzata sulle evidenze stereochimiche della reazione, per
esempio confrontando la stereochimica dei reagenti con quella dei prodotti. Molto spesso, per chiarire il meccanismo si fa
uso di molecole reagenti nelle quali un elemento sia sostituito da un suo isotopo, così da evidenziarne il cammino di reazione. Inoltre, nei meccanismi coinvolgenti più stadi, è molto
importante determinare quali siano le specie intermedie eventualmente formatesi. Se la reattività di queste è elevata, questo problema costituisce un’importante sfida per i metodi analitici. Spesso è possibile far riferimento a sistemi reagenti simili, dove è ragionevole assumere che piccoli cambiamenti della
struttura della molecola (per esempio un diverso sostituente in
una posizione di moderata influenza sul sito di reazione) non
influenzino apprezzabilmente il decorso della reazione. Infine, è utile confrontare le evidenze sperimentali con i risultati
di una elaborazione teorica, dato che oggi è possibile stimare
per via computazionale con ragionevole precisione, mediante
i metodi della meccanica quantistica, le costanti di velocità di
reazione così da ottenere un importante valore di confronto per
le misure sperimentali.
Una volta individuate, sperimentalmente o per via teorica,
tutte le specie chimiche presenti in un sistema reagente, lo schema cinetico, ossia l’insieme di reazioni che connette tra di loro
le varie specie chimiche, viene ricostruito mediante la scrittura di NR reazioni chimiche che sembrino le più qualificate per
descriverne l’evoluzione. Tali reazioni sono rappresentabili con
la scrittura compatta:
NC
[3]
∑ν A ⫽ 0
i =1
ij
i
dove NC è il numero di specie chimiche e Ai e nij indicano,
rispettivamente, l’i-esima specie chimica e il suo coefficiente
stechiometrico nella reazione j-esima. Solitamente si assumono coefficienti stechiometrici positivi per i prodotti della reazione e negativi per i reagenti. Se rij identifica la velocità con
la quale la specie Ai si forma nella j-esima reazione, in conseguenza delle reazioni stechiometriche si potrà scrivere
rNC
r1 j r2 j
j
[4]
=
==
= rj
ν1 j ν 2 j
ν NC
j
dove rj è chiamata velocità della j-esima reazione. Il termine
di produzione specifica dell’i-esima specie chimica Ri in funzione delle velocità delle singole reazioni presenti rj risulterà
quindi espresso come
NR
[5]
Ri = ∑ ν ij rj
j =1
Qualora nel sistema abbia luogo una sola reazione si verifica banalmente che Ri⫽ni r.
5.1.2 Metodi sperimentali
Poiché per ottenere dati cinetici è necessario misurare l’evoluzione nel tempo della composizione di un sistema, è evidente quale sia l’importanza di disporre di adeguati metodi di indagine
264
analitica. A titolo di esempio, si può citare il contributo che
l’evoluzione dei metodi spettroscopici non invasivi ha fornito
nell’identificazione di intermedi di reazione estremamente reattivi, quali le specie radicaliche, o di specie adsorbite su una
superficie. Ovviamente le tecniche analitiche sono scelte in
funzione del tipo di sistema reagente da analizzare, sia in termini di riconoscimento delle specie presenti sia nella misura
indiretta della composizione tramite la rilevazione di particolari proprietà fisiche della miscela quali, per esempio, la conducibilità elettrica, il potere rotatorio sulla luce polarizzata, il
colore o addirittura la viscosità o la densità. Uguale importanza hanno poi tutte le tecniche di campionamento supersonico
che consentono il prelievo di porzioni di fluido e l’invio allo
strumento analitico (tipicamente uno spettrometro di massa)
in tempi tali per cui il campione non abbia tempo di trasformarsi rispetto alle condizioni di reazione, o almeno di trasformarsi in misura tale da non perturbare significativamente il
risultato dell’analisi.
Un’altra importante caratteristica per ottenere buoni dati
cinetici è disporre di reattori in grado di fornire dati di composizione nel tempo non influenzati dalle condizioni fluidodinamiche esistenti al loro interno e in generale conoscere tutti
gli aspetti legati ai fenomeni di trasporto. Dato che i dati cinetici presentano una grande sensibilità alla temperatura è necessario che questi reattori siano realizzati in modo da poter operare nelle condizioni più prossime a quelle isoterme. Per questo motivo sono disponibili reattori chimici di laboratorio
opportunamente progettati per realizzare le condizioni microcinetiche e pertanto di tipo agitato. Qualora non sia possibile
conseguire un adeguato livello di agitazione, si ricorre anche
a configurazioni a ricircolazione esterna. Questi reattori, in
funzione del sistema considerato, possono operare con modalità discontinua o continua. Nel primo caso i valori di composizione saranno raccolti in funzione del tempo, mentre nel
secondo in funzione del tempo di residenza medio tR dei reagenti nel reattore. Quest’ultimo parametro è definito come il
rapporto tra il volume VR occupato dalla miscela reagente nel
reattore e la portata volumetrica Q di alimentazione allo stesso. Il bilancio materiale in questi sistemi assume la forma:
[6]
dCi CiF − Ci
=
+ Ri
tR
dt
dove con CiF⫺Ci si è indicata la differenza di concentrazione
della specie i-esima esistente tra entrata e uscita dal reattore.
Qualora il reattore operi in continuo e in condizioni stazionarie la velocità di reazione è direttamente misurabile tramite la
variazione di concentrazione tra entrata e uscita del reattore
stesso. Viceversa, in un reattore che operi in regime discontinuo (tR⫽⬁) la velocità di reazione risulterà espressa dalla derivata della concentrazione della specie nel tempo. In ogni caso
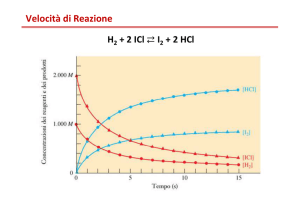
l’andamento qualitativo della composizione delle specie presenti sarà analogo a quello illustrato in fig. 1, dove sono riportate le concentrazioni di un reagente, un intermedio di reazione e un prodotto. Da quanto sopra si vede chiaramente che, se
si dispone di reattori attivi in condizioni di perfetta miscelazione, è conveniente operare in modo continuo per ricavare il
valore puntuale della velocità di reazione da una semplice misura di variazione di concentrazione.
Ottenuti i dati sperimentali di composizione, i valori delle
costanti cinetiche possono essere ricavati ricorrendo a due diversi approcci: il metodo differenziale e quello integrale. Il primo
consiste nel considerare due punti sufficientemente vicini, in
modo che la concentrazione non sia variata oltre qualche punto
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
reagente
prodotto finale
prodotto intermedio
assumere che la velocità del processo risulti proporzionale alla concentrazione della specie reagente:
r = kC A
concentrazione
[8]
•
processi bimolecolari del tipo A⫹B⫺ M⫹N, nei quali la
specie A reagisce con quella B per portare alla formazione dei prodotti della reazione. In questo caso è ragionevole assumere che la velocità del processo risulti proporzionale alla frequenza di collisione tra le due specie, che secondo la teoria cinetica dei gas è proporzionale al prodotto
delle loro concentrazioni:
䉴
r = kC AC B
[9]
tempo (o tempo di residenza)
fig. 1. Andamento tipico delle concentrazioni
delle specie chimiche coinvolte durante una reazione.
percentuale, e poi calcolare la derivata della concentrazione
tramite il rapporto incrementale (ossia DCi ⲐDt). Una volta ottenuti tali valori, essi vengono diagrammati in funzione della
concentrazione delle diverse specie, così da evidenziare i differenti andamenti, quali quello lineare, di potenza intera o razionale. Questo metodo è di semplice attuazione ma risente di
errori in quanto si approssima una derivata con il rapporto
incrementale calcolato su di un intervallo di tempo finito. Nel
metodo integrale, invece, si cerca di riprodurre le curve di composizione nel tempo globalmente, minimizzando l’errore tra i
punti sperimentali e quelli calcolati con un modello del reattore i cui parametri incogniti sono i valori delle costanti cinetiche. Per tale scopo, sono disponibili metodi di regressione
numerica che in modo efficiente minimizzano il valore di una
opportuna funzione obiettivo, che solitamente si identifica con
l’errore percentuale medio tra i valori calcolati e quelli sperimentali.
5.1.3 Espressioni della velocità
di reazione
•
processi trimolecolari del tipo A⫹B⫹T⫺ M⫹N⫹T, nei
quali la specie A reagisce con quella B per portare alla formazione dei prodotti della reazione. Nella reazione interviene anche una terza specie T che contribuisce alla ridistribuzione energetica conseguente la reazione. In questo
caso la velocità del processo risulta proporzionale, oltre
che alla frequenza di collisione tra le due specie principali, anche alla concentrazione del terzo corpo:
[10]
䉴
r = kC AC BCT
Occorre però precisare che l’evenienza di questi processi è estremamente rara a causa della bassissima probabilità di
un urto che coinvolga in contemporanea tre specie. Non si
riscontrano invece reazioni elementari con molecolarità superiore a tre.
In realtà, si verifica sovente che sia utile descrivere l’evoluzione di un sistema reagente tramite reazioni non elementari (ossia scomponibili in reazioni elementari a un successivo
esame). Le ragioni di ciò risiedono nel fatto che nella decodificazione di uno schema cinetico complesso di reazioni non
sempre è possibile, o non è computazionalmente conveniente,
fare intervenire nel processo le effettive reazioni elementari.
In altre parole, in questa evenienza, lo schema cinetico contiene delle reazioni di tipo globale, la cui velocità risulta espressa da relazioni algebriche più complesse di quelle sopra riportate. Sovente, per queste reazioni, si fa ricorso a espressioni
del tipo legge di potenza
NC
La velocità di una generica reazione j dipende in generale dalle
grandezze fisiche, temperatura e pressione, e dalle concentrazioni delle diverse specie presenti nel sistema. La relazione
fenomenologica che la esprime contiene una costante di proporzionalità kj che fornisce la dipendenza dalla temperatura e
una funzione più o meno complessa delle concentrazioni delle
specie chimiche coinvolte nella reazione Yj :
[7]
rj = k j (T ) ⋅ Y j (C )
Le reazioni su cui è formulato uno schema cinetico possono essere globali o elementari. Queste ultime coinvolgono
nell’atto reattivo direttamente i reagenti della reazione come
espresso nella loro equazione stechiometrica. Le reazioni globali sono viceversa decomponibili in un numero di stadi intermedi, tutti costituiti da reazioni elementari.
Generalmente, i processi elementari si identificano mediante la loro molecolarità, ossia un indice intero che identifica il
numero di specie coinvolte nella reazione. I più comuni tipi di
processi elementari sono i seguenti:
• processi monomolecolari del tipo A⫺ M⫹N, nei quali la
specie A subisce una trasformazione in virtù della quale
si isomerizza o si decompone. In tal caso è ragionevole
䉴
VOLUME V / STRUMENTI
[11]
rj = kj ∏ Ci ij
o
i =1
dove con l’esponente oij si indica l’ordine di reazione per la
specie i-esima nella j-esima reazione. Gli ordini di reazione
sono dei numeri razionali, che quindi possono essere anche
non interi e il cui valore è solitamente compreso nell’intervallo tra ⫺2 e ⫹3, anche se raramente si incontrano ordini di reazione superiori a 2. Essi riflettono espressioni cinetiche di tipo
funzione razionale, tipiche per esempio dei processi catalitici
eterogenei
[12]
rj =
kj CACB
1+ bACA + bBCB + bM CM
La somma degli ordini di reazione relativi ai singoli reagenti prende il nome di ordine di reazione globale della j-esima
reazione:
NC
[13]
oj = ∑ oij
i =1
Gli ordini di reazione sono determinati sperimentalmente e il loro valore è quindi distinto da quello dei coefficienti
stechiometrici nij . È facile vedere che, qualora la reazione sia
265
CINETICA E CATALISI
elementare (e solo in questo caso), l’ordine di reazione è legato
al coefficiente stechiometrico dei reagenti nel modo seguente:
−ν per i reagenti
oij =  ij
[14]
per i prodotti
 0
libera standard DG°j sia del prodotto delle attività delle singole specie elevate al rispettivo coefficiente stechiometrico:
Le reazioni chimiche, sia elementari sia globali, possono
essere irreversibili o reversibili a seconda della rilevanza della
reazione inversa. Qualora essa rivesta un’importanza non trascurabile, la velocità della reazione deve contenere i contributi sia della reazione diretta r៬j che di quella inversa rឈj
rj = rj − rj
[15]
È facile verificare che quando i valori delle attività si identificano con quelli di equilibrio, l’espressione [17] si annulla.
Dalla medesima equazione è facile ricavare l’espressione per
la reazione inversa mediante un semplice confronto con la [15]:
rj NC νij − ∆G j / RT
[19]
rj =
∏ a = rj e
K j i =1 i
Dato che all’equilibrio termodinamico la velocità della reazione globale deve essere nulla (rj⫽0), la velocità del processo
diretto deve uguagliare quello inverso. D’altra parte, la trattazione termodinamica dei sistemi reagenti porta alla seguente relazione tra la costante di equilibrio Kj e le attività ai delle specie chimiche in gioco in corrispondenza delle condizioni di equilibrio:
Risulta quindi che dalla conoscenza della condizione di equilibrio termodinamico e dall’espressione della velocità di reazione diretta è possibile ricavare quella della reazione inversa.
NC
[16]
NC
[18]
5.1.4 Dipendenza della costante cinetica
dalla temperatura
ν
i =1
La dipendenza dalla temperatura della costante di velocità di
reazione o costante cinetica segue, con buona approssimazione, l’espressione di Arrhenius:
Si ricorda che l’attività è definita come il rapporto tra la
fugacità fi della specie nelle condizioni operative in esame e
quella valutata in opportune condizioni di riferimento e ha
espressioni tipiche a seconda dello stato fisico del sistema in
esame. Per un sistema in fase liquida, se si sceglie come riferimento il sistema a concentrazione molare unitaria, l’attività
può essere espressa in funzione della concentrazione molare e
del coefficiente di attività gi della specie in esame, ai⫽giCi,
dove, ovviamente, per miscele ideali il coefficiente di attività
assume valore unitario e, conseguentemente, le attività si identificano con le concentrazioni. Per sistemi in fase gassosa, solitamente è più conveniente riferirsi al gas ideale a pressione
atmosferica, per cui ai⫽fi .
L’espressione più semplice della velocità di reazione che
rispetti i vincoli termodinamici e che si annulli all’equilibrio è:
1 NC νij  
− ∆G / RT
[17] rj = rj  1 −
∏ a  = rj 1 − e j
K j i =1 i 

dove con DGj si indica la variazione di energia libera di Gibbs
associata alla reazione, funzione sia della variazione di energia
[20]
− Ej / RT
kj = Aj e
dove Aj , Ej e R sono, rispettivamente, il fattore preesponenziale o di frequenza, l’energia di attivazione e la costante universale dei gas. L’espressione di Arrhenius indica chiaramente che la costante di velocità di reazione dipende in modo sensibile dalla temperatura e che tanto maggiore è il valore
dell’energia di attivazione tanto minore risulta quello di tale
costante. È importante sottolineare il significato fisico dell’energia di attivazione che, come illustrato in fig. 2, rappresenta la barriera energetica che deve essere superata dai reagenti affinché la reazione abbia corso. Facendo riferimento a
un semplice modello collisionale, solo gli urti tra le molecole reagenti che coinvolgano energie superiori all’energia di
attivazione sono efficaci nel produrne l’evoluzione desiderata. Le unità di misura della costante cinetica dipendono dalla
struttura della dipendenza dalla composizione del sistema,
cioè della funzione Yj (C).
)
coordinata
di reazione
ν
i =1
K j = ∏ ai ij
(
∆G j = ∆G °j + RT ln ∏ ai ij
E
tan
anz
ad
i le
gam
e
E
reagenti
DH
prodotti
coordinata di reazione
dis
dist
E
za
d
i le
gam
e
energia
reagenti
prodotti
fig. 2. Rappresentazione schematica dell’evoluzione energetica di un sistema reagente lungo la coordinata di reazione (a sinistra,
immagine tridimensionale che evidenzia la coordinata di reazione come il cammino di minor energia tra reagenti e prodotti).
266
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
Sviluppi teorici mostrano che, in realtà, l’espressione della
costante di velocità di reazione può essere più convenientemente espressa come
[21]
− Ej / RT
kj = BjT j e
m
dove l’esponente mj assume valori differenti in funzione dello
sviluppo teorico seguito, ma con valori sostanzialmente prossimi a 0,5. Dato che gli intervalli di temperatura considerati
non sono particolarmente estesi, questo effetto è modesto e
all’atto pratico giustifica l’impiego della più semplice relazione [20]. Qualora si evidenzino però deviazioni marcate dalla
linearità, tipiche della combinazione di due andamenti asintotici, ciò è quasi sicuramente indice della presenza di due reazioni tra loro competitive, prevalenti l’una sull’altra in funzione delle condizioni operative considerate.
La fig. 2 mostra anche un altro interessante aspetto. Come
già illustrato, nelle reazioni reversibili il valore della costante
cinetica della reazione inversa non è indipendente da quello
della reazione diretta, a causa della necessaria compatibilità
termodinamica. È facile ricavare dall’equazione [19] anche il
rapporto esistente tra le energie di attivazione delle due reazioni diretta e inversa, che coinvolge la variazione di entalpia
DHj associata alla reazione:
[22]
Ej = Ej − ∆H j
5.1.5 Sistemi complessi di reazioni
Generalmente si ha a che fare con reazioni coinvolgenti diversi passaggi, più o meno concatenati tra loro, nella trasformazione dei reagenti nei prodotti della reazione. In pratica, ogni
qualvolta siano presenti due o più reazioni, il sistema reagente
può essere definito complesso. Come già accennato, i tipi fondamentali di sistemi complessi contengono reazioni opposte,
reazioni parallele e reazioni consecutive. Tramite la combinazione di quest’ultime tipologie è possibile ricavare uno schema
complesso qualsivoglia. Si consideri quale esempio caratteristico una qualunque combustione di un idrocarburo, anche semplice quale il metano. Essa procede con meccanismo radicalico coinvolgente circa 20 specie chimiche connesse tra di loro
tramite 30 reazioni elementari. Inoltre, molte reazioni chimiche
danno luogo a sottoprodotti di reazione per cui è utile indicare
sinteticamente l’estensione della reazione relativamente a uno
dei reagenti più importanti, come pure la distribuzione relativa
dei prodotti di reazione. Per questo motivo, per lo studio di un
sistema reagente si fa spesso uso delle grandezze conversione
xi, resa hi, resa relativa hir e selettività Si, definite come segue:
[23]
ξi =
moli specie i-esima reagite
moli specie i--esima alimentate
invece relativamente al massimo numero di moli ottenibili per
quella data alimentazione del reagente. Si tratta quindi di chiarire sempre la definizione alla quale si fa riferimento. Con le
definizioni qui adottate, tutti i valori dei parametri di merito
risultano normalizzati nell’intervallo compreso tra 0 e 1. Per
comodità, nel seguito si farà riferimento sempre a grandezze
riferite alla quantità di materia (moli). In molti casi di interesse pratico è consuetudine riferirsi alla analoghe grandezze calcolate in base alla massa.
Per evidenziare gli andamenti tipici delle concentrazioni
delle specie coinvolte e dei parametri di merito per le tre tipologie base di reazioni complesse, si farà riferimento a un semplice reattore agitato discontinuo. Gli andamenti per reattori
continui agitati sono assolutamente analoghi e possono essere
ricavati seguendo la procedura indicata nel seguito.
Reazioni opposte
Un esempio permette di illustrare in modo semplice il comportamento di una reazione reversibile evidenziando ancora
una volta il legame esistente tra le costanti cinetiche della reazione diretta e inversa e la costante di equilibrio. Considerando, per semplicità, una reazione A⫺
⫺B, nella quale sia la reazione diretta sia quella inversa seguano una cinetica monomolecolare (r⫽k៬CA⫺kឈCB), le espressioni di bilancio materiale
in un reattore discontinuo perfettamente miscelato nel suo volume assumono la forma:
䉳
dCA
dC
= − B = − r = − kCA + kCB
dt
dt
avendo indicato con k៬ e kឈ le costanti cinetiche rispettivamente diretta e inversa. Assumendo il comportamento della miscela reagente ideale da un punto di vista termodinamico, un confronto con la [18] permette di stabilire che all’equilibrio il rapporto tra le due costanti cinetiche è uguale alla costante di
equilibrio termodinamico:
eq
k CB
[28] K = = eq
k CA
[27]
Le due equazioni [27] possono essere integrate analiticamente per ricavare l’andamento nel tempo delle due concentrazioni e conseguentemente della conversione del reagente A,
xA, definita dall’equazione [23]:
ξ eq
K +1 =
kt
[29] ln eq A
K
ξA − ξA
dove con xAeq⫽1Ⲑ(K⫹1) si è indicata la conversione in condizioni di equilibrio. L’equazione [29] mostra chiaramente che
per tempi di reazione che tendono all’infinito, la conversione
tende al valore di equilibrio.
Reazioni parallele
[24]
ηi =
moli specie i-esima prodotte
moli specie j-esima alimentate
[25]
ηir =
η
moli specie i-esima prodotte
= i
massime moli specie i-esima ottenibili ν i
[26]
Si =
ηi
moli specie i-esima prodotte
=
moli di tutte le specie prodotte NC
∑ηj
Per illustrare il comportamento di un sistema di reazioni parallele si può fare riferimento, per semplicità e senza
perdere di generalità, a due reazioni monomolecolari irreversibili A⫺ B e A⫺ C, le cui velocità di reazione sono, rispettivamente, r1⫽k1CA e r2⫽k2CA. Pertanto, le equazioni di bilancio materiale per le tre specie in un reattore discontinuo divengono:
䉴
䉴
[30]
dCA
= −( k1 + k2 )CA
dt
[31]
dCB
= k1CA
dt
j =1
Alternativamente, la resa può essere riferita alle moli della specie j-esima reagita anziché a quelle alimentate; hir è espressa
VOLUME V / STRUMENTI
䉴
267
CINETICA E CATALISI
1,0
conversione, resa e selettività
fig. 3. Andamento
dei parametri di merito
(conversione,
resa e selettività)
per una reazione con
meccanismo parallelo
(k1⫽0,1 s⫺1;
k2⫽0,5 s⫺1; CA0⫽1 mol/l;
CB0⫽CC0⫽0 mol/l).
conversione di A
0,9
0,8
resa in C
0,7
0,6
0,5
0,4
0,3
selettività B/(B⫹C)
0,2
0,1
0
resa in B
0
2
4
6
8
10
12
14
16
18
20
tempo (s)
[32]
dCC
= k2CA
dt
che possono essere facilmente integrate analiticamente supponendo inizialmente il reattore caricato con il solo reagente
A. Applicando le definizioni di conversione, resa e selettività
si ottengono le seguenti espressioni:
[33]
[34]
[35]
[36]
[37]
dC A
= − k1C A
dt
[38]
dC B
= k1C A − k2C B
dt
[39]
dCC
= k2C B
dt
ξA = 1− e− ( k1 + k2 )t
k1
k1 + k2
k
ηC = 1− e− ( k1 + k2 )t  2
k1 + k2
k
SB/( B+C ) = 1
k1 + k2
Tale sistema può essere integrato analiticamente supponendo, per esempio, il reattore alimentato inizialmente col solo
reagente A. Introducendo le concentrazioni così ricavate nelle
espressioni dei parametri di merito si ottiene
ηB = 1− e− ( k1 + k2 )t 
Da queste relazioni, i cui andamenti sono riportati in
fig. 3, si vede che sia la conversione sia le rese tendono al loro
valore massimo teorico al crescere del tempo di reazione. Ciò
non è vero per la selettività, che si mantiene costante durante
la reazione.
Reazioni in serie
Anche in questo caso, si possono analizzare gli andamenti nel tempo dei parametri di merito facendo riferimento a un
sistema A⫺ B e B⫺ C, le cui reazioni seguano una cinetica
del prim’ordine irreversibile, rispettivamente r1⫽k1CA e
r2⫽k2CB. I bilanci materiali delle tre specie coinvolte nella reazione divengono:
䉴
dei parametri di merito
(conversione,
resa e selettività)
per una reazione
con meccanismo
in serie (k1⫽0,1 s⫺1;
k2⫽0,5 s⫺1; CA0⫽1 mol/l,
CB0⫽CC0⫽0 mol/l).
0,9
conversione, resa e selettività
1,0
ξA = 1− e− k1t
[41]
ηB =
[42]
ηC = 1+
[43]
S B /( B + C ) =
(
k1
e− k1t − e− k2 t
k2 − k1
)
k1e− k2t k2 e− k1t
−
k2 − k1 k2 − k1
e
− k1t
1 + k1e
−e
− k1t
− k2 t
+ k2 e
− k1t
Dalle relazioni precedenti (i cui diagrammi sono riportati in fig. 4), si osserva che esiste un massimo per la resa di B.
La sua localizzazione temporale e il suo valore possono essere determinati imponendo le condizioni di estremo relativo
(dhBⲐdt⫽0):
䉴
fig. 4. Andamento
[40]
selettività B/(B⫹C)
0,8
0,7
resa in C
0,6
0,5
conversione di A
0,4
0,3
resa in B
0,2
0,1
0
0
5
10
15
20
25
30
35
40
45
50
tempo (s)
268
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
1,0
fig. 5. Andamento
0,9
concentrazione (mol/l)
delle concentrazioni
dei reagenti
per una reazione
con meccanismo
in serie (CA0⫽1 mol/l;
CB0⫽CC0⫽0 mol/l;
A, k1⫽0,1 s⫺1, k2⫽0,2 s⫺1;
B, k1⫽0,1 s⫺1, k2⫽0,5 s⫺1;
C, k1⫽0,1 s⫺1, k2⫽1 s⫺1).
A
0,8
CA
0,7
CC
0,6
0,5
0,4
0,3
CB
0,2
0,1
0
0
2
4
6
8
10
12
14
16
18
20
tempo (s)
1,0
concentrazione (mol/l)
0,9
CC
0,8
B
CA
0,7
0,6
0,5
0,4
0,3
0,2
CB
0,1
0
0
2
4
6
8
10
12
14
16
18
20
tempo (s)
1,0
concentrazione (mol/l)
0,9
CC
0,8
C
CA
0,7
0,6
0,5
0,4
0,3
0,2
CB
0,1
0
0
2
4
6
8
10
12
14
16
18
20
tempo (s)
[44]
t max =
[45]
η
ln( k2 / k1 )
k2 − k1
k2
max
B
 k  k2 − k1
= 1
 k2 
La selettività di B rispetto a C risulta invece massima al
tempo iniziale, ossia quando C è nullo. All’aumentare del tempo
di reazione tale valore risulta poi sempre decrescente (v. ancora fig. 4). Da quanto sopra riportato, si osserva che il tempo di
reazione che massimizza la resa in B non è lo stesso che massimizza la selettività di B rispetto a C. Pertanto nella gestione dei processi che avvengono con meccanismo in serie, è
importante aver ben chiaro qual è il parametro più importante
VOLUME V / STRUMENTI
da controllare, tra conversione (massima per t⫺⬁), resa di un
intermedio (massima per un tempo caratteristico) e selettività
(massima per t⫽0).
䉴
5.1.6 Metodi di semplificazione
di schemi cinetici complessi
Nella trattazione di schemi cinetici complessi, sovente è
opportuno ricorrere a semplificazioni che permettono di
derivare una legge cinetica globale mediante un’unica
espressione matematica, sia pure complessa. Ciò consente per esempio di evidenziare la cinetica della reazione
globale solo in funzione delle specie chimiche principali,
269
CINETICA E CATALISI
omettendo specie intermedie o particolarmente reattive.
Nella pratica si ricorre a due approssimazioni: quella dell’intermedio stazionario e quella dello stadio lento. La prima
si applica quando nello schema cinetico siano presenti specie particolarmente reattive e quindi in piccole quantità, tali
da poter essere in prima approssimazione trascurabili; la
seconda si applica invece quando la concentrazione delle
specie intermedie è elevata e quindi la loro presenza non
può essere trascurata.
ottenuta imponendo che dCB Ⲑdt⫽0. Ciò equivale ad assumere che la concentrazione di B, ossia della specie intermedia,
si mantenga stazionaria nell’intero processo o, più precisamente, che la velocità di formazione della specie equivalga a
quella della sua scomparsa: RB⫽0. Questo risultato, ottenuto
da un punto di vista meramente matematico, è una diretta conseguenza dell’elevata reattività della specie intermedia. L’unione di questi due fatti, ossia la ‘stazionarietà’ e l’applicazione dell’approssimazione a una specie intermedia, dà origine al nome di questa procedura di approssimazione. In realtà
l’andamento della concentrazione della specie B non è stazionario ma segue parallelamente quello della specie A. Il
limite dell’approssimazione, come evidenziato dalla fig. 6, si
manifesta negli istanti iniziali, poiché successivamente l’andamento della concentrazione ottenuto con l’approssimazione è molto prossimo a quello esatto. Pertanto, questa approssimazione è quanto più lecita, tanto più è alta la reattività della
specie considerata. Un esempio di applicazione classico è
quello delle reazioni a catena di tipo radicalico, quali quelle
di polimerizzazione o quelle di clorurazione omogenea di idrocarburi gassosi.
Approssimazione dell’intermedio stazionario
Per illustrare questo procedimento è utile fare riferimento
a un sistema semplice e fornire i criteri per una sua applicazione generale. Pertanto si consideri lo schema di due reazioni in serie, A⫺ B e B⫺ C, che seguono una cinetica irreversibile del primo ordine, analogamente a quanto sviluppato in
precedenza. Assumendo che inizialmente sia presente il solo
reagente A, l’integrazione analitica delle equazioni di bilancio
[37-39] fornisce:
[46] CA = CA0 e− k1t
䉴
[47]
CB = CA0
䉴
k1 ( e− k1t − e− k2 t
k2 − k1
k1CA − k2CB = 0
[52]
)
 k e− k2t k2 e− k1t 
CC = CA0  1+ 1
−
 k2 − k1 k2 − k1 
dove con C 0 si intende la concentrazione alle condizioni iniziali.
Come illustrato in fig. 5, all’aumentare del rapporto delle
costanti cinetiche delle due reazioni k2 Ⲑk1 l’andamento delle
concentrazioni in funzione del tempo è qualitativamente lo
stesso (in particolare la concentrazione di B presenta sempre un massimo), ma il massimo della concentrazione di B
diviene sempre meno pronunciato e si sposta sempre di più
verso l’origine dei tempi. Al limite, per k2/k1⬎⬎1 le equazioni [46-48] possono essere approssimate dalle seguenti
espressioni:
Approssimazione dello stadio lento
[48]
Un altro metodo di frequente applicazione nella semplificazione di schemi cinetici complessi è l’approssimazione dello
stadio lento. Essa si applica a processi reattivi che hanno luogo
attraverso una successione di stadi. A tal fine, si consideri un
sistema nel quale la trasformazione del reagente A nel prodotto
B avviene attraverso la specie intermedia X:
1
2
⫺

→X ←


→B
⫺
⫺
A⫺
⫺
⫺
⫺
⫺
←




[53]
䉴
䉳
䉴
䉳
Se si assume per semplicità che tutti gli stadi seguano
una cinetica del prim’ordine, la velocità di ognuno di essi
sarà espressa dalle seguenti relazioni, direttamente ricavate
dalla [17]:
[49]
CA = CA0 e− k1t
[54]
r1 = k1 ( CA − CX / K1 )
[50]
k
k
CB ≈ C 1 e− k1t = 1 CA
k2
k2
[55]
r2 = k2 ( CX − CB / K2 )
[51]
0
A
CC ≈ CA0 (1− e− k1t
)
Se il sistema è aperto e si trova in condizioni stazionarie,
la velocità di reazione di ognuno degli stadi coinvolti avrà lo
stesso valore (r⫽r1⫽r2), mentre la concentrazione di ogni
specie si manterrà inalterata nel tempo. Ne consegue che,
uguagliando le due equazioni precedenti è possibile ricavare
che corrispondono alla soluzione del sistema di equazioni [3739] dove sia stata sostituita all’equazione differenziale [38] l’equazione algebrica:
1
10⫺1
concentrazione (mol/l)
fig. 6. Visualizzazione
dell’errore insito
nell’approssimazione
dell’intermedio stazionario
(CA0⫽1 mol/l;
CB0⫽CC0⫽0 mol/l;
k1⫽0,1 s⫺1; k2⫽10 s⫺1).
CA
CC
CB
10⫺2
10⫺3
soluzione approssimata
10⫺4
soluzione non approssimata
10⫺5
10⫺6
0
2
4
6
8
10
12
14
16
18
20
tempo (s)
270
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
la concentrazione della specie intermedia che sostituita, per
esempio, nella [54] fornisce l’espressione della velocità del
processo globale:
k k C − C B / ( K1 K 2 ) 
[56]
r = r1 = r2 = 1 2  A
k2 + k1 / K1
Inoltre, il prodotto delle costanti di equilibrio dei singoli
stadi fornisce la costante di equilibrio globale della reazione
(K⫽K1K2). Se la costante cinetica del primo stadio è molto
maggiore di quella del secondo (k1⬎⬎k2) l’espressione [56]
diviene:
[57]
r ≈ k2 ( K1CA − CB / K2 )
per cui i reagenti A e X possono considerarsi in equilibrio virtuale e la velocità del processo è governata da quella del secondo stadio, che viene chiamato stadio lento in quanto la sua
costante di velocità è piccola. In pratica, l’espressione [57] può
essere ottenuta inserendo nell’ espressione della velocità di reazione del secondo stadio della [55], la concentrazione dell’intermedio X calcolata come se fosse in equilibrio con A, ossia
CX⫽K1CA. Se si verifica il caso opposto, ossia che lo stadio
lento del processo è il primo (k1⬍⬍k2), la [56] si riduce a:
[58]
r ≈ k1 C A − C B / ( K1 K 2 ) 
che potrebbe essere ottenuta sostituendo nella [54] la concentrazione dell’intermedio supposta all’equilibrio con il prodotto B della reazione, CX⫽CB ⲐK2.
Il concetto di stadio lento può essere quindi facilmente
generalizzato a un sistema che evolva attraverso un numero
generico di stadi di reazione. Se uno di essi presenta una costante di velocità di reazione molto inferiore agli altri, la velocità
del processo globale si può ricavare da essa (e lo stadio viene
identificato come lo stadio lento del processo), sostituendovi
le concentrazioni degli altri intermedi calcolate assumendo che
gli altri stadi siano all’equilibrio termodinamico. Questa approssimazione è molto utile per la riduzione di schemi cinetici complessi, soprattutto quando non sia facile ricavare la concentrazione delle specie intermedie. Occorre però precisare che essa
rappresenta unicamente un modo operativo di semplificazione: è infatti possibile sovente interpretare dati cinetici con accuratezze confrontabili mediante espressioni ricavate assumendo differenti ipotesi di stadio lento.
Questa approssimazione trova la sua più ampia applicazione nello studio della cinetica dei processi catalitici eterogenei, dove le espressioni più utilizzate della velocità di reazione sono per lo più ottenute con questo metodo.
5.1.7 Aspetti microfisici e molecolari
della velocità di reazione
La cinetica delle reazioni chimiche è stata sinora trattata da un
punto di vista macroscopico, senza entrare nel dettaglio delle
sue implicazioni microfisiche che verranno nel seguito approfondite sulla base della teoria collisionale e della teoria dello stato
di transizione. Sarà poi presa in esame l’influenza della pressione sulla costante cinetica, con particolare riferimento alle
reazioni monomolecolari.
Teoria collisionale
In cinetica chimica sono molto frequenti gli stadi elementari bimolecolari, quali per esempio le reazioni di sostituzione
e quelle di ricombinazione. Per effetto di una collisione ha
VOLUME V / STRUMENTI
luogo una redistribuzione dei legami tra le molecole coinvolte. La teoria collisionale si presta quindi particolarmente per
l’interpretazione delle reazioni bimolecolari, in quanto è basata sull’ipotesi che la reazione abbia luogo per effetto della collisione tra le due molecole e che siano efficaci ai fini della reazione solo quegli urti nei quali l’energia coinvolta sia superiore a un determinato valore di soglia. Per semplicità è conveniente
riferirsi a una reazione che abbia luogo in fase gassosa, anche
se i risultati ottenuti hanno poi validità generale. Per una reazione del tipo A⫹B⫺ prodotti, la velocità del processo risulta espressa dal prodotto tra il numero di collisioni nell’unità di
tempo e di volume Z(A,B) e la probabilità che la collisione dia
luogo alla reazione W(A,B):
䉴
[59]
r = Z ( A,B)W ( A,B)
Più semplicemente, il primo termine può essere calcolato
mediante la teoria cinetica dei gas, tramite la quale, assumendo urti elastici tra molecole sferiche rigide con diametro dA e
dB e massa mA e mB, in assenza di campi di forza esterni, si
ottiene:
[60]
Z ( A, B) = 2σ N A2
2 k BT
C C
πµ A B
dove NA e kB sono, rispettivamente, il numero di Avogadro e la
costante di Boltzmann, s⫽0,25p(dA⫹dB)2 è la sezione d’urto
geometrica corrispondente alla collisione delle due sfere rigide e infine m⫽mAmB Ⲑ(mA⫹mB ) è la massa ridotta delle due
molecole collidenti. Il termine di probabilità può essere valutato applicando la legge di distribuzione di Maxwell-Boltzmann come frazione di molecole aventi un’energia superiore
a un valore di soglia E:
[61]
W ( A,B) = e− E / RT
Sostituendo nella [59] si ottiene:
[62]
r = 2σ N A2
2 k BT − E / RT
e
C AC B = BT 0,5e− E / RT C AC B
πµ
L’espressione così ricavata spiega alcune evidenze sperimentali, quali la dipendenza della velocità di reazione dal
prodotto delle concentrazioni delle specie coinvolte e la dipendenza esponenziale della costante cinetica dalla temperatura. Il fattore di frequenza così calcolato mostra una dipendenza dalla radice quadrata della temperatura, anche se all’atto pratico, operando in un intervallo limitato di temperatura,
risulta difficile evidenziare tale dipendenza dall’analisi dei
semplici dati sperimentali. In conclusione, la teoria collisionale, pur nella più semplice delle sue formulazioni, fornisce
una interpretazione dei termini che caratterizzano la costante cinetica: la dipendenza dalla temperatura riflette la distribuzione dell’energia tra le diverse molecole, il fattore preesponenziale, invece, riflette la frequenza con la quale le molecole collidono.
In realtà, la sezione d’urto calcolata considerando le molecole quali sfere rigide costituisce un’approssimazione alquanto rozza e i fattori di frequenza così calcolati differiscono di
qualche ordine di grandezza da quelli sperimentali. Per correggere ciò è necessario rimuovere l’ipotesi di sfericità e considerare l’orientamento reciproco delle molecole nell’urto. Inoltre
bisogna considerare la presenza delle forze di interazione esistenti tra le due molecole già in fase di avvicinamento. Di conseguenza, la sezione d’urto diviene essa stessa una funzione dell’energia della collisione e pertanto l’espressione della velocità
di reazione può essere generalizzata, moltiplicando la frazione
271
CINETICA E CATALISI
di coppie molecolari aventi un’energia e per il corrispondente
valore della sezione d’urto e per il valore della loro velocità
relativa e poi integrando l’espressione così ricavata per tutti i
valori di energia. Si ottiene così la seguente espressione:
1,5
N C C  2  ∞
− ε / k BT
[63]
dε
r= A A B
 ∫ εσ (ε )e
k
T
πµ  B  0
la cui integrazione dipende dall’andamento della sezione d’urto con l’energia della collisione.
L’analisi precedente mostra chiaramente che la stima della
costante cinetica passa attraverso il calcolo delle interazioni
esistenti tra le molecole collidenti. È importante sottolineare
che il parametro critico è rappresentato dal valore della sezione d’urto in funzione dell’energia della collisione. I valori della
sezione d’urto possono essere ricavati sperimentalmente mediante collisione di fasci molecolari o stimati per via teorica. Oggi
questi calcoli possono essere effettuati con l’ausilio di software basati sulla meccanica quantistica (v. par. 5.1.10).
Teoria dello stato di transizione
La teoria collisionale permette di effettuare il calcolo della
costante cinetica solo attraverso uno studio della dinamica delle
collisioni tra le molecole reagenti. Ciò comporta l’esecuzione
di calcoli molto laboriosi, a meno che non si disponga di misure sperimentali della sezione d’urto in funzione dell’energia
delle molecole collidenti. È allora opportuno poter disporre di
un metodo approssimato che consenta di aggirare, almeno in
prima approssimazione, tale ostacolo.
Il significato dello stato di transizione o complesso attivato, indicato solitamente come X⬆, può essere illustrato esaminando la fig. 7, che rappresenta l’evoluzione di un sistema reagente lungo la coordinata di reazione (ossia il cammino di minor
energia che connette i reagenti con i prodotti). Il massimo di
tale curva viene chiamato stato di transizione e rappresenta una
configurazione di sistema all’incirca equidistante tra quella dei
prodotti e quella dei reagenti. Secondo la teoria dello stato di
transizione la reazione bimolecolare può essere scissa in due
stadi: il primo corrisponde alla formazione del complesso attivato e il secondo, più lento, alla sua decomposizione:
[64]
≠
A + B⫺
⫺X
[65]
X≠ ⫺
⫺➤ prodotti
䉳
䉴
䉴
Pertanto applicando l’approssimazione dell’intermedio stazionario (v. par. 5.1.6), la velocità del processo risulta espressa da:
energia
A⫹B
reagenti
M⫹N
prodotti
fig. 7. Andamento energetico di una reazione
con illustrazione dello stato di transizione.
272
r = k ≠ C X ≠ = k ≠ K ≠ C AC B
dove k⬆ e K⬆ indicano, rispettivamente, la costante cinetica
della reazione di decomposizione del complesso attivato e la
costante di equilibrio del suo processo di formazione. La prima
può essere calcolata con i metodi della meccanica statistica,
mediante i quali si dimostra che essa è indipendente dalla natura della reazione in esame ma dipende unicamente dalla temperatura e da due costanti universali, quella di Planck, h, e quella di Boltzmann, kB:
kT
[67] k ≠ = B
h
La costante di equilibrio può essere valutata dalla variazione di energia libera standard DG⬆ associata alla formazione del complesso attivato a partire dai reagenti:
[68]
K ≠ = e− ∆G
≠
/ RT
= e− ( ∆H
≠
−T ∆S ≠ )/ RT
Pertanto, sostituendo la [67] e la [68] nella [66] e confrontando il risultato così trovato con l’espressione di Arrhenius, ne consegue che l’energia di attivazione della reazione
dipende dalla variazione di entalpia associata alla formazione
del complesso attivato:
[69]
E = ∆H ≠ + RT
e che il fattore di frequenza dipende dall’entropia di formazione del complesso attivato, che fisicamente esprime la probabilità che esso si formi
≠
kT
[70] A = B e(1+ ∆S / R )
h
DH ⬆e DS ⬆ sono spesso indicati come entalpia ed entropia di
attivazione. I loro valori possono essere stimati dalle proprietà
del complesso attivato mediante i metodi della meccanica statistica, ricorrendo alla sua configurazione geometrica, alle sue
frequenze di vibrazione e alle energie dei legami coinvolti.
Prima dell’avvento delle attuali generazioni di computer che
hanno reso possibile la stima di queste grandezze con i metodi della meccanica quantistica a partire dai principi primi, queste stime venivano effettuate, e sovente lo sono tuttora, ricorrendo ai cosiddetti metodi dei contributi di gruppo, che assegnano a ciascuna porzione della molecola valori specifici di
entalpia e di entropia di formazione, definiti in modo che le
proprietà della molecola finale, o in questo caso del complesso attivato, siano fornite dalla somma dei contributi specifici
di ciascun gruppo in essa presente. A titolo di esempio, conoscendo i valori di entalpia di formazione associati ai gruppi
CH2 e CH3 è possibile stimare le entalpie di formazione di tutti
gli alcani lineari.
Reazioni monomolecolari e dipendenza dalla pressione
della costante cinetica
X⬆
coordinata di reazione
[66]
La dipendenza delle costanti cinetiche dalla pressione è
così piccola che per osservarla è necessario considerare sistemi che operino a qualche centinaio di bar se non un migliaio,
dato che questa dipendenza coinvolge la variazione di volume
molare, DV*, tra il reagente nel suo stato attivato e in quello
normale. Derivando infatti l’espressione della costante di velocità di reazione ottenuta dalla teoria dello stato di transizione
rispetto alla pressione è possibile dimostrare che
[71]
∆V *
 ∂ ln k 
 =−

RT
∂P  T
Pertanto, se il complesso attivato ha un volume maggiore
della molecola nel suo stato normale, un aumento di pressione
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
provoca una diminuzione della costante cinetica. Essendo però
questa variazione piccola, si spiega il modesto effetto della
pressione sulla costante di velocità, tanto che solitamente esso
non viene considerato.
Nelle reazioni monomolecolari in fase gassosa l’effetto
della pressione può però essere assai evidente. Le reazioni
monomolecolari coinvolgono la trasformazione di un’unica
specie nei prodotti di reazione. Esempi tipici sono le reazioni
di isomerizzazione e quelle di decomposizione termica. La
cinetica di questi processi presenta un comportamento peculiare che può essere interpretato sulla base della trattazione sviluppata per la prima volta da Lindeman. Affinché una molecola possa dar luogo a una reazione, essa dovrà essere eccitata a un livello di energia superiore a quello fondamentale; in
altre parole dovrà essere attivata. In fase gassosa, l’attivazione ha luogo attraverso le collisioni con le altre molecole presenti nel sistema e genericamente indicate con il nome di terzo
corpo, qui indicato con M. Successivamente, la molecola attivata A* si trasforma nei prodotti:
[72]
A+ M⫺
⫺ A* + M
[73]
A *⫺
⫺➤ prodotti
䉳
−1
 1
1
r = F (T , ka0 , ka∞)  ∞ + 0  C A
 ka ka 
dalla quale è chiaro che F⫽1 nella trattazione di Lindeman.
Affinché la trattazione usata attualmente possa consentire
la stima della costante cinetica è necessario valutare teoricamente la costante di velocità del processo di eccitazione di una
molecola. Tale processo dipenderà dai gradi di libertà presenti nella molecola (traslazionali, rotazionali e vibrazionali) e dal
modo in cui l’energia ricevuta negli urti si ridistribuisce tra i
vari livelli energetici associati a tali gradi di libertà. A questo
fine sono state proposte diverse teorie, tra le quali è importante
citare quella sviluppata da Rice, Ramsperger, Kassel e Markus
(indicata come RRKM) e la sua modificazione quantistica, la
cui trattazione è però rimandata ai testi specializzati. Oggi,
naturalmente, si può fare uso di metodi matematici che consentono tale stima in modo non eccessivamente oneroso.
[77]
䉴
䉴
Per valutare la velocità di reazione globale si può ricorrere all’approssimazione dell’intermedio stazionario, applicata alla specie attivata (sicuramente molto reattiva) per stimarne la concentrazione, e successivamente sostituire quest’ultima nell’espressione della velocità del secondo stadio
della reazione (decomposizione della specie attivata). Supponendo che tutti gli atti cinetici siano elementari, è facile
ricavare che:
−1
 k1
k1C AC M
1 
= + C A = kaC A
[74] r = k2C A* = k2 k1C M + k2  k2 k1 k1C M 
Si può osservare che la costante apparente di pseudoprim’ordine ka presenta due andamenti asintotici. Per alti valori della concentrazione del terzo corpo, equivalenti a sistemi
ad alta pressione, la costante apparente si identifica con una
combinazione delle sole costanti cinetiche e la reazione si manifesta come una reazione del prim’ordine rispetto al reagente
principale:
k
[75] ka∞ ≈ 1 k2
k1
A basse concentrazioni del terzo corpo, ossia a basse pressioni, si manifesta una dipendenza dalla concentrazione di quest’ultimo e quindi la reazione globalmente appare del secondo ordine, dipendendo sia dalla concentrazione del reagente
sia da quella del terzo corpo:
[76] ka0 ≈ k1C M
L’insorgenza della dipendenza dalla pressione della costante cinetica di pseudoprim’ordine si presenta per un valore ben
definito di pressione che ovviamente dipende dal sistema reagente considerato. Questo valore viene indicato come P1Ⲑ2 e
indica quella pressione alla quale la costante cinetica assume
un valore corrispondente alla metà del valore asintotico di alta
pressione. La regione delle pressioni inferiori a P1Ⲑ2 viene chiamata regione di falloff. La trattazione di Lindeman ha il pregio della semplicità. Oggi però i due andamenti asintotici di
alta e bassa pressione sono interpolati tramite correlazioni più
complesse, quali quella di Troe, nella quale la [74] viene modificata introducendo una dipendenza da un fattore F funzione
VOLUME V / STRUMENTI
della temperatura e dei parametri delle due costanti asintotiche; si ha F⫽Fcent(T )1ⲐP, con P⫽f(k 0a,ka⬁,CM ,Fcent):
5.1.8 Cinetica delle reazioni in soluzione
In fase liquida, la frequenza delle collisioni tra i reagenti è più
elevata che in fase gassosa, data la loro maggior concentrazione. Queste reazioni vengono spesso condotte in soluzione
con un opportuno solvente che può a sua volta interagire con
le molecole reagenti. Un esempio classico è rappresentato dall’acqua che, a causa della sua costante dielettrica, è in grado
di dissociare gli elettroliti nei loro ioni costituenti, che sono i
reali reagenti della reazione. In genere, un solvente può esercitare la sua azione anche coordinandosi con i reagenti o con
un intermedio di reazione. In questo caso l’azione del solvente è tale da ridurre la reattività della specie coinvolta.
In termini generali, in una reazione condotta in soluzione,
la maggior parte delle collisioni avviene con le molecole del
solvente; si tratta quindi di collisioni non reattive, ma che
comunque agevolano la formazione del complesso attivato. Per
la stima della costante cinetica è quindi possibile applicare la
teoria dello stato di transizione; in questo caso è però necessario considerare la possibile non idealità della soluzione e
quindi ricorrere alle attività anziché alle concentrazioni. Pertanto la costante di equilibrio di formazione del complesso attivato, in un percorso di reazione come quello delle equazioni
[64] e [65], sarà data da
[78]
K≠ =
aX ≠
a A aB
=
γ X≠
CX ≠
γ Aγ B C AC B
e quindi, sostituendo questa espressione nella [66], la costante di velocità della reazione globale risulterà:
[79]
k=
k BT ≠ γ Aγ B
γ γ
K
= k id A B
h
γ X≠
γ X≠
dove kid indica il valore della costante nelle condizioni di soluzione ideale. L’equazione [79] mostra quindi che il ruolo della
non idealità della soluzione è estremamente importante in quanto, a causa delle forti dipendenze di tipo non lineare dei coefficienti di attività dalla composizione, le deviazioni dal valore
kid possono essere estremamente marcate. Ciò è particolarmente
vero in sistemi contenenti elettroliti, che favoriscono comportamenti non ideali anche se sono presenti in piccole concentrazioni. L’equazione [79] permette inoltre di studiare la dipendenza della costante cinetica dal tipo di solvente impiegato, in
273
CINETICA E CATALISI
quanto la sua influenza si manifesta essenzialmente sui valori
dei coefficienti di attività poiché essi riflettono le interazioni
chimiche e fisiche tra le molecole presenti.
5.1.9 Cinetica delle reazioni eterogenee
Nella pratica, è frequente il caso di reagenti appartenenti a fasi
diverse, le quali debbono quindi essere messe in stretto contatto affinché la reazione possa procedere agevolmente. È consueto inoltre il caso che nel sistema sia presente un’opportuna
superficie solida le cui proprietà siano tali da interagire con le
specie reagenti, in modo da aumentare la velocità della reazione. La trattazione della cinetica dei processi reattivi eterogenei presenta pertanto delle peculiarità rispetto a quanto esaminato sinora per i sistemi omogenei. Nei sistemi eterogenei
sono infatti presenti fenomeni di trasporto di materia tra le fasi
nonché fenomeni di interazione chimico-fisica tra le superfici solide e i reagenti presenti in fase fluida. Queste interazioni sono di importanza rilevante poiché sono in grado di condizionare considerevolmente l’evoluzione nel tempo della reazione. In particolare, saranno qui esaminate la trattazione della
cinetica dei processi catalitici eterogenei, quella delle reazioni fra un gas e un liquido e infine quella delle reazioni non
catalitiche tra un gas e un solido.
Reazioni catalitiche
Vi sono reazioni estremamente lente se condotte in fase
omogenea che diventano però rapide se i reagenti sono posti a
contatto con una opportuna superficie solida che agisce da catalizzatore. Storicamente, il primo esempio di catalisi risale agli
studi sulla deidrogenazione degli alcoli condotti da Martin van
Marum nel 1796. Esempi di combustione catalitica furono poi
realizzati nel 1817 da Humphry Davy e Johann Wolfgang Döbereiner. Nel 1825 Michael Faraday fu il primo a studiare la reazione di combustione catalitica tra idrogeno e ossigeno. Il termine catalisi fu introdotto da Jöns Jacob Berzelius nel 1836
sulla base delle osservazioni sulla decomposizione dell’ammoniaca in contatto con i metalli, mutuandolo dal greco kat¥lusij
«scioglimento». Oggi, in termini rigorosi, si definisce catalizzatore una sostanza che aumenta la velocità di raggiungimento
dell’equilibrio in un sistema reagente, senza comparire nei prodotti di reazione e senza modificare i fattori termodinamici
intrinseci del sistema stesso. Pertanto un catalizzatore non interviene nel bilancio materiale del sistema reagente, in quanto non
si produce né si consuma per effetto della reazione. Inoltre, non
modificando la termodinamica del sistema, non è mai in grado
di far avvenire una reazione termodinamicamente impossibile.
Oggi la catalisi riveste un ruolo fondamentale in tutti i processi chimici industriali, dato che oltre il 90% delle specie prodotte industrialmente coinvolge un processo catalitico.
Per illustrare il comportamento di un catalizzatore è utile
far riferimento a una reazione generica:
[80]
A + B⫺
⫺M + N
䉳
䉴
Al sistema si aggiunge un’opportuna sostanza C che, per
esempio, sia in grado di interagire chimicamente con uno dei
due reagenti, in modo che la reazione possa procedere per stadi,
e sia ripristinata tal quale alla fine della reazione:
274
[81]
A + C⫺
⫺X
[82]
X + B⫺
⫺ M+ N+ C
䉳
䉳
䉴
䉴
La sostanza C, caratterizzata dal comportamento così
descritto, è chiamata catalizzatore. Da un punto di vista chimico-fisico il suo intervento nel processo provoca un’alterazione dell’andamento energetico della reazione: mentre i punti
iniziale e finale rimangono inalterati, la reazione procede seguendo un diverso cammino rispetto al processo condotto in assenza di catalizzatore. Questo cammino prevede la presenza di un
minimo di energia in corrispondenza della formazione del prodotto di interazione X tra catalizzatore e reagente.
In termini generali, il catalizzatore può essere presente nella
stessa fase dei reagenti, e in tal caso si parla di catalisi omogenea, oppure in una fase diversa, nel qual caso si parla di catalisi eterogenea. Esempi di catalisi omogenea sono rappresentati dalla catalisi acido-base (nel senso di Brönsted-Lowry), da
quella coinvolgente composti organometallici o da quella basata sull’aggiunta di sostanze chelanti in grado di solubilizzare
opportuni metalli. Relativamente alla catalisi eterogenea, il cui
uso è preferito nelle applicazioni industriali per la facilità di
recupero del catalizzatore a fine reazione, esempi classici sono
la catalisi metallica (a base di polveri, filamenti o film metallici supportati su particelle porose) e quella coinvolgente ossidi metallici o sistemi acido-base (tipicamente acidi di Lewis).
Poiché la trattazione della catalisi omogenea non presenta
particolarità rispetto a quanto sinora esaminato, in quanto basta
introdurre nelle espressioni della velocità di reazione la concentrazione del catalizzatore, nel seguito l’attenzione sarà focalizzata solo sui processi catalitici eterogenei. In essi, l’azione
catalitica è indotta dall’interazione, generalmente di natura chimica, tra la superficie del catalizzatore solido e i reagenti contenuti nella fase fluida. Risulta quindi evidente che l’azione
catalitica di una superficie dipende dalla sua capacità di adsorbire i reagenti.
Una reazione catalitica eterogenea è un classico processo
che avviene mediante una serie di stadi: a) diffusione dei reagenti dalla fase fluida alla superficie del catalizzatore; b) adsorbimento dei reagenti sulla superficie; c) reazione chimica superficiale; d ) desorbimento dei prodotti dalla superficie; e) diffusione dei prodotti dalla superficie alla fase fluida.
Sono pertanto presenti sia stadi di natura fisica (il primo e
l’ultimo) sia stadi di natura chimica (i tre intermedi). Se il catalizzatore è realizzato disperdendo l’elemento attivo sulla superficie che si sviluppa all’interno di una particella porosa, i processi diffusionali possono essere ulteriormente suddivisi in diffusione esterna (il trasporto di materia tra il cuore della fase
fluida e la superficie esterna della particella) e diffusione interna (il trasporto di materia nei pori della particella catalitica).
Gli stadi citati sono consecutivi e se uno di loro è molto più
lento degli altri determinerà la velocità del processo globale.
Solo nel caso in cui gli stadi di natura chimica siano particolarmente rapidi, lo stadio lento coincide con uno degli stadi di
natura diffusionale. Solitamente questi ultimi sono più rapidi
e lo stadio lento del processo coincide spesso con uno di natura chimica.
In termini generali, la trattazione di un sistema che coinvolge un così elevato numero di stadi presenta alcune complessità matematiche. Pertanto, per ottenere espressioni della
velocità di reazione in forma chiusa si fa generalmente uso dei
metodi di semplificazione degli schemi cinetici complessi
descritti in precedenza, quali l’approssimazione dello stadio
lento e quella dell’intermedio stazionario. Prima di procedere, è opportuno fare una precisazione. Se l’individuazione dello
stadio lento del processo è basata su informazioni chimicofisiche quali l’abbondanza relativa delle specie intermedie o i
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
rapporti di velocità di reazione, è possibile ottenere da dati
puramente cinetici, ossia dall’espressione della velocità di reazione, informazioni sul meccanismo di reazione. In assenza di
tali indicazioni, questo procedimento non è lecito e quindi non
esiste alcun nesso fisico tra l’espressione matematica della
velocità di reazione e il reale meccanismo della stessa. È infatti frequente il caso in cui differenti espressioni cinetiche, ricavate sulla base di diversi stadi lenti della reazione, siano in
grado di interpretare gli andamenti sperimentali con accuratezza comparabile. In questo caso, la discriminazione tra i diversi possibili meccanismi richiede informazioni sperimentali di
tipo chimico-fisico, quali l’energia di attivazione di un processo di desorbimento, o il rispetto del vincolo di energia di
attivazione positiva, o il fatto che siano in gioco valori dei fattori di frequenza inferiori a quelli determinati mediante la teoria collisionale, dato che essi rappresentano un massimo teorico. È da sottolineare che la scelta di un’espressione cinetica
che rispetti il reale meccanismo della reazione consente poi
delle ragionevoli estrapolazioni anche al di fuori del semplice
intervallo di parametri di temperatura, pressione e concentrazione impiegato per la stima dei parametri.
Schema cinetico di Langmuir-Hinshelwood
Si fa riferimento specificatamente agli stadi chimici considerando una generica reazione chimica reversibile come la
[81]. In prima ipotesi, è possibile ritenere che tutte le specie
coinvolte si adsorbano sulla superficie, occupando ciascuna un
sito della superficie catalitica. Tale adsorbimento, che descrive le interazioni di tipo chimico tra reagenti e superfici, viene
detto di Langmuir, e la sua velocità è fornita dalla seguente
espressione:
[83] riad = kiad Ciϑv − kiadϑi i = A, B, M, N
dove con ÿi e ÿv sono state indicate, rispettivamente, la frazione di siti superficiali occupati dalla specie i-esima (ossia A,
B, M o N nell’esempio in esame) e la frazione di siti liberi.
Ovviamente deve verificarsi la conservazione dei siti superficiali, espressa dalla relazione seguente:
[84]
1= ϑv + ∑ i ϑi
È ragionevole ritenere che la reazione superficiale coinvolga le specie adsorbite sulla superficie, per cui:

ϑ ϑ 
rs = ks  ϑ Aϑ B − M N 
Ks 

Se si assume che lo stadio lento coincida con la reazione
superficiale, è possibile supporre che tutti gli stadi di adsorbimento e desorbimento siano in condizioni prossime a quelle
di equilibrio (ossia riad ⬇0). Risulta così possibile ricavare dalla
[83] la frazione di siti occupati in funzione delle concentrazioni in fase fluida e della frazione dei siti liberi:
kiad
[86] ϑi = ad Ciϑv = bC
i iϑv
ki
[85]
Sostituendo queste espressioni nella [84] è possibile ricavare anche la ÿv. Infine, sostituendo nella [85] le espressioni
dei siti liberi e di quelli occupati dalle singole specie adsorbite si ricava l’espressione della velocità di reazione:
[87]
r = rs =

C C 
ks bAbBC AC B  1 − M N 
KC AC B 

(1 + b C
A
VOLUME V / STRUMENTI
A
+ bBC B + bM C M + bN C N
)
2
dove la costante di equilibrio K è riferita alla reazione globale poiché:
[88]
Ks = K
bM bN
bAbB
Dalla [87] si vede che è possibile giustificare teoricamente espressioni razionali della velocità di reazione e conseguentemente ordini di reazione frazionari o negativi in espressioni cinetiche tipo legge di potenza. Si vede inoltre che nel
fenomeno di adsorbimento tutte le specie competono, in base
al valore della loro costante di equilibrio di adsorbimento, nel
ricoprimento dei siti superficiali disponibili.
Ovviamente l’espressione precedentemente ricavata dipende sia dalla scelta effettuata sullo stadio lento della reazione
sia dall’espressione considerata per il processo di adsorbimento.
Se per esempio si fosse assunto quale stadio lento del processo l’adsorbimento del reagente A, applicando la procedura illustrata si sarebbe ottenuta le seguente espressione cinetica:
[89]
r≈
(
k AC AC B 1 − C M C N KC AC B
)
1 + bA (C A K ) + bBC B + bM C M + bN C N
Inoltre, esistono espressioni alternative alla semplice espressione di Langmuir con adsorbimento su di un singolo sito superficiale [83]. Per esempio, possono essere considerati processi
di adsorbimento nei quali intervengono due siti superficiali,
coinvolgendo o meno un processo dissociativo
[90]
ad
A + 2σ ⫺
⫺A
[91]
ad
ad
AB + 2σ ⫺
⫺A + B
䉳
䉴
䉳
䉴
la cui velocità risulta essere, rispettivamente:
[92]
rAad = k Aad C Aϑ v2 − k Aadϑ A
ad
ad
ad
[93]
rAB
= k AB
C ABϑ v2 − k AB
ϑ Aϑ B
In questi casi si parla di meccanismi cinetici di tipo dualsite. Esistono anche importanti esempi di processi che seguono l’isoterma di adsorbimento tipo Elövich-Temking, dove la
dipendenza dai siti superficiali occupati dalla specie è di tipo
esponenziale
−hϑ
−g ϑ
[94]
ri ad = kiad C Ae i i − kiad e i i
Un tipico esempio è costituito dal processo di adsorbimento di azoto su ferro nei processi di sintesi dell’ammoniaca (N2⫹3H2⫺
⫺2NH3). In questo specifico caso, impiegando
la [94] per l’adsorbimento di azoto e ipotizzando quest’ultimo quale stadio lento, è facile ricavare la seguente espressione della cinetica di reazione, la cui validità è stata verificata
ampiamente mediante un uso intensivo nella progettazione dei
reattori
α
2
 CH3  
1 C NH3 
ad
2
[95]
r = r = k1CN  2   1 −

2 
K C N C H3 
 CN 2  
2
2
dove k1⫽k៬Nad2(kឈNad2k Ⲑk៬Nad2 )a e a⫽gN2Ⲑ(gN2⫹hN2). La [95] è nota sotto
il nome di cinetica di Temking-Pyzev e in essa il valore di a è
compreso tra 0,5 e 0,65. Dato che i reagenti sono impiegati in
fase gassosa e il processo è condotto ad alte pressioni, solitamente nell’espressione [95] si ricorre all’impiego delle fugacità anziché delle concentrazioni per tener conto delle non idealità del comportamento del gas.
Un caso ulteriore è quello in cui la reazione coinvolga sia
una specie adsorbita sul catalizzatore sia una ancora in fase
fluida. Si parla allora di meccanismi tipo Eley-Rideal:
䉳
䉴
275
CINETICA E CATALISI
[96]
Aad + B⫺
⫺➤ M + N
䉴
per i quali, assumendo come stadio lento la reazione superficiale,
[97]
rs = ksϑ AC B
è immediato ricavare la seguente espressione cinetica, dove il
denominatore contiene solo i contributi delle specie che si
adsorbono sul catalizzatore (nel caso specifico non esiste specie B adsorbita):
[98]
r ≈ rs =
ks bAC AC B
1 + bAC A + bM C M + bN C N
[100] Ci ( x ) =
Efficienza dei catalizzatori
La velocità di una reazione catalitica è influenzata, oltre
che dalla natura chimica della reazione, anche da fenomeni
fisici di trasporto di materia e di calore. Infatti i componenti
della miscela fluida, prima di reagire, debbono diffondere dal
cuore della miscela alla superficie della particella e poi all’interno della stessa tramite la rete di pori presente. Il cammino
inverso deve essere poi percorso dai prodotti della reazione. A
causa dei processi diffusivi intraparticellari e del conseguente
consumo dei reagenti dovuto alla reazione chimica, all’interno della particella si instaura un profilo di concentrazione il
cui valor medio può differire anche notevolmente da quello
esistente in corrispondenza della sua superficie. Una descrizione di tale profilo può essere ottenuta integrando l’equazione di bilancio materiale all’interno della particella che, in condizioni stazionarie, assume la forma seguente:
[99]
ca la superficie di catalizzatore per unità di volume di particella. Il coefficiente di diffusione efficace Dieff contiene al suo
interno i contributi della porosità della particella catalitica,
della non linearità dello sviluppo dei suoi pori (la cosiddetta
tortuosità) e ovviamente del meccanismo di diffusione che vi
si instaura, sia esso di tipo molecolare o alla Knudsen. Se, per
semplicità, si considera un’espressione cinetica irreversibile
del prim’ordine (vi rs⫽⫺ksCi), e si assume che la particella sia
di forma sferica con raggio Rp, la [99] ammette la seguente
soluzione analitica:
Dieff ∇2Ci + Svνi rs = 0
che contempla sia il contributo della diffusione nei pori sia
quello della reazione chimica superficiale. Il termine Sv indi-
Cis
senh(φ X )
Xsenh(φ )
dove con X, Cis e / sono stati indicati, rispettivamente, la generica coordinata adimensionale (X⫽xⲐRp), la concentrazione del
reagente in corrispondenza della superficie esterna della particella e il modulo di Thiele. Quest’ultimo è un numero adimensionale che esprime l’importanza relativa dei fenomeni
diffusivi rispetto a quelli reattivi, definito come
[101] φ = Rp
Sv ks
Dieff
Tanto più / è piccolo e tanto più è facile il trasporto dei
reagenti all’interno della particella catalitica o equivalentemente la reazione chimica può essere considerata lenta rispetto ai processi diffusivi. Pertanto, come mostrato in fig. 8, il profilo di concentrazione in particella diviene sostanzialmente
piatto con concentrazione equivalente a quella esterna. Al contrario, all’aumentare del valore di /, il profilo di concentrazione mostra sensibili variazioni rispetto al valore della concentrazione esterna alla particella.
Per tener conto di questi fattori in termini integrali, riducendo quindi a un’unica relazione funzionale il comportamento
della particella catalitica per l’effetto combinato degli eventi
1,0
fig. 8. Andamento
della concentrazione
del reagente lungo il raggio
di una particella catalitica
sferica al variare del modulo
di Thiele /.
0,9
0,8
0,1
1
0,7
2
Ci(X)/Cis
0,6
/
0,5
5
0,4
10
0,3
0,2
20
0,1
0,0
0,0
0,2
0,4
0,6
0,8
1,0
x/Rp
276
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
chimici e del trasporto di materia intraparticellare, si definisce un termine, detto ‘efficienza del catalizzatore’ h, che esprime il rapporto tra la velocità di reazione media in particella e
quella che si avrebbe se nella particella fossero assenti fenomeni di tipo diffusivo e quindi tutta la reazione avesse luogo
alla concentrazione superficiale:
Vp
1
r (C ) dv
V p ∫0 s i
[102] η =
rs (Cis )
che, per il caso in esame, fornisce
[103] η =

1  3φ
−1
3φ 2  tanh(3φ ) 
il cui andamento è illustrato in fig. 9; efficienze di particella
pressoché unitarie si riscontrano solo per piccoli valori del
modulo di Thiele.
Per cinetiche complesse, come per esempio quelle trattate
in precedenza, o per particelle di forma diversa da quella sferica, è oltremodo improbabile riuscire a ottenere delle soluzioni analitiche e pertanto è necessario procedere a integrazioni numeriche. In termini pratici è però utile ricorrere a equazioni che esprimano in modo compatto l’efficienza della
particella catalitica in funzione di un gruppo adimensionale
tipo il modulo di Thiele. Le equazioni [101] e [103] sono state
così generalizzate per tener conto della non sfericità e della
non linearità della espressione cinetica:
[104] φ '' =
Vp
Sv rs (Cis )
Sp
Cis Dieff

1  φ ''
−1
[105] η = 2 
φ''  tanhφ '' 
dove Vp e Sp indicano, rispettivamente, il volume e la superficie esterna della particella, mentre la costante cinetica di pseudoprim’ordine può essere stimata dal rapporto tra la velocità
di reazione e la concentrazione del reagente principale in condizioni esterne (ks⬇rs(Cis)ⲐCis).
Reazioni gas-liquido
Nei sistemi gas-liquido, solitamente, solo alcuni dei prodotti di reazione e dei reagenti sono distribuiti tra le due fasi,
mentre nella stragrande maggioranza dei processi la reazione
chimica avviene in fase liquida. Pertanto, le espressioni cinetiche da impiegarsi sono analoghe a quelle derivate per i sistemi omogenei. Dato che però almeno la concentrazione di una
specie reagente è influenzata dal trasporto di materia attraverso l’interfaccia, oltre alla cinetica della reazione chimica, è
importante descrivere correttamente la quantità di materia scambiata attraverso l’interfaccia stessa. Ciò equivale alla conoscenza di due fattori: il flusso di materia tra le fasi e l’estensione dell’interfaccia. La reazione, se è particolarmente veloce, si localizza all’interno del film interfasico, ma generalmente
ciò avviene più nei processi di assorbimento (per esempio,
assorbimento di CO2 in soluzioni alcaline) che in veri e propri
processi volti allo svolgimento di una reazione chimica, quali
per esempio un’ossidazione, un’idrogenazione o una alogenazione. In definitiva, si può concludere che in questi sistemi gli
aspetti cinetici sono fortemente influenzati dagli aspetti inerenti il trasporto di materia. Facendo le debite proporzioni, la
trattazione delle reazioni gas-liquido può essere estesa anche
alle reazioni coinvolgenti due fasi liquide.
Un modo conveniente per stimare il flusso di materia interfasico ricorre alla teoria del doppio film, in base alla quale si
assume che le resistenze al trasferimento siano localizzate sia
nel film liquido sia in quello gassoso, assumendo inoltre che
le concentrazioni in corrispondenza dell’interfaccia rispettino
l’equilibrio termodinamico. Sotto tali condizioni, l’espressione del flusso di materia tra le fasi assume la forma
[106]
(
Ji = kcov,i CiG − Ki CiL
)
ov
kc,i
e Ki sono, rispettivamente, il coefficiente globale di
dove
trasferimento di materia e la costante di equilibrio di ripartizione; CiG e CiL indicano invece le concentrazioni nelle due fasi
del reagente interessato al trasferimento. Il coefficiente globale di scambio materiale, in accordo con la teoria del doppio
film, assume quindi la seguente espressione:
[107]
1
1
K
= G + iL
ov
kc,i kc,i E kc,i
G e k L sono i coefficienti di scambio materiale relativi
dove kc,i
c,i
alle due fasi in contatto ed E è il fattore di esaltazione che tiene
conto degli effetti delle reazioni veloci sul trasferimento di materia. Esso può essere stimato
a correlazioni basate sul
123
11ricorrendo
modulo di Hatta MH⫽冪DiLkrCBLⲐkL,i, dove DiL è il coefficiente
di diffusione in fase liquida della specie migrante, kr è la costante di velocità di reazione tra la specie gassosa e il reagente B in
fase liquida, e infine kL,i è il coefficiente di trasferimento di
materia in fase liquida. Nel caso limite in cui il reagente in fase
liquida sia in largo eccesso rispetto a quello trasferito dalla fase
gassosa, la reazione può essere considerata di pseudoprim’ordine e conseguentemente il fattore di esaltazione può essere stimato come E⫽MH ⲐtanhMH. L’equazione della velocità di reazione viene infine espressa ricorrendo alle concentrazioni della
fase nella quale la reazione stessa avviene (v. par. 5.1.8).
Reazioni non catalitiche gas-solido
10,000
h
1,000
1//
0,100
0,010
0,001
0,01
0,10
1,00
10,00
fig. 9. Andamento dell’efficienza h di una particella
catalitica sferica in funzione del modulo di Thiele /
per una reazione irreversibile del prim’ordine.
VOLUME V / STRUMENTI
/
100,00
Le reazioni non catalitiche dove uno o più reagenti in fase
gassosa sono posti in contatto con altri reagenti in fase solida
sono assai frequenti nella pratica industriale. Esempi significativi sono l’arrostimento di vari minerali, quali la pirite, la
blenda e la galena, la combustione del carbone, la rigenerazione di catalizzatori disattivati per formazione di depositi carboniosi e la riduzione di minerale ferroso. Anche in questi sistemi è sempre presente almeno un’interfaccia di separazione tra
le fasi, anche se solitamente le interfacce presenti sono almeno due: la prima tra la fase gassosa e il prodotto solido di reazione e la seconda tra il prodotto di reazione e il reagente solido originario. La reazione avviene sostanzialmente all’interfaccia tra il prodotto di reazione e il reagente solido. Pertanto
il reagente gassoso deve diffondere prima attraverso la fase
277
CINETICA E CATALISI
gassosa stessa in contatto con la particella solida (diffusione
esterna), poi attraverso il prodotto solido della reazione (diffusione interna) sino al raggiungimento dell’interfaccia di reazione, ove ha luogo la reazione vera e propria. Solitamente, dato
che la diffusione nei solidi è particolarmente lenta, la diffusione interna è lo stadio cineticamente limitante il processo, ma
esistono casi in cui lo stadio lento è costituito dalla reazione
superficiale. Comunque, dato che le dimensioni della particella e gli spessori dei vari strati evolvono nel tempo, esiste la possibilità che lo stadio lento del processo cambi nel tempo.
Un modello semplice che è spesso impiegato per descrivere la cinetica di queste reazioni è quello indicato come ‘modello a nucleo restringente’ (shrinking core), in cui il reagente solido è confinato in un nucleo centrale di dimensioni crescenti
nel tempo. Quindi, se si considera come riferimento una particella sferica di raggio Rp, inizialmente costituita dal reagente solido B, che reagisca con il reagente gassoso A per formare i prodotti solido N e gassoso M tramite la reazione
[108] A( g ) + ν B( s ) ⫺
⫺➤ M( g ) + N( s )
䉴
le velocità dei singoli stadi coinvolti, ossia diffusione esterna,
diffusione interna attraverso lo strato reagito e reazione superficiale (assunta per semplicità del prim’ordine rispetto al reagente gassoso e di ordine zero rispetto a quello solido), espresse in termini di portata molare così da comprendere la superficie dell’interfaccia di competenza, assumono le forme seguenti:
[109] FAG = 4 πRp2 kcG, A (C AG − C AS )
S
[110] FA =
4πRp xDAeff
Rp − x
(C AS − C iA)
[111] FAi = 4 πx 2 ksC Ai
dove x, k c,G A, DAeff e ks sono, rispettivamente, il raggio corrispondente all’interfaccia di reazione, il coefficiente di trasferimento di materia in fase gassosa del reagente gassoso, il suo
coefficiente di diffusione efficace nello strato solido reagito e
la costante cinetica della reazione superficiale; inoltre, CAG, CAS
e CAi sono, rispettivamente le concentrazioni del reagente gassoso nel cuore della fase gas, all’interfaccia tra il gas e il prodotto solido e all’interfaccia di reazione. Pertanto, la velocità
di trasformazione della particella per effetto dei tre contributi
precedenti assume la forma seguente:
−1

Re − x
1
1 
ov
G
+
+
[112] FA = 
 CA
eff
2 G
2
π
π
π
R
k
R
xD
x
k
4
4
4

p c, A
p
A
s
Infine, la velocità di consumo del reagente A [112] può
essere messa in relazione con quella del reagente solido B tramite la stechiometria della reazione:
3
2
d  4 πx  4 πx dx
=
= −ν FAov


dt  3VB 
VB dt
dove ṼB è il volume molare del reagente solido. Risulta quindi
evidente che la velocità di trasformazione di una particella solida dipende dalle sue dimensioni originarie, dalle proprietà di trasporto del reagente gassoso e dalla cinetica della reazione superficiale. L’equazione [113] può essere integrata così da ottenere
l’evoluzione, x, della conversione della particella nel tempo:
[113]
[114] ξ +
Rp kcG, A
1− 3(1− ξ )2/3 + 2(1− ξ )  +
2 DAeff 
+
278
3kc,GA
3kG CGνV
1− (1− ξ )1/3  = c, A A B t
ks
Rp
In conclusione, anche questo esempio mostra come nelle
reazioni eterogenee la cinetica della reazione sia, almeno in
linea di principio, influenzata dai fenomeni di trasporto.
5.1.10 Nuove tendenze nella stima
delle costanti cinetiche
Allo stato attuale delle cose, si può sicuramente affermare che
è possibile determinare la costante cinetica di ogni reazione
con un elevato livello di accuratezza usando i metodi della termodinamica statistica e della meccanica quantistica. In particolare, quest’ultima può essere impiegata per determinare la
superficie di energia potenziale nella reazione in esame e poi
il valore della costante può essere stimato o ricorrendo alla teoria dello stato di transizione sopra illustrata o a metodi di dinamica molecolare. Questa prospettiva è affiorata già nella prima
metà del 20° secolo con l’avvento della meccanica quantistica, ma importanti risultati quantitativi per qualsivoglia sistema reagente sono stati raggiunti solo con i progressi dei mezzi
di calcolo concretizzatisi verso il termine dello stesso secolo.
Oggi questi metodi consentono, per le reazioni in fase gassosa, accuratezze nella determinazione della costante cinetica
comparabili con quelle sperimentali, se non addirittura migliori. Ciò è particolarmente vero quando la reazione in esame faccia parte di un sistema complesso di reazioni dove sovente è
difficile isolare sperimentalmente il contributo di ciascun atto
reattivo.
Ovviamente, in questa sede non potranno essere esaminati i dettagli dei metodi che impiegano la meccanica quantistica. Nella sostanza, i metodi di stima delle costanti cinetiche
implicano la conoscenza dell’evoluzione dell’energia potenziale del sistema reagente nonché la valutazione delle frequenze
vibrazionali e rotazionali dei legami chimici coinvolti nella
reazione.
Il primo passo da compiere è quindi la determinazione della
superficie di energia potenziale: il cammino di minima energia individua ciò che comunemente viene chiamato coordinata di reazione. Questo calcolo viene effettuato mediante un criterio di approssimazione che sta alla base di tutti gli approcci
di chimica computazionale, ossia l’approssimazione di BornOppenheimer, per la quale, nel calcolo dell’energia di una molecola, risulta lecito separare i moti degli elettroni da quelli dei
nuclei, a causa della grande differenza esistente tra le loro masse.
È pertanto possibile calcolare l’energia dell’insieme degli elettroni della molecola per le diverse configurazioni ipotizzabili
dei nuclei. Nella sostanza, i programmi di calcolo oggi disponibili esaminano un insieme di configurazioni del sistema reagente intermedie tra quelle dei reagenti di partenza e quelle dei
prodotti finali, valutando per ciascuna di esse il valore dell’energia col fine ultimo di identificare lo stato di transizione. Ciò
premesso, si può osservare che l’energia totale di una molecola è costituita da una serie di termini quali l’energia cinetica di
ciascun elettrone, l’energia potenziale elettrostatica dovuta
all’interazione attrattiva tra elettroni e nuclei e repulsiva tra ciascuna coppia di elettroni e di nuclei e, infine, l’energia dovuta ai moti di traslazione, rotazione e vibrazione delle molecole. Questi ultimi due termini, in virtù dell’approssimazione citata, possono essere trattati separatamente dai primi due. I vari
metodi di calcolo si basano appunto su differenti approssimazioni introdotte nella valutazione dei termini predetti.
Un’importante categoria di metodi valuta gli orbitali molecolari come una combinazione lineare degli orbitali atomici
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
ricorrendo a funzioni d’onda monolettroniche e risolvendo il
sistema di equazioni non lineari che ne deriva tramite un approccio detto autoconsistente (metodi LCAO-SCF, Linear Combination of Atomic Orbitals-Self Consistent Field). L’errore
introdotto dall’uso di funzioni d’onda monoelettroniche viene
poi corretto tramite un approccio di tipo perturbativo (metodi
Moller-Plesset MP2, MP3, MP4, ecc., dove la cifra indica l’ordine dell’approssimazione introdotta). Questi metodi consentono stime accurate sia dell’energia di una molecola sia della
variazione di energia associata a una reazione chimica. Risultano però computazionalmente onerosi, per cui la loro applicazione è sostanzialmente limitata a sistemi in fase gassosa
comprendenti pochi atomi. Per ovviare a ciò, sono disponibili metodi semiempirici, quali quelli basati sulla teoria del funzionale di densità (DFT, Density Functional Theory), nel quale
il calcolo della distribuzione della densità elettronica permette stime accurate dell’energia con oneri computazionali inferiori a quelli dei metodi tipo MP. La semplificazione qui è nella
scelta di opportuni insiemi di funzioni di base che hanno insite le proprietà degli atomi in esame. Pertanto, il primo passo
da compiere nell’uso dei metodi DFT è quello di scegliere le
funzioni di base più opportune confrontando le stime dell’energia di formazione di alcune molecole campione con i corrispondenti dati sperimentali.
Negli ultimi trenta anni tutti questi metodi sono stati sviluppati in programmi di calcolo sofisticati, tra i quali possono essere citati: AMPAC e Gaussian. Essi sono inoltre
accompagnati da interfacce grafiche di ottimo livello che
consentono un’eccellente visualizzazione grafica dei risultati delle simulazioni. In definitiva è così possibile calcolare l’energia potenziale, e di conseguenza le geometrie di equilibrio, quelle dello stato di transizione, e le frequenze di vibrazione. Una volta note queste informazioni, l’applicazione di
metodi quali quello dello stato di transizione permette di ricavare il valore cercato della costante di velocità di reazione.
Ovviamente, i parametri così stimati possono avere valenza
qualitativa o quantitativa in funzione del livello della teoria
impiegata.
In linea di principio, le procedure di calcolo sopra citate
possono essere applicate sia alle reazioni in fase gassosa sia
a quelle su di una superficie solida. Mentre per le reazioni in
fase gassosa sono possibili stime molto buone, stime analoghe per reazioni superficiali costituiscono un compito più difficoltoso, in primo luogo perché è numericamente impossibile considerare esplicitamente il grande numero di atomi che
sono necessari per riprodurre la struttura e le proprietà di una
superficie. Per affrontare questo problema sono però disponibili due approcci. Il primo consiste nel considerare una cella
unitaria che comprenda un numero di atomi sufficiente a riprodurre la struttura elementare della superficie e successivamente imporre delle condizioni al contorno della stessa di tipo
periodico. Soluzioni di questo problema possono essere ottenute ricorrendo alla teoria del funzionale di densità per risolvere le equazioni della meccanica quantistica, e impiegando
onde piane quali funzioni d’onda base per gli elettroni. Il vantaggio di questo metodo consiste nel fatto che un grande numero di atomi può essere studiato con un formalismo sostanzialmente corretto. Il problema principale è invece dovuto alle
molte semplificazioni necessarie per ottenere un problema
trattabile numericamente, che abbassano sostanzialmente la
qualità dei risultati ottenuti. Un approccio alternativo consiste nel rappresentare la superficie tramite un insieme di atomi di dimensioni finite (cluster) e poi risolvere il problema
VOLUME V / STRUMENTI
considerando il cluster così individuato alla stregua di una
molecola isolata. Quest’approccio corrisponde a tagliare una
porzione della superficie dal reticolo completo. I legami liberi (dangling bonds) che si originano con questa procedura sono
poi solitamente saturati da atomi di idrogeno che hanno la funzione di rappresentare il legame originariamente presente con
il resto del cristallo di dimensioni infinite. Il vantaggio principale di quest’approccio è che l’accuratezza del metodo teorico quantomeccanico può essere bilanciata tramite le dimensioni del cluster, potendo così ricorrere a soluzioni raffinate
se si impiegano cluster di non elevate dimensioni. Il problema è però che sovente sono necessari cluster di grandi dimensioni per riprodurre correttamente le proprietà elettroniche
della superficie.
Sviluppo e analisi di schemi cinetici complessi
La disponibilità di programmi per la stima di costanti cinetiche molto affidabili e, tutto sommato, computazionalmente
non troppo onerosi per le attuali potenzialità di calcolo apre
nuove vie per la definizione e l’analisi di schemi cinetici complessi, costituiti nella loro interezza da reazioni elementari.
In termini generali, per definire nella sua interezza uno
schema cinetico, allorché complesso, si può far riferimento
all’approccio sistematico illustrato nel diagramma di flusso
riportato in fig. 10. Come primo passo, debbono essere individuate tutte le specie chimiche (sia neutre, sia radicaliche e ioniche) che probabilmente sono presenti nel sistema reagente, sia
in fase fluida sia adsorbite su un’eventuale superficie solida.
Questa individuazione deve essere guidata dalle conoscenze
chimiche esistenti sul sistema in esame e su sistemi analoghi
studiati in precedenza. Successivamente, debbono essere proposte tutte le possibili reazioni elementari coinvolgenti le specie precedentemente individuate. Infine, deve essere fornita
una stima della costante di velocità di reazione per ognuna di
esse. Per semplificare il tutto e ottenere schemi cinetici che
contengano solo le specie e le reazioni più significative è utile
poi ricorrere alla cosiddetta analisi di sensitività, ossia a una
tecnica in grado di fornire l’importanza relativa di ciascuna
reazione, così da identificare i cammini di reazione statisticamente più rilevanti. Occorre però precisare che le semplificazioni introdotte dall’analisi di sensitività limitano poi generalmente il campo di applicazione dello schema cinetico ridotto
a un ben preciso intervallo di temperatura, di pressione e di
composizione del sistema reagente.
5.1.11 Conclusioni e prospettive
Alla luce di quanto esposto, i presupposti teorici alla base dello
studio della cinetica delle reazioni chimiche sono oggi ben consolidati e permettono la definizione di schemi cinetici complessi come quelli che si incontrano, per esempio, nei processi di combustione degli idrocarburi, nella produzione di materiali avanzati per sintesi da reagenti gassosi e nei processi
catalitici eterogenei. Le teorie sono inoltre affiancate da metodi sperimentali sempre più efficaci che permettono l’individuazione quantitativa di specie chimiche che, pur se presenti
in piccola quantità, possono avere un ruolo estremamente importante nel condizionare la cinetica del processo, a causa della
loro alta reattività. Pertanto, diventano reperibili nella letteratura scientifica schemi cinetici basati su reazioni elementari in
grado di spiegare anche i comportamenti apparentemente anomali di un sistema reagente. Il grande sviluppo dei metodi di
279
CINETICA E CATALISI
identificazione di tutte le specie
chimiche eventualmente presenti
simulazioni del reattore
(cinetica ⫹ fluidodinamica)
identificazione sistematica di tutte
le reazioni possibili
analisi di sensitività
n⫽1
sì
n⫽n⫹1
analisi della reazione n
n⫽NTOT
n⫽n⫹1
no
sì
la costante cinetica della
reazione n è nota?
no
stima della costante cinetica
(TST, VTST, RRKM, ...)
scelta del metodo quantomeccanico
e del set di funzioni di base
identificazione (se esiste) e analisi
delle frequenze dello stato di transizione
ottimizzazione energetica della struttura
geometrica di reagenti e prodotti
analisi delle frequenze di reagenti
e prodotti
MP2, MP4, G2, ...
(ab initio)
B3LYP, B3PW91, ...
(DFT)
fig. 10. Diagramma di flusso delle operazioni che devono essere compiute per definire uno schema cinetico complesso.
calcolo permette poi di introdurre questi schemi cinetici in
modelli di reattori così da poter prevedere con grande dettaglio il loro comportamento.
In prospettiva sarà necessario estendere sempre più l’applicazione dei metodi della cinetica chimica non solo allo studio delle trasformazioni coinvolgenti organismi biologici, ma
anche alla previsione sia delle reazioni nell’alta atmosfera, per
le loro implicazioni di carattere ambientale, sia di quelle coinvolgenti particolari minerali nel profondo della crosta terrestre
per la verifica di teorie sulla genesi dei combustibili fossili o
sulla loro immobilizzazione in giacimenti profondi.
Carrà S., Zanderighi L. (1977) Reattività chimica: aspetti
cinetici, in: Enciclopedia della chimica, Milano, ISEDI, 6v.
Moore W.J. (1990) Chimica fisica, Padova, Piccin.
Moore J.W., Pearson R.G. (1981) Kinetics and mechanism,
New York, John Wiley.
Parr R.G., Young W. (1989) Density functional theory of
atoms and molecules, New York, Oxford University Press.
Steinfield J.I. et al. (1989) Chemical kinetics and dynamics,
Englewood Cliffs (NJ), Prentice Hall.
Elenco dei simboli
280
Bibliografia generale
Aj
Atkins P.W., Friedman R.S. (2004) Molecular quantum
mechanics, New York, Oxford University Press.
Benson S.W. (1976) Thermochemical kinetics: methods for the
estimation of thermochemical data and rate parameters,
New York , John Wiley.
Boudart M. (1968) Kinetics of chemical processes, Englewood
Cliffs (NJ), Prentice-Hall.
Carberry J.J., Varma A. (1976) Chemical and catalytic reaction
engineering, New York, McGraw-Hill.
Carrà S. (2004) Chimica computazionale, in: Enciclopedia
del Novecento, Roma, Istituto della Enciclopedia Italiana,
1975-2004, 13v.; v.XII: Supplemento III: Acqua-Guerra.
Carrà S., Morbidelli M. (1983) Chimica fisica applicata:
principi di termodinamica e cinetica chimica e loro ruolo
nella teoria del reattore chimico, Milano, Hoepli.
Ai
ai
bi
Ci
Dieff
DiL
dA, dB
E
Ej
Fi
F, Fcent
fi
fattore di frequenza della costante cinetica, unità
dipendenti dall’ordine di reazione
generica specie i-esima
attività della specie i-esima
costante di adsorbimento della specie i-esima
concentrazione della specie i-esima
coefficiente di diffusione efficace in mezzi porosi
coefficiente di diffusione in fase liquida
diametri molecolari delle specie A e B assimilate a
sfere rigide
fattore di esaltazione nello scambio materiale
interfasico
energia di attivazione della reazione j-esima
portata molare = flusso per superficie
fattori di Troe
fugacità della specie i-esima
ENCICLOPEDIA DEGLI IDROCARBURI
CINETICA DELLE REAZIONI CHIMICHE
gi
h
hi
Ki
Kj
kj
ks
ka
kc,i
kB
Ji
MH
mj
mA, mB
NA
NC
NR
oij
oj
P
P1/2
p
Q
R
Ri
Rp
rj
rij
rs
Si
Sp
Sv
T
Ṽi
Vp
VR
X
x
W(A, B)
Z(A, B)
parametro isoterma di adsorbimento ElövichTemking
costante di Planck
parametro isoterma di adsorbimento ElövichTemkin
costante termodinamica di equilibrio di fase (fattore
di ripartizione) per la specie i-esima
costante termodinamica di equilibrio della reazione
j-esima
costante di velocità della reazione j-esima, unità
dipendenti dall’ordine di reazione
costante di velocità della reazione superficiale,
unità dipendenti dall’ordine di reazione
costante cinetica pseudoprim’ordine per reazioni
monomolecolari
coefficiente di scambio materiale
costante di Boltzmann
flusso di materia interfasico
modulo di Hatta
esponente della temperatura nel fattore di frequenza
masse delle specie A e B collidenti
numero di Avogadro
numero di specie chimiche coinvolte nello schema
cinetico
numero di reazioni coinvolte nello schema cinetico
ordine di reazione della specie i-esima nella
reazione j-esima
ordine di reazione globale della reazione j-esima
pressione
pressione limite di falloff per le reazioni
monomolecolari
esponente di Troe
portata volumetrica di alimentazione al reattore
costante universale dei gas
produzione specifica della specie i-esima
raggio di particella
velocità della j-esima reazione
velocità di formazione della specie i-esima dalla
j-esima reazione
velocità della reazione superficiale
selettività rispetto al componente i-esimo
superficie esterna della particella di catalizzatore
superficie di catalizzatore per unità di volume di
particella
temperatura termodinamica
volume molare della specie i-esima
volume di particella
volume occupato dalla miscela reagente nel reattore
coordinata spaziale adimensionale
coordinata spaziale generica o posizione
dell’interfaccia
probabilità che una collisione bimolecolare dia
luogo alla reazione
numero di collisioni bimolecolari nell’unità di
tempo e di volume
VOLUME V / STRUMENTI
Lettere greche
a
esponente equazione cinetica di Tömking-Pyzev
variazione di energia libera associata alla reazione
DGj
j-esima
variazione di energia libera standard associata alla
DGj°
reazione j-esima
variazione di entalpia associata alla reazione
DHj
j-esima
variazione di entropia associata alla reazione
DSj
j-esima
DV*
variazione di volume molare tra stato attivato e
stato normale del reagente
e
energia della collisione
/
modulo di Thiele
coefficiente di attività della specie i-esima
gi
h
efficienza del catalizzatore
resa assoluta nel componente i-esimo
hi
resa relativa nel componente i-esimo
hir
m
massa ridotta delle due molecole collidenti
coefficiente stechiometrico della specie i-esima
vij
nella reazione j-esima
frazione di siti superficiali occupati dalla specie iÿi
esima
frazione di siti superficiali liberi
ÿv
s
sezione d’urto tra due molecole collidenti
tempo di residenza medio dei reagenti nel reattore
tR
conversione del reagente i-esimo
xi
Apici
eq
F
0
max
⬆
*
id
ad
L
G
S
ov
grandezza in condizioni di equilibrio
termodinamico
grandezza di una corrente di alimentazione
grandezza in condizioni iniziali
grandezza nel punto di massimo della funzione
grandezza relativa allo stato di transizione
reagente nel suo stato attivato
condizioni di soluzione ideale
condizioni di adsorbimento o specie adsorbite
grandezza in fase liquida
grandezza in fase gassosa
grandezza in corrispondenza di una superficie
grandezza globale
Pedici
i
j
specie chimica i-esima
reazione j-esima
Maurizio Masi
Dipartimento di Chimica, Materiali
e Ingegneria chimica ‘Giulio Natta’
Politecnico di Milano
Milano, Italia
281