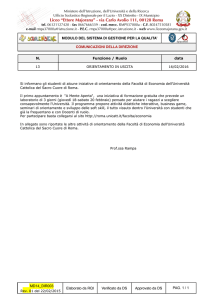
Dal criterio di stabilità meccanica alla Disuguaglianza diClausius
Consideriamo un caso di irreversibilità meccanica, Pe P, dove P = pressione interna e Pe =
pressione esterna.
Pe
A
irr
Pe
B
rev
rev
irr
B
V
espansione
A
V
compressione
L’irreversibilità consiste nell’esperienza comune secondo cui un sistema che possiede una pressione
interna tende ad aumentare di volume e mai a contrarsi, quando viene lasciato libero da vincoli
esterni. Viceversa, se lo si schiaccia esso diminuisce di volume. Detto in altri termini, se vogliamo
che l’espansione avvenga a velocità finita dobbiamo ridurre la pressione esterna di una quantità
apprezzabile rispetto a quella interna; allora il sistema si espanderà compiendo un lavoro positivo
sull’ambiente che, come si vede dal grafico, sarà inferiore a quello che farebbe nel caso reversibile,
in cui in ogni istante la pressione esterna è solo di un infinitesimo più bassa di quella interna.
Il caso reversibile comporta l’assenza di attriti, poiché il pistone non salirebbe con un P quasi
nullo, essendo bloccato dall’attrito. Nel caso reversibile potremmo riportare il sistema nello stato
originario esercitando, in ogni punto del percorso, una pressione di un infinitesimo superiore a
quella interna al sistema. Nel caso di un P finito abbiamo l’irreversibilità con o senza attrito: le
parti del sistema si deformeranno a velocità finita e parte dell’energia dovrà essere utilizzata per
metterle in movimento (energia cinetica). In presenza di attrito il P deve essere sufficiente a
vincere tali forze, altrimenti l’espansione non inizia neppure. Un piccolo attrito, sempre presente nei
fenomeni reali, è comunque “funzionale” allo smorzamento di tutti i moti e le oscillazioni e, quindi,
al raggiungimento di uno stato finale stabile, di equilibrio.
Il principio dell’orologio: “tutti gli orologi hanno bisogno della carica”, ovvero: non esiste l’orologio perfetto.
Un orologio perfetto è un meccanismo, complicato quanto vi pare che, dopo 24 ore, senza nessun apporto dall’esterno
ritorni esattamente nello stato del giorno precedente in ogni sua parte.
Per rendersi conto di cosa parliamo, basta prendere una siringa (senza ago) col pistone a metà corsa. Espandiamo il gas
tenendo chiusa l’apertura quindi rilasciamo il pistone. Questo tornerà verso la posizione iniziale a gran velocità,
vedremo al massimo una o due rapide oscillazioni, ma poi si fermerà. Se si potesse recuperare tutta l’energia del moto e
rimetterla come energia interna nel sistema, torneremmo esattamente allo stato iniziale. Ma non c’è verso di fermare il
moto se non facendo attrito in qualche modo. Quando questo avverrà, ci ritroveremo con un sistema e l’aria circostante
un po’ più caldi: infatti per sua natura l’attrito determina sempre il riscaldamento delle cose, mai il raffreddamento. Una
stessa quantità di aria, posta a temperatura maggiore, occuperà più volume. Se, con ostinazione, volessimo tornare allo
stesso volume iniziale e alla stessa temperatura, ci toccherebbe fare due cose: a) un po’ di lavoro aggiuntivo per
comprimere il gas; b) fare uscire un po’ di calore ponendo a contatto la siringa con aria a temperatura più bassa.
Quindi, alla fine del ciclo, il risultato netto sarebbe che avremmo fatto un po’ di lavoro per riscaldare un po’ d’aria
esterna. Uno dei modi di enunciare il secondo principio della termodinamica afferma che “è impossibile effettuare una
trasformazione ciclica di un sistema senza che nell’ambiente, che si trova in equilibrio termico e meccanico con esso,
un po’ di energia meccanica si trasformi in calore”. In base a ciò che abbiamo imparato sul rapporto Q/T, tale quantità
di calore, divisa per la temperatura dell’ambiente, corrisponde all’aumento di entropia complessivo del sistema e
dell’ambiente (per il sistema l’entropia non può cambiare, poiché ritorna esattamente nello stesso stato iniziale). In
forma più generale, dal secondo principio discende anche che: “in un sistema isolato non possono mai avvenire
trasformazioni in cui tutti i sottosistemi ritornano nelle condizioni iniziali”. Questo enunciato potrà anche sembrare
molto solenne e profondo, ma non aggiunge assolutamente nulla alla nostra esperienza comune che per fermare le cose
ci vuole attrito, il quale produce un calore da cui non si recupera mai una quantità equivalente di energia meccanica.
Se, una volta effettuata l’espansione, vogliamo ritornare allo stato iniziale, non potremmo mai farlo
attraversando a ritroso gli stati il percorso di espansione irreversibile: infatti in tale percorso la
pressione esterna tornerebbe ad essere inferiore alla pressione interna del sistema e, in tal caso,
questo non potrebbe mai comprimersi; per la semplice ragione che non si è mai visto qualcosa
comprimersi da solo se lasciato libero di espandersi. Tornare al percorso iniziale è comunque
possibile (seconda figura), ma solo con un percorso dove le pressioni sono maggiori di quella del
sistema, stato per stato, punto per punto. Questo comporterà l’effettuazione di una quantità di lavoro
sul sistema, cioè un lavoro negativo, maggiore in valore assoluto di quello “ricavato” nel percorso
di espansione. Il percorso di compressione reversibile sarà quello che ci consentirà di “consumare”
meno energia, essendo in ogni istante la pressione solo di pochissimo maggiore di quella del
sistema. Vediamo un esempio numerico, con valori arbitrari.
Irrev. EAB = Qirr - Lirr
Espans.
Compress.
es. 75 – (+15)
-85 - (-25)
EAB = Qrev – PdV rev es. 80 – (+20)
-80 - (-20)
B
EAB = Qirr – Pe dV
Pe Pint
irr
A
Rev.
EAB = Qrev – Lrev
B
Pe = Pi
A
Sia nel caso di un’espansione, che nella compressione, le trasformazioni reversibile e irreversibile
tra gli stessi stati iniziale e finale A e B, comportano Lrev > Lirr e conseguentemente Qrev > Qirr, se
EAB deve rimanere lo stesso. Una conseguenza di questa conclusione è che
dQ rev B dQirr
A T > A T
Poiché il primo integrale a sinistra è indipendente dal percorso, il suo valore può essere espresso
come la variazione di una funzione primitiva S tra i due stati A e B. La funzione S è chiamata
entropia. La precedente disuguaglianza (di Clausius) diventa:
B
B
dQ irr
T
A
Ogni piccola quantità dQirr di calore acquistata dal sistema corrisponde a un calore –dQirr in uscita
dall’ambiente e viceversa. In aggiunta, per l’ambiente, inteso come serbatoio di calore, o batteria di
serbatoi di calore, non esistono percorsi diversi per trasformazioni reversibili e irreversibili, per
questo per esso. In altre parole, gli stati dell’ambiente, un semplice serbatoio di calore, sono identici
a parità di energia interna (invece un sistema con variabili meccaniche può avere, a parità di
contenuto energetico, maggiore temperatura e minore pressione rispetto a un altro stato). Quindi si
può scrivere:
Ba
Ba
B
dQ
dQ
dQ irr
Sa = a _ rev = a _ irr = –
T
T
T
A
Aa
Aa
S >
I pedici in Aa e Ba stanno a indicare gli stati dell’ambiente che, ovviamente, non hanno nulla a che vedere con gli stati
del sistema. Chiaramente gli stati A e Aa sono tali da essere in equilibrio termico, meccanico chimico ecc. tra loro e lo
stesso si può dire di B e Ba. Calcolando la variazione di entropia totale si ha:
dQ rev B dQ irr
ST = S + Sa =
–
> 0 (in base alla disuguaglianza di Clausius)
T
T
A
A
L’insieme sistema + ambiente può essere chiamato sistema isolato, o universo (in senso relativo).
Per esso vale quindi:
ST > 0 (per un processo irreversibile).
B
La variazione di entropia complessiva è nulla solo per un ipotetico processo reversibile: ST rev = 0.