LA FORZA DI COULOMB
LA LEZIONE
LA LEGGE 1/R2
Richard Feynman, nel secondo volume delle sue lezioni, nel paragrafo dedicato alla
legge di Coulomb, scrive: “Sembra che Benjamin Franklin sia stato il primo ad
accorgersi che il campo dentro un involucro conduttore è nullo. Il risultato gli sembrò
strano. Quando riferì la sua osservazione a Priestley, questi suggerì che la cosa
potesse essere messa in relazione con una legge di quadrato inverso, perché si
sapeva che un guscio sferico di materia non produce alcun campo gravitazionale
nell’interno. Tuttavia Coulomb non misurò la dipendenza dal quadrato inverso se non
18 anni dopo e la legge di Gauss venne ancora più tardi.”
fig.1 - Macchina elettrostatica di Priestley; fig.2 - Schema per la dimostrazione che
all’interno di un conduttore gli effetti elettrici sono nulli
La misura della forza elettrica da parte di Charles Augustin de Coulomb avvenne nel
1785. Il riferimento alla legge dell’inverso del quadrato di Joseph Priestley si trova nel
volume “The history and present state of electricity with original experiments”
pubblicato nel 1767. Poche righe a conclusione di un’esperienza in cui si osservava
che gli oggetti all’interno di un conduttore carico non sembravano mostrare effetti
elettrici.
“Possiamo noi non inferire da questo esperimento che l’elettricità è soggetta alla
stessa legge della gravitazione, e quindi in accordo ai quadrati delle distanze; poiché
si può facilmente dimostrare che nel caso in cui si consideri la terra come un guscio
sferico, un corpo al suo interno non sarà attirato da una parte più che dall’altra.”
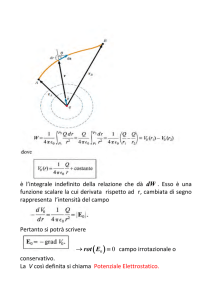
Se si disegna un guscio di spessore trascurabile con una densità di massa uniforme ρ,
la forza agente su un corpo posto in un punto P generico al suo interno dovuta alla
massa ρdS1 sull’areola 1 è esattamente bilanciata dalla forza dovuta alla massa ρdS 2
della superficie 2 solo quando F è proporzionale a 1/r2. In questo modo nella seconda
metà del Settecento si delineò la possibilità di dimostrare che anche la forza tra
cariche seguisse la stessa dipendenza dalla distanza della forza di attrazione
gravitazionale, semplicemente misurando la carica all’interno di un conduttore con un
elettrometro. Il personaggio che realizzò un simile compito nel 1773 fu Henry
Cavendish, ma alcune delle sue ricerche settecentesche furono pubblicate solo un
secolo dopo grazie a James Clerk Maxwell.
fig.3 - Tavola dal lavoro di Cavendish del 1771 sui fenomeni elettrici spiegati nei
termini di un fluido elastico
Nel 1771, in un’opera prettamente matematica, Henry Cavendish esponeva la teoria di
un fluido che doveva spiegare i fenomeni elettrici grazie a leggi di forza dipendenti
dalla distanza. Confrontando le stilizzate tavole allegate al lavoro e la classica
iconografia della scienza elettrica dimostrativa dell’epoca si ha la sensazione di uno
scienziato lontano dalla sensibilità e dagli interessi dei cultori dei fenomeni elettrici.
Dopo molti tentativi di misurare la forza elettrica (Stephen Gray, Daniel Bernoulli,
John Robinson), solo con Coulomb nel 1785 si avviò una prima valutazione della legge
1/r2 grazie alla sua bilancia di torsione nel caso delle forze tra cariche dello stesso
segno. La forza tra cariche opposte era misurata dal francese con un apparato
diverso, più vicino a quello impiegato da altri scienziati. Tutte le misure, non
particolarmente precise, erano corrette valutando la perdita di carica delle sferette
nell’aria. La nuova legge apriva la strada all’elettrostatica quantitativa e affiancava,
come abbiamo già ricordato, le ricerche di Volta sui concetti di capacità, carica e
tensione.
fig.4 - Bilancia di Coulomb del 1785 ; fig.5 - Apparato sperimentale di Coulomb per
lo studio della repulsione tra cariche; fig.6 -Tavola di Coulomb che riporta i valori
delle misure delle variazioni della carica di un conduttore a contatto con l’aria
MAXWELL E CAVENDISH
Cavendish, nel tentativo di determinare la legge della forza elettrica in funzione della
distanza tra le cariche, si affidò a un apparato descritto minuziosamente nei suoi
appunti e disegnato con uno schizzo. Nel seguito sono riportati il frontespizio della
pubblicazione postuma delle ricerche sull’elettricità di Cavendish (1879), lo schema
del dispositivo realizzato dall’autore, il disegno dell’apparato presente sempre nel libro
del 1879 curato da Maxwell.
fig.7 - Il frontespizio della stampa del
1879 delle ricerche elettriche di
Cavendish curata da Maxwell
fig.8 - Schizzo dell’apparato di Cavendish tratto dagli appunti dell’autore;
fig.9 - Riproduzione dell’apparato di Cavendish per la misura della carica interna di un
conduttore
Due calotte conduttrici erano montate su un telaio di legno incernierato in modo da
riunire le calotte in un’unica sfera cava. Al suo interno poteva essere disposta e fissata
una seconda sfera metallica di raggio inferiore alla prima, comunicante con l’esterno
grazie a due manici isolanti che attraversavano il globo cavo. La sfera, di raggio
minore, inizialmente era collegata elettricamente alla superficie interna della sfera più
grande tramite un corto conduttore che poteva essere rimosso tirando un filo che
fuoriusciva all’esterno. L’intenzione dell’esperimento era capire se elettrificando la
superficie esterna, quella interna si fosse caricata. La misura dell’eventuale carica
residua nel globo più piccolo, una volta rimossa la sfera esterna e il collegamento
elettrico tra le due superfici, era osservabile in linea di principio grazie alla
divaricazione di una coppia di pendolini elettrici. Il rudimentale elettrometro avrebbe
permesso di valutare la legge della forza elettrica.
Andiamo con ordine, seguendo la descrizione del procedimento data da Maxwell nel
Treatise del 1873. Dopo aver caricato con una bottiglia di Leida le emisfere riunite,
Cavendish immediatamente apriva il globo esterno, togliendo, al tempo stesso, con il
filo, il collegamento elettrico interno. Allontanava l’involucro esterno e avvicinava
“l’elettrometro” alla superficie della sfera più piccola senza ottenere alcuna
divaricazione. Ciò non poteva però escludere la presenza di un’eventuale carica, non
rilevabile dall’apparato di misura. Per valutare la sensibilità della sua apparecchiatura
Cavendish, lavorando adesso sul globo più piccolo, forniva a esso frazioni del valore
originario della carica iniziale della bottiglia di Leida.
“Trovò così -scriveva Maxwell- che la carica acquistata dalla sfera era inferiore a 1/60
della carica dell’intero apparato poiché se fosse stata superiore, sarebbe stata rilevata
dall’elettrometro.” Solo con carica nulla la legge di potenza della forza sarebbe pari a
1/r2. La presenza di una carica residua avrebbe modificato di una piccola quantità q
l’esponente, con la forza proporzionale a -2+q.
“Egli allora calcolò -continuava Maxwell- il rapporto della carica del globo con quello
delle emisfere nell’ipotesi che la repulsione fosse inversamente proporzionale a una
potenza della distanza che differiva leggermente da 2 e trovò che questa differenza
fosse 1/50, essa avrebbe portato a una carica del globo pari a 1/57 di quella
dell’intero apparato, e quindi misurabile dall’elettrometro.” p. 81, J. C. Maxwell, “On
the Proof of the Law of the Inverse Square” da A Treatise on Electricity and
Magnetism, 1873
L’uso delle frazioni è indice della difficoltà di calcolo. Peraltro Maxwell nella sua
trattazione utilizzava il potenziale elettrico delle sfere, mentre Cavendish non
padroneggiava, se non in forma embrionale, i fondamenti dell’elettrostatica.
Il fattore correttivo della legge di Coulomb secondo l’esperimento settecentesco
doveva essere pari a 1/50. In termini odierni l’esponente della legge di forza
assumeva il valore 2 con un’incertezza relativa dell’ordine dell’1%.
L’esperimento fu ripetuto da Cavendish sostituendo i conduttori di forma sferica anche
con dei parallelepipedi, ottenendo risultati confrontabili. Maxwell invece, cento anni
dopo, replicò l’esperimento di zero con alcune migliorie impiegando un elettrometro a
quadranti di Thomson, capace di rilevare cariche piccolissime rispetto a quella del suo
illustre predecessore. Le misure, esplicitate adesso in forma di potenziale dipendente
dai due raggi delle sfere, furono pubblicate nel 1873.
Nel Cavendish Laboratory la verifica della legge di Coulomb portò Maxwell a una
potenza per la funzione 1/rn che poteva essere compresa tra 2-1/21600 e 2+1/21600.
Bisognava attendere oltre sessanta anni per migliorare questa valutazione.
GLI ESPERIMENTI DEL NOVECENTO
Nel 1936 i fisici americani S. J. Plimpton e W. E. Lawton del Worcester Institute
diedero un nuovo impulso alla verifica sperimentale della legge di Coulomb alla
Cavendish-Maxwell. Invece di impiegare due sfere, il conduttore interno era a forma di
calotta. La differenza di potenziale tra i due conduttori era misurata in modo continuo
attraverso un voltmetro posto all’interno dell’apparato, osservabile con un telescopio e
uno specchio attraverso un piccolo foro praticato nella sfera. La chiusura dell’apertura,
con vetro e una soluzione salina, limitava la disomogeneità del potenziale del
conduttore esterno. Il potenziale era controllato da una tensione alternata. Dopo aver
calibrato il sistema di misura, si osservavano valori del voltmetro interno dell’ordine
del milionesimo di volt. La correzione q alla legge di potenza della forza doveva essere
minore di 2 10-9.
fig.10 - Schema dell’apparato sperimentale di
Plimton e Lawton del 1936
La frequenza della tensione sinusoidale utilizzata nell’esperimento era di soli 2 Hz,
corrispondente alla frequenza di risonanza caratteristica del voltmetro. In tal modo si
cercava di rendere trascurabili gli effetti del rumore nelle misure di potenziale. Dopo
oltre trenta anni lo sviluppo dell’elettronica permise un nuovo salto nella valutazione
della precisione della legge di Coulomb, con l’utilizzo di amplificatori ad aggancio di
fase.
Gary D. Cochran con una tesi del 1967 fu il primo a lavorare in questa direzione. Negli
anni successivi, tra il 1968 e il 1971, tre diversi gruppi migliorarono la precisione del
calcolo di q. Limitandoci all’esperimento di Princeton di D. F. Bartlett, P. E. Goldhager,
E. A. Philipps, lo schema di Cavendish era rielaborato con l’utilizzo di cinque sfere
concentriche (il gruppo di E. R. Williams, J. E. Faller, H. A. Hill impiegò invece degli
icosaedri). Le due sfere più esterne costituivano un primo condensatore separato da
un secondo capacitore costituto dalle due più interne. Il conduttore centrale costituiva
lo schermo tra i condensatori. Alle sfere più esterne era applicata una differenza di
potenziale alternata e si esaminava la tensione interna, in fase con il primo,
caratteristica del secondo condensatore; dopo aver inviato all’amplificatore, posto in
parallelo al condensatore più interno, un segnale con la stessa frequenza della
tensione alternata.
fig.11 - Test della legge di Coulomb effettuato nel 1970 nell’Università di Princeton ;
fig.12 - Apparato sperimentale del 1971 di Williams, Faller, Hill per la verifica della
legge di Coulomb
A tale scopo una lampada al neon, alimentata dalla stessa differenza di potenziale
alternata, costituiva il segnale luminoso che era convertito da un fotodiodo, posto
all’ingresso dell’amplificatore, in corrente elettrica. Oltre a valutare il fattore correttivo
inferiore o uguale a 1,3 10-13, Bartlett e collaboratori, nel lavoro Experimental test of
Coulomb’s law del 1970, chiarivano un modo diverso di parametrizzare le piccole
variazioni della legge di potenza tra cariche. I tre autori scrivevano:
“In alternativa, seguendo de Broglie, possiamo pensare di generalizzare le equazioni
di Maxwell nel modo più semplice e affascinante. Se il fotone avesse una massa a
riposo m piccola diversa da zero, le due cariche si respingerebbero secondo una forza
alla Yukawa, derivata dal potenziale U(r)=e-krr-1, dove k=2mc/h è l’inverso della
lunghezza Compton del fotone.”
In altre parole invece di avere come nel caso elettrostatico un potenziale dipendente
solo dall’inverso della distanza tra cariche l’ipotesi di una finitezza della massa del
fotone implicherebbe k diverso da zero e la forza tra cariche si modificherebbe nella
forma:
F=Q1Q2(1/r2+k/r e-kr)/4πε0
La forza tra cariche puntiformi non seguirebbe, accettando l’ipotesi di Louis de Broglie
del 1940 di un fotone con massa diversa da zero, le legge dell’inverso del quadrato
della distanza, ma presenterebbe un termine correttivo dipendente dalla piccola
massa. Sviluppando in serie di potenze U(r) i fisici americani riscrivevano il potenziale
nella forma 1/r – k +k2r/2, concludendo che la differenza di potenziale era allora
dipendente dal quadrato di k. Di sfuggita indicavano per le loro misure un valore di k
inferiore o uguale a 10-8 cm-1.
Solo nel gennaio 1971, Williams, Faller e Hill, con l’articolo “New experimental test of
Coulomb’s law: a laboratory upper limit on the photon rest mass”, presentavano per
la prima volta una tabella di corrispondenza tra il fattore di correzione q alla legge di
potenza e la massa a riposo del fotone, sia nel caso delle misure relative alla legge di
Coulomb, sia riprendendo le valutazioni di altri autori che analizzavano le modifiche
delle leggi dell’elettromagnetismo di Maxwell conseguenti all’introduzione della massa
intrinseca del fotone.
fig.13 - Tavola riassuntiva dei valori del test della legge di Coulomb e del valore limite
della massa di riposo del fotone fino al 1970
fig.14 - Le ricerche recenti sulla massa a riposo del fotone
In questo lavoro era ancora più evidente il richiamo alla generalizzazione delle
equazioni di Maxwell, in una forma associata al nome di Alexandre Proca.
Discuteremo in una prossima lezione in dettaglio la questione della massa del fotone.
Qui basti ricordare che oggi gli scienziati cultori dell’argomento sono ridotti a una
sparuta minoranza e tracce delle loro ricerche possono essere ritrovate nella rassegna
sulla fisica delle particelle sul sito alla voce gamma (γ) mass.