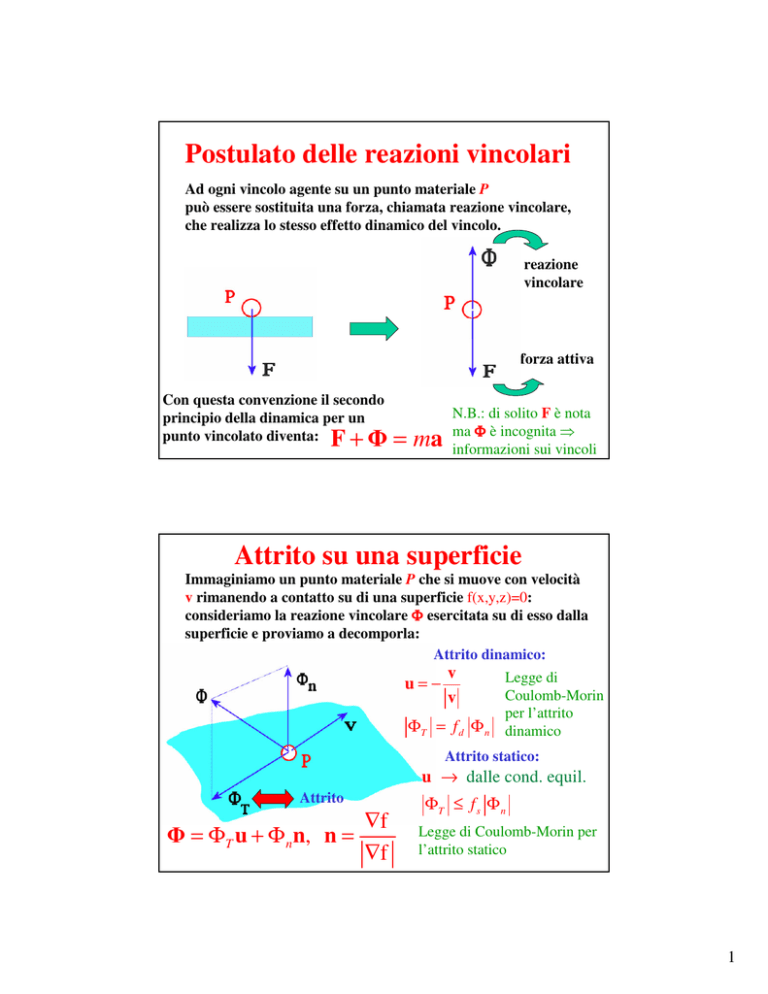
Postulato delle reazioni vincolari
Ad ogni vincolo agente su un punto materiale P
può essere sostituita una forza, chiamata reazione vincolare,
che realizza lo stesso effetto dinamico del vincolo.
reazione
vincolare
forza attiva
Con questa convenzione il secondo
principio della dinamica per un
punto vincolato diventa:
F+
= ma
N.B.: di solito F è nota
ma Φ è incognita
informazioni sui vincoli
Attrito su una superficie
Immaginiamo un punto materiale P che si muove con velocità
v rimanendo a contatto su di una superficie f(x,y,z)=0:
consideriamo la reazione vincolare Φ esercitata su di esso dalla
superficie e proviamo a decomporla:
Attrito dinamico:
v
Legge di
u=−
Coulomb-Morin
v
per l’attrito
ΦT = f d Φ n dinamico
Attrito statico:
Attrito
= ΦT u + Φ nn, n =
u → dalle cond. equil.
∇f
∇f
ΦT ≤ f s Φ n
Legge di Coulomb-Morin per
l’attrito statico
1
Cono di attrito
ϕd =
ϕs =
tgα =
angolo di attrito dinamico:
ΦT
tgϕ d =
= fd
Φn
angolo di attrito statico:
tgϕ s = f s
ΦT
≤ f s = tgϕ s
Φn
α ≤ ϕs
Equilibrio di una particella
(o punto materiale)
Una posizione è di equilibrio per un punto materiale P se,
posto il punto in essa con velocità nulla al tempo iniziale t = 0,
vi rimane indefinitamente per ogni t ≥ 0,
ovvero, se il punto resta sempre fermo, cioè in quiete.
Condizione necessaria e sufficiente per l’equilibrio
di un punto materiale soggetto ad un sistema Σ di forze
è che valga l’equazione:
coordinate di P : 3 incognite
Ftotale = 0
F ( P , 0, t ) +
N.B: 3 equazioni scalari in
6 incognite
forza attiva:
probl. staticamente indeterminato.
nota
Per risolverlo occorre rendere
num. eqz. = num. incognite
probl. staticamente determinato
=0
reazione vincolare:
incognita (3
incognite scalari)
2
Equilibrio di un corpo
(cioè, di un sistema di punti materiali)
Una configurazione è di equilibrio per un corpo se,
posto il corpo in essa con atto di moto nullo al tempo iniziale t = 0,
vi rimane indefinitamente per ogni t ≥ 0,
ovvero, se il corpo resta sempre fermo, cioè in quiete,
ovvero se tutte le particelle del corpo restano sempre in quiete.
Condizione necessaria e sufficiente per l’equilibrio di un sistema
di punti materiali (s = 1, 2, …, n), soggetto ad un sistema Σ di
forze, è che valgano le seguenti equazioni:
∀Ps ∈ insieme dei punti liberi
Fs = 0,
Fs +
s
= 0 ∀Ps ∈ insieme dei punti vincolati
Ci sono due metodologie per determinare le posizioni
di equilibrio di un corpo (sistema di punti materiali):
• le equazioni cardinali della statica
• il principio dei lavori virtuali
Le equazioni cardinali della statica
Condizione necessaria per l’equilibrio di un corpo qualsiasi,
soggetto ad un sistema Σ di forze, è che valgano le equazioni:
R (e) = 0
R (e,a) + R (e,v) = 0
M (e) = 0
M (e,a) + M (e,v) = 0
N .B. : Ω polo qualsiasi; tutte le forze sono del tipo F( P, 0, t )
3
Equilibrio di un corpo rigido
Condizione necessaria e sufficiente per l’equilibrio di
un corpo rigido, soggetto ad un sistema Σ di forze,
è che valgano le equazioni:
R (e) = 0
R (e,a) + R (e,v) = 0
il c.r non trasla
M (e) = 0
M (e,a) + M (e,v) = 0
il c.r. non ruota
N . B.1: Ω polo qualsiasi; tutte le forze sono del tipo F( P, 0, t )
N.B.2: le operazioni elementari (ed i conseguenti teoremi di riducibilità)
lasciano invariati sia il risultante che il momento risultante del
sistema di forze Σ applicato ad un corpo,
nel caso dei c.r. queste operazioni non possono alterare l’equilibrio.
N.B.3: le eqz. cardinali sono C.N. e S. per trovare l’equilibrio, non per la
determinazione delle reazioni vincolari.
Equilibrio di sistemi
costituiti da corpi rigidi
Condizione necessaria e sufficiente per l’equilibrio di un sistema
scomponibile in sottosistemi rigidi è che ogni sua parte rigida sia
in equilibrio.
Esempio:
Il sistema è posto in un
piano verticale, sul quale
agiscono le forze peso.
Le 2 aste sono collegate
fra loro in A mediante
una cerniera (sferica),
assimilabile ad un punto
materiale.
Quindi, dobbiamo scrivere le eqz. cardinali per entrambe le aste OA e
AB, tenendo presente che nella cerniera A vale il principo di azione e
reazione:
4
N.B.:
È arbitrario a chi
attribuire il segno +
Cosa significa questo per il nodo A? Usiamo il free body diagram:
Allora, oltre alle 2 aste, anche la cerniera in A, pensata come un
punto materiale, deve essere in equilibrio: − A + A = 0
5
Allora, possiamo supporre che la stessa condizione valga anche nel caso
in cui ci siano delle forze attive che agiscono sulla cerniera in A:
in generale, occorre allora richiedere per l’equilibrio un sistema
articolato (aste collegate fra loro mediante cerniere),
oltrechè le condizioni di equilibrio di ogni parte rigida, anche
la condizione di equilibrio per ciascun nodo (inteso come punto
materiale).
Mostriamo ora come diventa il
calcolo nell’esempio
precedente, supponendo che
sulla cerniera in A agisca anche
una forza attiva F.
In questo caso chiameremo:
≡ azione esercitata dalla cerniera sull'
estremo A dell'
asta OA
− 1 ≡ azione esercitata dall'
asta OA sulla cerniera in A
estremo A dell'
asta AB
2 ≡ azione esercitata dalla cerniera sull'
− 2 ≡ azione esercitata dall'
asta AB sulla cerniera in A
1
6












