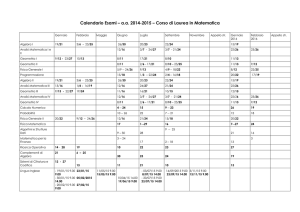
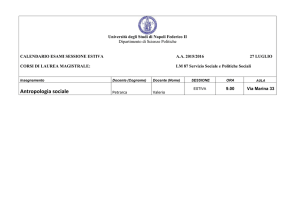
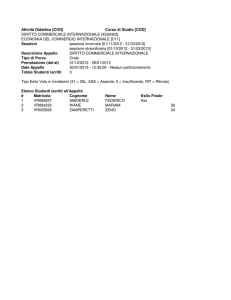
MATEMATICA GENERALE Prof. Valerio Lacagnina II appello

MATEMATICA GENERALE
II appello, SESSIONE AUTUNNALE 2014/15
Prof. Valerio Lacagnina
TEMA 1
•
Studiare la funzione
•
Determinare, al variare del parametro ∈ ℝ, quando il sistema ammette autosoluzioni:
•
Data la funzione
= − − + 2 + 3 − 2 + 2 = 0
− + = 0 − 1 − = 0
= + ln
determinare il polinomio di Taylor di punto iniziale = 1 arrestato al 3° ordine.
•
Determinare il carattere della serie
2
1
E' obbligatorio svolgere lo studio di funzione.
MATEMATICA GENERALE
II appello, SESSIONE AUTUNNALE 2014/15
Prof. Valerio Lacagnina
Soluzioni Tema 1
1 = √ − ; C. E. : − ≥ 0 ⇒ − ≤ 0 ⇒ − 1 ≤ 0 ⇒ ≤ 1,funzione che non ha
simmetrie rispetto l'origine con 0 = 1 = 0
lim − = +∞; lim
-→/
2 =
lim9
-→
limD
-→
2 − 3
-→/
2 √ − 2 − 3
2 √ − 2 − 3 2 √ − ≥ 0con5 2 = 5\{0,1}
= lim9
-→
= limD
-→
2 − 3
2 1 − 2 − 3
2 1 − ossia = 0 è punto angoloso.
lim
E
:;
;=
2;<;
− 3
-→9 2 @A
−AC
√ABA
→D
√ − − = − lim 1
= − lim √1 − = +∞
-→/
-→/
= lim9
-→
= limD
-→
2 − 3
2− √1 − 2 − 3
2 √1 − = lim9
-→
= limD
-→
2
−2
>
>
:
<;
=
2;−
3
1 − ?@ABAC
:
<;
=
2;−
3
1 − ?@ABAC
>
>
= −1
=1
= −∞Flessoatangenteverticaledx
2
2 ≥ 0per2 − 3 ≥ 0 ⇒ 3 − 2 ≤ 0 ⇒ 3 − 2 ≥ 0 ⇒ 0 < ≤ conmassimoin
3
2
2 2 4 8
12 − 8
2
R S = 1R S − R S = 1 −
= 1
=
= 0.38
3
3
3
9 27
27
3√3
22 − 3 − 22 − 6 − − 2 − 3 2√
22 =
=
=
4 − 4√ − − 26 Y − 8 + 2 − 4 + 12 − 9 Y 12 Y − 16 + 4 − 4 + 12 − 9 Y
=
=
=
4√ − − 4√ − − 3 Y − 4 3 − 4
= ≥0
=
4√ − − 4√ − − Passiamo allo studio della derivata seconda:
2 − 62√ − − 2 − 3 Poiché il denominatore è sempre positivo nel campo di esistenza della derivata seconda, si studia solo il
numeratore
≥ 0 ⇒ > 0 dato il dominio di 22 ;
4
3 − 4 ≥ 0 ⇒ ≥ > 1
3
da cui la funzione rivolge la concavità verso l'alto per < 0 e la concavità verso il basso per 0 < < 1.
2
E' obbligatorio svolgere lo studio di funzione.
MATEMATICA GENERALE
II appello, SESSIONE AUTUNNALE 2014/15
Prof. Valerio Lacagnina
− + 2 + 3 − 2 + 2 = 0
2 − + = 0 ilsistemaammetteautosoluzionesenonèapienorango ⇒
− 1 − = 0
− + 2 3 − 2 2
^
1
−1
1^ = − 1)3 − 2) − 2 + 2 − 1) + − + 2) =
− 1)
−
0
= 3 − 5 + 2 − 2 + 2 − 2 + − + 2 = 2 − 2 = 0 ⇒ − 1) = 0 ossia il sistema
ammette autosoluzioni per = 0 ∨ = 1.
3 = + lnscriverelaformuladiTaylordipuntoiniziale = 1arrestataal3°ordine
) = + ln ; 1) = 1
1
2 ) = 1 + ; 2 1) = 2
1
22 ) = − ; 22 1) = −1
2
′22 ) = ; 222 1) = 2
e quindi la formula di Taylor richiesta è
) ≃ 1 + 2 − 1) −
− 1) − 1)
+
2
3
3
E' obbligatorio svolgere lo studio di funzione.
MATEMATICA GENERALE
II appello, SESSIONE AUTUNNALE 2014/15
2
2 2
4 = 2 = 2 R S applicoilcriteriodellaradice
2 2
1
lim
R S = ijk = 0 laserieconverge.
g→
→ h
4
E' obbligatorio svolgere lo studio di funzione.
Prof. Valerio Lacagnina