Equilibrio redox File

BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Equilibrio di ossido-riduzione
1.
Unità elettriche
La quantità di elettricità (Q) viene misurata in coulomb, che è l'unità pratica di carica
elettrica. Un elettrone ha carica – 1,6.10-19 C .
L’ intensità della corrente elettrica (I) rappresenta la velocità di trasferimento della
carica: la sua unità pratica è l'ampère (A), pari ad un coulomb di elettricità trasferita
in un secondo. A = C/s
La differenza di potenziale (V) tra due punti di un conduttore causa il trasferimento
di una carica da un punto all'altro del conduttore. Il volt è l'unità pratica di
differenza potenziale ed è pari al rapporto tra il lavoro (in Joule) necessario per
trasferire la carica elettrica, e la carica elettrica stessa (in Coulomb). V = J/C
La resistenza (R) che un conduttore offre al passaggio della carica dipende dal tipo di
sostanza, dalle sue dimensioni e dalla temperatura. L'unità pratica di resistenza è
l'ohm. La relazione tra potenziale, intensità di corrente e resistenza è data dalla
legge di Ohm, V = I R.
La velocità alla quale si effettua il lavoro elettrico è la potenza elettrica (W): la sua
unità pratica è il watt, che rappresenta la potenza in gioco quando un ampère circola
fra la differenza di potenziale di un volt (W = I V). W = J/s = V C/s = V A
Il lavoro elettrico è il prodotto della potenza elettrica per il tempo (t) in cui viene
impiegata: la sua unità pratica è il watt secondo, o joule, e rappresenta l'energia
fornita in un secondo da una corrente che impiega la potenza di un watt
(E = I V t = Q V).
Esercizio 1
L'intensità della corrente che passa in un conduttore è di 2,5 A.
Calcolare quanti coulomb passano nel conduttore in 1,4 minuti.
Esercizio 2
Se l’intensità della corrente che passa è 4,70 mA, quanto tempo viene richiesto per
ottenere 96500 C?
Pagina 1
BIC
Equilibrio di ossido-riduzione
2.
Reazioni di ossido riduzione
2.1
Dal concetto di Lavoisier a quello moderno
AS 2005/2006
Lavoisier introdusse il concetto di ossidazione per descrivere quei processi nei quali
una sostanza si combina con l'ossigeno.
L'espressione riduzione venne impiegata per ogni reazione nella quale a un composto si
toglieva ossigeno. Spesso il concetto di ossidazione e di riduzione venne associato a
processi di combustione.
Esistono tuttavia molte reazioni che esteriormente non differiscono in nulla dai tipici
processi di combustione, ma alle quali l'ossigeno non partecipa. Così, per esempio, il
sodio e l'alluminio riscaldati "bruciano" in presenza di cloro.
Si è quindi dimostrato conveniente estendere il concetto di ossidazione e riduzione, in
modo che esso possa essere usato anche per questi processi del tutto simili alle
combustioni tradizionali.
Secondo la teoria moderna, l'ossidazione è un processo nel quale una particella (atomo,
ione, molecola) cede degli elettroni mentre la riduzione è un processo nel quale una
particella acquista degli elettroni. Processi di ossidazione e di riduzione avvengono
sempre contemporaneamente. Il processo globale è un processo reversibile ed è detto
ossido-riduzione (o elettronolisi) e corrisponde a un trasferimento di elettroni.
Le particelle in grado di ossidare altre particelle sono dette ossidanti mentre quelle in
grado di ridurne altre sono dette riducenti.
Per riconoscere un processo di ossidoriduzione si fa ricorso ad un artificio: il numero
d’ossidazione (N.O.). Il N.O. è il numero di elettroni scambiati durante la formazione
di un legame. Porta sempre un segno: positivo per gli elettroni ceduti e negativo per gli
elettroni acquistati.
Poiché in una ossidazione una particella cede degli elettroni, il suo numero di
ossidazione (N.O.) aumenta mentre nel caso di una riduzione l'N.O. diminuisce. Nelle
reazioni di ossido-riduzione la variazione degli N.O. è nulla: ad ogni aumento
corrisponde sempre una diminuzione avente lo stesso valore assoluto.
Per assegnare il N.O. si fa riferimento alle seguenti regole:



Il N.O. degli atomi allo stato libero è sempre zero. Anche il N.O. degli elementi
allo stato molecolare (es. H2, O2, N2, Cl2,…) è zero.
Il N.O. dell’idrogeno è sempre +I (eccezione: idruri metallici del I e del II
gruppo come NaH e CaH2 dove è –I)
Il N.O. dell’ossigeno è sempre –II (eccezione: i perossidi come l’acqua
ossigenata, dove è –I)
Pagina 2
BIC
Equilibrio di ossido-riduzione
AS 2005/2006

Il N.O. dei metalli alcalini (I gruppo) è sempre +I; il N.O. dei metalli alcalino



terrosi (II gruppo) è sempre +II
In uno ione semplice il N.O. è uguale alla carica
Nei composti neutri la somma algebrica dei N.O. dei vari atomi è uguale a zero!
Negli ioni poliatomici come SO42- la somma algebrica dei N.O. dei vari atomi è
uguale alla carica dello ione.
Regola principale per assegnare il N.O.: controllare prima idrogeno e ossigeno
Per individuare un processo di ossidoriduzione basta verificare se durante una
reazione vi sono cambiamenti nel numero di ossidazione.
Se un elemento viene ossidato, il suo N.O. aumenta
Se un elemento viene ridotto, il suo N.O. diminuisce
Se in una reazione i N.O. non variano, la reazione non è una redox!
Esempi
2 H20 + O20
2 Na0 + Cl20
2 H2+IO-II
2 Na+ICl-I
Fe+IICl2-I + Ce+IVCl4-I
(H0 viene ossidato a H+I ; O0 viene ridotto a O-II)
(Na0 viene ossidato a Na+I ; Cl0 viene ridotto a Cl-I)
(Fe+II viene ossidato a Fe+III ;
Fe+IIICl3-I + Ce+IIICl3-I
Ce+IV viene ridotto a Ce+III)
Nota: siccome nella reazione tra FeCl2 e CeCl4 , gli ioni Cl- non partecipano al processo
di ossidoriduzione, questo può essere espresso nella forma semplificata seguente:
Fe+II + Ce+IV
Fe+III + Ce+III
Gli stati ridotto e ossidato di una particella (H+I/H0, Na+I/Na0) costituiscono una
coppia di ossido riduzione.
Nel processo di ossidoriduzione partecipano sempre (almeno) due coppie.
Esercizio 3
Per le seguenti reazioni, assegnare i numeri di ossidazione e, nel caso si tratti di una
reazione redox, indicare l’elemento che si riduce e quello che si ossida.

Sintesi dell’ammoniaca:
N2 + 3 H2
2 NH3
Pagina 3
BIC
2.2
Equilibrio di ossido-riduzione

Produzione di alcol metilico:

Fotosintesi:

SO3 + H2O
CO + 2 H2
6 CO2 + 6 H2O
AS 2005/2006
CH3OH
C6H12O6 + 6 O2
H2SO4
Ossido - Riduzione
Processi chimici che avvengono con trasferimento di elettroni "Elettronolisi"
perdita di elettroni (e-)
una particella, atomo neutro se cede e- diventa uno ione positivo
→si ossida
Ossidazione →
semireazione di ossidazione
2 Mg0  2 Mg+II + 4 eRiduzione
acquisto di elettroni (e-)
→
semireazione di riduzione
O20 + 4 e-  2 O2-II
Le 2 semireazioni sono contemporanee e questo processo si chiama Redox
2 Mg + O2  2 MgO
Schema
I. coppia
Red
Ox1 + e-
II. coppia
Ox
Red2
Redox
Ox1 + Red2
Red1
Ox2 + e-
Riduzione
Ossidazione
Red1 + Ox2
Pagina 4
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Ossidante = particella che prende e- (accettore di elettroni), ovvero si riduce
Riducente = particella che cede e-(donatore di elettroni), ovvero si ossida
Regola:
2.3
aumento di N.O.
diminuzione di N.O.
→
→
Ossidazione
Riduzione
Bilanciamento delle equazioni redox (di P. Lubini)
Il Bilanciamento delle equazioni di ossidoriduzione è assai complesso e generalmente
viene svolto in più passaggi. Il punto chiave comunque consiste nell’individuare le
semireazioni di ossidazione e di riduzione.
Bilanciare una redox:


Conservazione degli atomi (equivale alla conservazione della massa. Durante una
reazione chimica la massa si conserva e le sostanze si trasformano). Gli atomi si
conservano e si legano tra di loro in modo diverso (rottura e formazione di
legami).
Conservazione della carica elettrica! La somma dei numeri di ossidazione di
reagenti e prodotti deve essere uguale.
Metodo:






Identificare le specie che sono ossidate o ridotte (Numero di Ossidazione)
Scrivere separatamente le semireazioni dei processi d’ossidazione e di
riduzione.
Equilibrare ogni semireazione per rapporto agli atomi (eccetto ossigeno ed
idrogeno)
Equilibrare ogni semireazione per rapporto all’ossigeno, aggiungendo un numero
appropriato di molecole d’acqua alla parte carente di ossigeno
Equilibrare ogni semireazione per rapporto all’idrogeno aggiungendo un numero
appropriato di ioni H+ alla parte carente di idrogeno
Combina le reazioni di ossidazione e di riduzione in modo che gli elettroni
coinvolti si annullino
Nel caso in cui la reazione si svolga in ambiente basico, elimina ogni H +(aq) che compare
nell’equazione bilanciata combinandolo con OH-(aq) per dare H2O(l) (per ogni H+(aq)
aggiungi un OH-(aq) a destra e a sinistra dell’equazione bilanciata).
Pagina 5
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esempio
Equilibra la seguente reazione chimica in ambiente acido:
NO3- + S
SO2 + NO

Specie ossidata: S
Specie ridotta: NO3-
perde 4 elettroni ( N.O. da 0 a + IV)
acquista 3 elettroni (N.O. da +V a +II)

Semireazione di ossidazione:
S  SO2 + 4 e-
Semireazione di riduzione:
NO3- + 3 e-  NO

Equazioni già equilibrate per rapporto agli atomi (eccetto H e O)

Equilibrio per rapporto all’ossigeno:


Equilibrio per rapporto all’idrogeno:
S + 2 H2O  SO2 + 4 eNO3- + 3 e-  NO + 2 H2O
S + 2 H2O  SO2 + 4 e- + 4 H+
NO3- + 3 e- + 4 H+  NO + 2 H2O
Moltiplicare le semireazioni in modo che gli elettroni si annullino:
3x S + 2 H2O  SO2 + 4 e- + 4 H+ 
4x NO3- + 3 e- + 4 H+  NO + 2 H2O 
4NO3- + 3S + 4 H+
3 SO2 + 4 NO + 2 H2O
Esercizio 4
Equilibria la seguente reazione chimica che avviene in ambiente basico:
OH-
(aq)
Fe OH2 + CrO42- 
 Fe OH3 + Cr OH4

Equilibria le seguenti reazioni chimiche che avvengono in ambiente acido:
FeSO4 + MnO4- + SO42MnSO4 + Fe2 SO4 3
Cu + NO3-
NO + Cu NO3 2
Pagina 6
BIC
2.4
Equilibrio di ossido-riduzione
AS 2005/2006
Criteri di spontaneità per una reazione redox (di P. Lubini)
I criteri qui di seguito elencati sono di carattere qualitativo:

Numero di ossidazione (N.O.)
Un ossidante (composto/elemento che ossida – che ha quindi fame di elettroni – e
che si riduce) ha un numero di ossidazione elevato per rapporto al suo N.O.
preferito (che dipende dal posto occupato nella tavola periodica).
Un riducente (composto/elemento che riduce – ha cioè troppi elettroni e vuole
liberarsene – e che quindi si ossida) ha un numero di ossidazione basso per
rapporto al suo N.O. preferito (che dipende dal posto occupato nella tavola
periodica).

Tavola periodica
Dall’analisi dell’energia di ionizzazione ad affinità elettronica abbiamo ottenuto una
preziosa guida per capire il legame chimico: gli atomi tendono a raggiungere una
configurazione elettronica possibilmente uguale a quella del gas nobile più prossimo
sulla tavola periodica.
Per raggiungere questo obbiettivo, alcuni atomi tenderanno a perdere elettroni
(metalli) ed altri ad acquistarli (non-metalli). La classificazione del legame chimico
INTRAMOLECOLARE (tra atomi appartenenti alla stessa molecola) avviene sulla
base delle modalità secondo la quale gli atomi condividono gli elettroni che formano
il legame chimico. In tale contesto uno strumento estremamente utile per la
classificazione dei legami si è rivelato essere l’elettronegatività (tendenza relativa
di un atomo ad attrarre gli elettroni). Maggiore elettronegatività e maggiore è il
potere ossidante.
Pagina 7
BIC

Equilibrio di ossido-riduzione
AS 2005/2006
Serie di reattività dei metalli
Come visto i metalli hanno tendenza ad ossidarsi (cedere elettroni ai non-metalli).
Non tutti i metalli mostrano però la medesima tendenza: ve ne sono di più o meno
reattivi (sempre a seconda della posizione nella tavola periodica). Una classifica
viene stilata in base alla reattività per rapporto ad aria (ossigeno) ed acqua
secondo le seguenti reazioni generali:
Metallo + ossigeno  Ossido di metallo (basico)
Metallo + acqua  Idrossido + Idrogeno gassoso
Esercizio 5
Classifica i seguenti composti come possibili ossidanti o riducenti:
Ammoniaca, metano, ossigeno, acqua ossigenata, sodio, ferro, fluoro, cloro neon,
permanganato di potassio (KMnO4), dicromato di potassio (K2Cr2O7).
Esercizio 6
Come ti spieghi il fatto che pochi metalli (quali?) in natura sono presenti allo stato
elementare?
Esercizio 7
Prova a prevedere quale delle seguenti reazioni probabilmente avverrà e quale no.
Argomenta la tua risposta!
Mg + CuO  Cu + MgO
Fe + Na2O  Na + FeO
Esercizio 8
Formula l’equazione del calcio con l’acqua e del potassio con l’ossigeno
Esercizio 9
In base alla tua conoscenza della tavola periodica qual è l’elemento più ossidante e
quale quello più riducente?
Pagina 8
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esercizio 10
Secondo te quale tra gli ioni Cu2+ e Zn2+ sarà il miglior ossidante (avrà cioè la maggior
tendenza a ridursi – acquistare elettroni)? Perché?
Esercizio 11
L’acqua ossigenata può essere usata come antisettico. Un campione di soluzione di
questa sostanza di massa 1,0 g viene titolato con una soluzione di KMnO 4 0,2 M.
L’equazione (da bilanciare) è la seguente:
H2O2 + MnO4-  O2 + Mn2+
(ambiente acido)
La titolazione ha richiesto 16,6 mL di permanganato di potassio.
a) Quanti grammi di acqua ossigenata hanno reagito?
b) Qual è la % m/m di H2O2 nella soluzione?
3.
Elettrochimica I
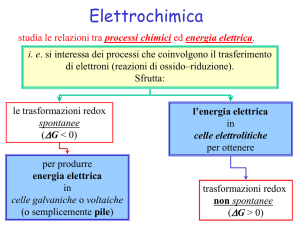
L'elettrochimica studia le relazioni che esistono tra i processi chimici e l'energia
elettrica. Essa può essere divisa in due aree generali sostanzialmente l'una l'inverso
dell'altra, ma governate da principi comuni:
 processi chimici ossido-riduttivi che avvengono spontaneamente possono, in
opportune condizioni, essere sfruttati come fonti d'energia elettrica,
 processi chimici che non potrebbero avvenire spontaneamente possono essere
realizzati fornendo, in particolari condizioni, energia elettrica.
I dispositivi elettrochimici sedi di processi chimici spontanei (∆G < 0) sono chiamati
celle galvaniche o pile, quelli sedi di processi chimici non spontanei (∆G > 0) sono
chiamati celle elettrolitiche.
Nell'ambito comune di queste due aree vi sono aspetti teorici e pratici che vanno
sottolineati.
Dal punto di vista strettamente chimico o teorico, mediante le celle galvaniche è
possibile condurre i processi ossido-riduttivi in condizioni di reversibilità
termodinamica: ciò consente di calcolare il lavoro massimo possibile (di tipo elettrico)
e, quindi, di misurare quantitativamente la spontaneità (∆Greaz) di una reazione nonché
il rapporto prodotti/reagenti nelle condizioni proprie dell'equilibrio (Keq). Mediante le
celle elettrolitiche è invece possibile studiare il trasporto della carica elettrica nei
sistemi chimici.
Dal punto di vista pratico, mediante le conoscenze dell'elettrochimica è possibile
ideare e costruire celle galvaniche e batterie che danno corrente elettrica in piccole
quantità nei luoghi più convenienti, oppure costruire celle elettrolitiche che
Pagina 9
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
consentono l'elettrodeposizione, la raffinazione e la produzione di importanti metalli,
oppure utilizzare sistemi elettrochimici per bloccare la corrosione dei metalli.
3.1
Principi della pila chimica
Se una barretta di Zn metallico viene immersa in una soluzione contente ioni Ag+, dopo
un certo tempo, si può notare che la superficie della barretta a contatto con la
soluzione si è ricoperta di un sottile strato di Ag metallico e che nella soluzione sono
presenti, oltre a una parte di ioni Ag+ iniziali, anche ioni Zn2+
Questo fenomeno è rappresentato dalla reazione redox:
Zn + 2 Ag+(aq)  Zn2+(aq) + 2 Ag
somma delle due semireazioni d'ossidazione (Zn  Zn2+(aq) + 2 e-) e di riduzione
(2 Ag+(aq) + 2 e-  2 Ag) in cui gli elettroni vengono trasferiti in modo diretto e
disordinato dallo Zn metallico agli ioni Ag+ .
La reazione avviene spontaneamente (Greaz < 0) ed è esoterminca (Hreaz < 0): quando
una mole di Zn metallico ha reagito completamente con 2 moli di ioni Ag+, alla
temperatura di 25°C e pressione 1 atm, la quantità d'energia che viene liberata dalla
reazione come calore può essere facilmente misurata, per esempio, mediante un
calorimetro (∆Hreaz = -87000 cal).
Se la stessa reazione, anziché farla avvenire in un calorimetro, viene condotta in un
dispositivo elettrochimico, chiamato cella galvanica o pila, è possibile sfruttare gran
parte dell'energia libera (∆Greaz) e trasformarla in lavoro elettrico (Wel), cioè in
energia elettrica.
La cella galvanica o pila è un dispositivo che permette alle due semireazioni di
ossidazione (Zn  Zn2+(aq) + 2 e-) e di riduzione (2 Ag+(aq) + 2 e-  2 Ag) d'avvenire
contemporaneamente ma separatamente, e agli elettroni di essere trasferiti in modo
ordinato ma indiretto dal riducente (Zn metallico) all'ossidante (ioni Ag +) attraverso
un circuito esterno dal quale è possibile prelevare energia elettrica.
È possibile realizzare una pila facendo avvenire le due semireazioni di cui si compone
la reazione redox in due distinti scomparti, chiamati semielementi. In questo caso
ciascun semielemento deve contenere una barretta del metallo immersa in una
soluzione dei suoi ioni: l'uno Zn metallico e ioni Zn2+, l'altro Ag metallico e ioni Ag+.
Tra metallo e soluzione si crea una differenza di potenziale (V), chiamata potenziale
di semielemento, il cui valore assoluto non può essere misurato sperimentalmente.
Naturalmente non ci sarà reazione fino a quando gli elettroni non potranno essere
trasferiti da un semielemento all'altro. Se le due barrette di Zn e Ag vengono
Pagina 10
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
collegate con un conduttore metallico (p.e. del filo di rame) è possibile, per un istante,
il passaggio degli elettroni dal semielemento i cui avviene la semireazione
d'ossidazione (Zn  Zn2+(aq) + 2 e-) a quello in cui avviene la semireazione di riduzione
(2 Ag+(aq) + 2 e-  2 Ag).
A parità di condizioni, il semielemento di Zn assume polarità negativa rispetto al
semielemento di Ag che assume, quindi, polarità positiva.
Per rendere continuativo il trasferimento degli elettroni dal polo negativo al polo
positivo, occorre che le soluzioni nei due semielementi siano a contatto fra di loro: se
le soluzioni vengono collegate con un conduttore elettrolitico (ponte salino) gli ioni
possono migrare da un semielemento all'altro e compensare lo squilibrio di cariche
ioniche provocato dalle semireazioni d'ossidazione e di riduzione.
In questo modo si realizza un circuito continuo attraverso cui particelle cariche
possono fluire: il passaggio ordinato d'elettroni nel filo conduttore esterno è corrente
elettrica, la migrazione degli ioni tramite il contatto liquido assicura
l'elettroneutralità in ogni punto del sistema e la reazione che si compie "a distanza"
nei due semielementi è il processo elettromotore.
La differenza di potenziale (d.d.p.) che si manifesta tra i due semielementi può essere
misurata inserendo un opportuno strumento (voltmetro) nel circuito esterno e
Pagina 11
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
l'energia elettrica prodotta dal movimento degli elettroni può essere utilizzata per
compiere lavoro utile, nel nostro caso lavoro elettrico (Wel).
Man mano che la reazione redox procede, le attività delle specie ioniche presenti nelle
soluzioni variano tendendo, con il tempo, all'equilibrio e la d.d.p. della pila diminuisce
progressivamente: ad equilibrio raggiunto la reazione s'arresta, la d.d.p. s'annulla e la
pila non è più in grado d'erogare energia elettrica.
La massima d.d.p. di una pila, chiamata forza elettromotrice (f.e.m., Epila), non viene
misurata a circuito chiuso bensì a circuito aperto, ovvero a passaggio di corrente nullo.
Per misurare la f.e.m. della pila nelle condizioni d'attività scelte, al posto del
voltmetro s'inserisce un potenziometro che è lo strumento di misura della d.d.p.
quando nel circuito esterno non passa corrente.
In queste condizioni il processo elettromotore avviene in modo reversibile e il lavoro
elettrico fornito dalla pila è il massimo ottenibile e misura esattamente la variazione
d'energia libera che accompagnerebbe lo svolgersi della reazione redox (∆Greaz).
Prima d'addentrarci negli aspetti quantitativi delle relazioni tra energia elettrica,
reazioni chimiche e variazione d'energia libera, vediamo d'illustrare brevemente i
termini e le grandezze elettriche che comunemente vengono usate e la loro
derivazione:
Grandezza elettrica
Simbolo
Unità di misura
Simbolo
Carica
Q
coulomb
C
Intensità
Resistenza
d.d.p. , f.e.m.
Potenza
Energia, lavoro
I
R
E
P
W
ampère
ohm
volt
watt
joule
A
Ω
V
W
J
interrelazioni
(*)
I = Q/t
R = E/I
E=I R
P=E I
W=E Q
(*)
Poiché la quantità d'elettricità trasportata dalla carica elementare, cioè da 1
elettrone, è 1.60 10-19 C, 1 coulomb rappresenta la quantità d'elettricità trasportata
da 6,25 1018 elettroni, 1 faraday rappresenta la quantità d'elettricità trasportata da
6,02 1023 elettroni, cioè da 1 mole di elettroni.
1 Faraday = 1.60 10-19 C/e- 6,02 1023 e-/mol e- = 96487 C/mol eQuesto valore viene arrotondato a 96500 per comodità di calcolo.
Pagina 12
BIC
3.2
Equilibrio di ossido-riduzione
AS 2005/2006
Conduttori
La conduzione della corrente elettrica avviene principalmente per mezzo di due tipi di
conduttori:
conduttori metallici (o elettronici) nei quali la conduzione è dovuta al flusso orientato
di elettroni liberi che percorrono il conduttore. Il passaggio di corrente ha luogo
senza trasporto di materia in quanto sono gli elettroni che trasportano le cariche
elettriche (corrente elettronica). Sono conduttori di questo tipo i metalli puri, le
leghe metalliche, la grafite ed alcuni ossidi e sali particolari.
Per essi il passaggio di corrente continua avviene quando si applica una differenza di
potenziale E comunque piccola, secondo la legge di Ohm: I = E/R.
Conduttori elettrolitici (o ionici) nei quali la conduzione è dovuta al moto orientato di
ioni liberi di muoversi all'interno del conduttore.
Il passaggio di corrente è accompagnato da trasporto di materia in quanto gli ioni sono
le particelle materiali che trasportano le cariche elettriche (corrente ionica).
Sono conduttori di questo tipo le soluzioni elettrolitiche (acidi, basi e sali in solventi
acquosi e polari), i sali fusi, alcuni liquidi puri ed alcuni solidi cristallini.
Per essi il passaggio di corrente continua è apprezzabile solo quando la differenza di
potenziale applicata supera un certo valore di soglia Ed caratteristico di ciascuno e la
legge di Ohm viene seguita nella forma I = (E - Ed)/R .
I conduttori elettrolitici seguono la legge di Ohm classica quando sono percorsi da
corrente alternata di frequenza sufficientemente elevata da poter escludere i
fenomeni di polarizzazione (migrazione e scarica degli ioni) che alterano le condizioni
del trasporto ionico.
3.3
Semielementi – Potenziale di semielemento – Equazione di Nernst
Un semielemento è costituito da un elettrodo
(conduttore metallico: metallo o grafite) a contatto
con un elettrolita (conduttore elettrolitico:
elettrolita in soluzione o fuso).
Tra elettrodo ed elettrolita si stabilisce una
differenza di potenziale originata dall'equilibrio
all'interfase tra la forma ossidata (ox) e ridotta
(red) del sistema ossido-riduttivo che costituisce un
semielemento:
 ox + n e-
 red
Pagina 13
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
La capacità degli elettroni di trasferirsi da una forma all'altra o viceversa è una
caratteristica di ogni sistema ossido-riduttivo e viene misurata dal suo potenziale.
Poiché ogni sistema ossido-riduttivo costituisce formalmente, in opportune condizioni,
un semielemento, i potenziali misurati sono anche i potenziali di semielemento.
L'equazione di Nernst fornisce il mezzo per la trattazione quantitativa ed il calcolo
dei potenziali di semielemento nelle condizioni d'attività, pressione e temperatura
scelte.
A 25°C ed 1 atm per la semireazione generica  ox + n e red , la variazione
d'energia libera ∆G è in relazione sia con il grado d'avanzamento della stessa che con
il lavoro utile da essa ottenibile. Una forma di lavoro utile è quello elettrico definito
come prodotto della quantità d'elettricità (Q, coulomb) per la differenza di
potenziale (E, volt); se E esprime il potenziale del semielemento sede della generica
semireazione di cui sopra, F la quantità d'elettricità trasportata da una mole di
elettroni ed n il numero di elettroni scambiati, n F è la quantità d'elettricità
associata alla stechiometria della semireazione, e n F E rappresenta il lavoro
elettrico corrispondente.
Poiché:

red
a
G = G° + R T ln red
 G° + R T ln 

aox
ox
e per quanto detto:
G = - n F E
sostituendo opportunamente e cambiando segno, si ottiene:


G
G°
R T ared
G°
R T red
=
+
ln  
+
ln
-n F
-n F
-n F aox
-n F
-n F
ox
G°
è costante in tutte le condizioni, viene indicato con E° e chiamato
-n F
potenziale standard, per cui:
Il termine


R T ared
R T red
RT
ox
E = E° +
ln   E° +
ln

E°
+
ln

-n F aox
-n F
n F red
ox
Quindi, sia la variazione d'energia libera ∆G che il potenziale di semielemento E sono
una misura quantitativa della tendenza che il sistema ossido-riduttivo corrispondenze
ha ad evolversi quando interagisce con un altro sistema.
Pagina 14
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Sostituendo gli appropriati valori alla temperatura costante di 25°C (T = 298 K, R =
8,31 C V mol-1K-1 , F = 96500 C(mol e-)-1 , n = mol e- , ln  2,3 log) si ha:
RT
0,059
ln =
log
nF
n
Sostituendo si ottiene l’equazione di Nernst da utilizzare per il calcolo dei potenziali
di semielemento nelle condizioni d’attività scelte:
a
0, 059
0, 059
ox
E = E° +
log ox  E° +
log

n
ared
n
red

Dall’equazione di Nernst emerge quanto segue:
0, 059
 il rapporto
risulta espresso in volt: il simbolo n è quello di un numero
n
dimensionale che coincide con il numero di moli di elettroni scambiati; di
conseguenza il potenziale è una grandezza intensiva;
 il potenziale E di un semielemento dipende dal suo potenziale standard E°, dal
numero di lettroni in gioco n, e dalle attività a (per noi dalle concentrazioni
espresse in M) delle specie chimiche che prendono parte al processo ossidoriduttivo;
 il temrine logaritmico è un valore calcolabile note le concentrazioni delle specie


presenti. Viceversa, noti E ed E° è possibile determinare i valori delle
concentrazioni o il loro rapporto;
se per un qualsiasi semielemento risulta [ox] = [red] = 1 M, il termine
logaritmico si annulla e si ha E = E°. Il potenziale standard E° rappresenta
quindi il valore del potenziale del generico semielemento quando le
concentrazioni delle specie presenti sono unitarie;
il potenziale standard E° deve pertanto essere misurato sperimentalmente.
Poiché la misura diretta del potenziale di un semielemento è impossibile, è
necessario assumere un semielemento di riferimento, quello standard ad
idrogeno, e assegnare ad esso convenzionalmente potenziale uguale 0,00 V: il
valore del potenziale di un qualsiasi altro semielemento si può allora desumere
dal valore determinato sperimentalmente della f.e.m. della pila ottenuta
accoppiando il semielemento standard considerato e quello standard di
riferimento.
Pagina 15
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
3.4
Potenziale Standard di semielemento (E°) – Scala dei potenziali Standard
Se il potenziale E di semielemento è una misura della tendenza degli elettroni a
trasferirsi da una specie all’altra e questa tendenza dipende dalle concentrazioni delle
specie chimiche presenti, è conveniente per confrontare il potere ossido-riduttivo di
ciascun sistema far riferimento ad un particolare valore di queste concentrazioni.
La scala dei Potenziali, che riunisce i valori dei potenziali dei diversi sistemi ossidoriduttivi (v. Tabella), è basata sulle seguenti convenzioni:
1. i valori tabulati si riferiscono alle semireazioni in soluzione acquosa
considerate nel senso della riduzione: forma ossidata (ox) + n eforma
ridotta (red) e costituiscono una scala di potenziali di riduzione, cioè di forza
ossidante dei diversi sistemi; ciascun sistema è in grado di ridurre qualsiasi
sistema che lo segue e di ossidare qualsiasi sistema che lo precede;
2. i lavori non sono assoluti ma relativi al
potenziale del sistema ossido-riduttivo
H3O+/H2 di riferimento scelto ed
all'equilibrio
2 H3O+(aq) + 2 eH2 (g) + 2 H2O(l)
che si stabilisce nel semielemento a
idrogeno alla temperatura di 25°C quando
l'attività degli ioni H3O+(aq) è unitaria (per
i gas l'attività viene assunta unitaria alla
pressione p = 1 atm). Questo semielemento
di riferimento è detto standard o normale
ed il suo potenziale è convenzionalmente
posto uguale a 0,00 V in queste condizioni;
3. i valori si riferiscono alla temperatura di 25°C ed alla situazione d'attività
unitaria di tutte le specie (solide, ioniche o gassose) coinvolte nella
semireazione. Questi potenziali sono detti "standard o normali", si indicano con
il simbolo E° e sono caratteristici dei sistemi ossido-riduttivi.
Esercizio 12
Il potenziale del semielemento standard di Cu viene determinato sperimentalmente
accoppiando tale semielemento con un semielemento standard di H2 e misurando la
f.e.m. della pila ottenuta. Sapendo che la f.e.m. ∆E° = 0,337 V e che durante il
funzionamento della pila ioni Cu2+ danno luogo alla formazione di Cu metallico,
determinare il potenziale standard del semielemento di Cu.
Pagina 16
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esercizio 13
Il potenziale del semielemento standard in Zn viene determinato accoppiando tale
semielemento con un semielemento standard di H2 e misurando la f.e.m. della pila
ottenuta. Sapendo che la f.e.m. ∆E° = 0,763 V e che durante il funzionamento della
pila Zn metallico dà luogo a ioni Zn2+, determinare il potenziale standard del
semielemento di Zn.
Esempio
Una pila chimica è costituita da un semielemento standard di Cu e da un semielemento
standard di Ag. Il flusso di elettroni nel circuito esterno avviene dal semielemento di
Cu a quello di Ag. Sapendo che la f.e.m. misurata è 0,462 V, determinare il valore del
potenziale standard del semielemento di Ag, noto che E°Cu2+/Cu = 0,337 V .
Se il flusso degli elettroni è dal semielemento di Cu a quello di Ag, significa che nella
pila avvengono le seguenti semireazioni:
(-)
Cu

Cu2+(aq) + 2 e-
(+)
2 Ag+(aq) + 2 e-
E°Cu2+/Cu = 0,337 V

2 Ag
E°Ag+/Ag =
Cu + 2 Ag+

Cu2+(aq) + 2 Ag
?
V
La f.e.m. della pila in condizioni standard è:
E°pila = E°Ag+/Ag - (0,337) = 0,462 V
Da cui si ricava che:
E°Ag+/Ag = 0,462 + 0,337 = 0,799 V
Osservazione
Come si può notare, il potenziale standard di un semielemento può essere determinato
accoppiandolo con un qualsiasi semielemento a potenziale standard noto: per questo
scopo vi sono semielementi di riferimento a potenziale noto quale quello a calomelano
(Hg2Cl2/Hg) che è molto più pratico e facile da utilizzare di quanto sia il semielemento
a idrogeno (H3O+/H2).
3.5
Forza elettromotrice di una pila
Come si è visto ad ogni semireazione di riduzione è possibile associare una grandezza,
misurata in volt, chiamata potenziale di riduzione (Ered oppure E°red). Analogamente ad
Pagina 17
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
ogni semireazione di ossidazione è possibile associare una grandezza, misurata in volt,
detta potenziale di ossidazione (Eox oppure E°ox) il cui valore è uguale ma di segno
opposto a quello del potenziale di riduzione.
Poiché al polo negativo (-) di una pila avviene la semireazione di ossidazione e al polo
positivo (+) avviene la semireazione di riduzione, la f.e.m. della pila, sede della reazione
di ossido-riduzione, è data dalla somma dei potenziali di riduzione e di ossidazione.
Nel caso della pila standard Zn - Cu, per esempio, si ha:
polo pos (+):
polo neg (-)
Cu2+(aq) + 2 eZn
Cu2+(aq) + Zn

Cu

Zn2+(aq)

Cu + Zn2+(aq)
+2e
-
E°red = 0,337 V
E°ox = - E°red = -(-0,763 V)
E°pila = E°red + E°ox
Essendo E°ox = - E°red, la f.e.m. di una pila è ricavabile anche facendo la differenza tra
il potenziale di riduzione associato alla semireazione che avviene al polo positivo (E +red)
e il potenziale di riduzione associato alla semireazione che avviene al polo negativo
(E-red):
E°pila = E° +red + E° - ox= E° +red - E° - red
Quindi, per una generica pila in condizioni diverse da quelle standard possiamo
scrivere:
f.e.m. = Epila = Ered + Eox = E +red - E - red
Negli esercizi che seguono, quando non specificato diversamente, si fa riferimento
sempre ai potenziali di riduzione.
3.6
Significato dei Potenziali Standard
La capacità di un sistema ossido-riduttivo di comportarsi da agente ossidante o
riducente è in diretta relazione con il suo potenziale standard.1
Poiché i potenziali standard E° tabulati sono potenziali di riduzione, essi forniscono
una misura della tendenza di una semireazione a compiersi nella direzione che
corrisponde ad una riduzione, quindi, quanto più il potenziale standard E° è positivo,
tanto più il sistema ossido-riduttivo si comporta come agente ossidante.
1
Un sistema ossido-riduttivo non è di per sè un ossidante o un riducente ma assume l’una o l’altra capacità quando
viene confrontato con un altro sistema ossido-riduttivo
Pagina 18
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
I potenziali più positivi appartengono alle semireazioni in cui i migliori agenti ossidanti
si riducono: per esempio E°F /F- = 2,85 V indica che il fluoro (F2) è l'agente ossidante
2
per eccellenza ed anche la specie più facilmente riducibile (a ione F-); E°Cl /Cl- = 1,36 V
2
indica che il cloro (Cl2) è pure un buon agente ossidante, ma meno del fluoro.
Viceversa, quanto più il potenziale standard E° è negativo, tanto più il sistema ossidoriduttivo si comporta da agente riducente.
I potenziali più negativi appartengono alle semireazioni in cui i migliori agenti riducenti
si ossidano: per esempio, E°Li+/Li = - 3,05 V indica che lo ione Li+ è un agente ossidante
molto debole che si riduce con estrema difficoltà a Li metallico, invece Li metallico è il
migliore agente riducente ed anche la specie più facilmente ossidabile (a ione Li +);
E°Mg2+/Mg = - 2,37 V indica che anche Mg met. è un buon agente riducente, ma meno di
Li met.
Possiamo così riassumere quanto detto:
Li+ + e-
F2 + 2e -
Li
2F-
EF0/F- = 2,85 V
ELi0+/Li = - 3,05 V
2
- potenziale standard più negativo;
- semireazione con la minore tendenza
procedere come riduzione;
- Potenziale standard più positivo;
- semireazione con la maggiore
tendenza a procedere come
riduzione;
- Li+ è il peggior agente ossidante;
- la semireazione inversa (ossidazione)
ha la maggiore tendenza a compiersi;
- F2 è il miglior agente ossidante;
- la semireazione inversa
(ossidazione) ha la minore
tendenza a compiersi;
- F- è il peggior agente riducente.
- Li è il miglior agente riducente;
3.7
Utilizzo dei Potenziali Standard
La scala dei potenziali standard consente di:
- stabilire la direzione in cui una reazione di ossido-riduzione è spontanea e di
calcolarne la costante di equilibrio (Keq);
- calcolare il valore del potenziale di un semielemento in condizioni non standard
mediante l'equazione di Nernst e, di conseguenza, di stabilire il potere ossidante o
riducente di un sistema ossido-riduttivo al variare delle condizioni sperimentali;
- calcolare i valori dell'energia libera molare standard di formazione ( ΔGf0 ) delle
varie specie ioniche in soluzione difficilmente determinabili per altra via;
Pagina 19
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
- calcolare, mediante i potenziali di semielemento misurati sperimentalmente, i valori
delle attività delle specie chimiche coinvolte presenti in soluzioni e, quindi, del pH
di una soluzione, del prodotto di solubilità (KPS) di sali poco solubili, della costanze
d'instabilità di uno ione complesso, ...;
- stabilire, a priori, il valore della forza elettromotrice (f.e.m.) di una pila ottenuta
accoppiando opportunamente due qualsiasi semielementi, siano essi standard o non;
- calcolare la quantità massima di lavoro elettrico ottenibile da una reazione di
ossido-riduzione (o non) fatta avvenire in una pila;
- calcolare il lavoro elettrico necessario per far avvenire una reazione di ossidoriduzione non spontanea in una cella elettrolitica.
3.8
Relazione tra ΔE0 e ΔG 0
Previsione della spontaneità di una reazione di ossido-riduzione
Tra la variazione d'energia libera (∆G) che accompagna lo svolgersi di una reazione di
ossido-riduzione e la f.e.m. positiva (∆E) che essa genera in condizioni di reversibilità
termodinamica sussiste la relazione: ΔG = - n F ΔE
È di particolare interesse l'applicazione di questa relazione quando i reagenti ed i
prodotti si trovano in condizioni standard; in tali condizioni si può scrivere:
ΔG° = - n F ΔE° , dove ∆G° è la variazione d'energia standard e ∆E° è la f.e.m.
standard.
Poiché ∆G° rappresenta una misura della tendenza di una reazione ad avvenire
spontaneamente in condizioni standard, ∆E° associata ad una reazione di ossidoriduzione è, a sua volta, un criterio di spontaneità.
Se:
∆G° < 0 ,
∆G° > 0 ,
∆E° > 0
∆E° < 0
reazione spontanea così come scritta;
reazione non spontanea (è spontanea la reazione
inversa)
Questo è un risultato interessante, poiché in base ad esso è evidentemente possibile
misurare le costanti d'equilibrio partendo dai potenziali della cella quando le costanti
di equilibrio sono troppo grandi o troppo piccole per essere misurate per mezzo di
analisi dirette di una miscela all'equilibrio.
Dovrebbe essere ugualmente evidente che se sono disponibili i dati dell'energia libera
derivanti da altri fonti come misura diretta delle variazioni d'entropia ed entalpia di
reazione, allora può essere calcolato l'E° della reazione e indirettamente quello della
semireazione della tabella dei potenziali.
Pagina 20
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esaminando la tabella dei potenziali di riduzione troviamo che essi variano da circa +3
a -3 V. Una differenza di 6 V nei potenziali di una reazione corrisponde ad una
costante di equilibrio di 10100n, dove n è il numero di elettroni trasferiti in un processo
redox.
Infatti
0,059
E° =
log Keq
6,0
n
log Keq  100n
Keq  10100n
3.9
Applicazioni dei potenziali di riduzione
In numerosi casi i potenziali di riduzione permettono di prevedere la possibilità di
reazione tra particelle diverse.
3.9.1 Azione di un elemento sugli ioni di un altro elemento
Quando si immerge un metallo in una soluzione contenente gli ioni di un altro metallo
con potenziale di riduzione maggiore, il metallo si dissocia mentre su questo si
scaricano gli ioni della soluzione.
Esempio
Ferro immerso in una soluzione contenente ioni Cu2+
Fe + Cu2+ →Cu + Fe2+
Rame immerso in una soluzione contenente ioni Ag+
Cu + 2 Ag+ →Cu2+ + 2 Ag
Nota: ovviamente le reazioni inverse non si realizzano.
3.9.2 Reazioni dei metalli con acidi
L'attacco di un metallo da parte di un acido è un metodo di preparazione dell'idrogeno.
Si possono impiegare tutti i metalli il cui potenziale di riduzione è minore di quello
dell'idrogeno.
La reazione
n
H2
2
è tanto più forte quanto minore è il potenziale di riduzione del metallo.
Esempio
2 HCl(aq) + Zn →ZnCl2 (aq) + H2 (g)
E°Zn2+/Zn = - 0,76 V
n H3O+ + Me →Men+ + n H2O +
Pagina 21
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Gli ossiacidi più ossidanti attaccano anche i metalli con potenziale maggiore di zero. In
questo caso però non si sviluppa H2 ma si forma un composto di ossigenato del non
metallo avente un numero di ossidazione inferiore.
Esempio
3 Cu + HNO3 (diluito) →3 Cu(NO3)2 + 4 H2O + 2 NO
E°Cu2+/Cu = 0,34 V
E°NO-/NO = 0,94 V
3
3.9.3 Reazione dei metalli con l'acqua
L'acqua si dissocia molto debolmente secondo l'equilibrio
2 H2O
H3O+ + OHGli ioni H3O+ reagiscono con un metallo
n
H2
2
Come nel caso precedente, la reazione è tanto più forte quanto minore è il potenziale
di riduzione del metallo.
L'equazione globale della reazione è
n
n H2O + Me →Me(OH)n +
H2
2
Ovviamente i metalli il cui potenziale di riduzione è maggiore di zero non reagiscono
con l'acqua
Esempio
E°Na+/Na = - 2,71 V
2 H2O + 2 Na →2 NaOH + H2
n H3O+ + Me →Men+ + n H2O +
2 H2O + Ca →Ca(OH)2 + H2
E°Ca2+/Ca = - 2,87 V
3.9.4 Reattività dei metalli
I metalli con potenziale di riduzione maggiore di zero sono tanto più ineri quanto
questo potenziale è grande. Questo è il motivo per cui i metalli cosiddetti nobili (Pt,
Au, Ag) non sono attaccati dall'ossigeno a temperatura ambiente.
3.9.5 Protezione contro la corrosione dell'acciaio
La corrosione del ferro è un processo redox. Quando del ferro metallico viene
ossidato, vengono ridotti sia l'ossigeno gassoso che gli ioni idronio, con formazione di
ioni Fe2+ e di OH- o H2
Fe(s)  Fe2+ + 2 e (a)
1
O2 (g) + H2O + 2 e-  2 OH 2
2 H3O+ + 2 e -  2 H2O + H2 (g)
Pagina 22
(b)
(c)
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Una protezione contro la corrosione può essere effettuata ricoprendo la superficie
con un rivestimento di qualche specie (pittura, per esempio). Si può raggiungere una
migliore protezione se nel rivestimento si tiene conto dell'elettrochimica: una
superficie di ferro può per esempio essere costretta a comportarsi da catodo invece
che da anodo, come nell'equazione (a), creando una cella elettrochimica con un metallo
a più basso E°. Un esempio è l'acciaio galvanizzato.
Il rivestimento di zinco agisce come anodo, facendo diventare il ferro il catodo.
Anodo: ossidazione
Zn  Zn2+ + 2 e-
E°ox = + 0,76 V
Catodo: riduzione
Fe
E°red = - 0,44 V
2+
+ 2 e  Fe
-
Il potenziale della cella è
E°cella = E°catodo - E°anodo = (-0,44) – (-0,76) = 0,32 V
Quindi la reazione spontanea è
Zn + Fe2+  Zn2+ + Fe
che evita l'ossidazione del ferro nell'acciaio.
Un pezzo di magnesio sotterrato in luogo paludoso, può essere collegato a un oleodotto
sotterraneo e, agendo come anodo, proteggere l'acciaio ossidandosi esso stesso. Le
semireazioni sono:
Mg2+ + 2 e-  Mg
E° = - 2,37 V
Fe2+ + 2 e-  Fe
E° = - 0,44 V
Queste portano alla reazione totale
Mg + Fe2+  Mg2+ + Fe
E°cella = E°catodo - E°anodo = (-0,44) – (-2,37) = 1,93 V
Il magnesio usato a questo scopo viene detto metallo di sacrificio. Blocchi di magnesio
attaccati allo scafo di una nave in navigazione hanno la stessa funzione.
Questo criterio trova vasta applicazione generale allorché si vuole stabilire se una
reazione di ossido-riduzione può avvenire o meno spontaneamente in condizioni
standard.
Per usare nella pratica le relazioni di cui sopra occorre tener presente quanto segue:
a) il valore del potenziale standard di una semireazione, essendo una proprietà
intensiva, non dipende dalla quantità delle sostanze coinvolte, cosicché
moltiplicando la semireazione per un coefficiente numerico positivo il valore di E°
non cambia;
b) il segno dei valori dei potenziali standard s'inverte quando le semireazioni
considerate sono scritte nella direzione opposta, cioè nel senso dell'ossidazione;
Pagina 23
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
c) essendo una reazione di ossido-riduzione la somma di due semireazioni, la f.e.m.
standard può essere vista come la somma dei potenziali standard relativi alla
semireazione d'ossidazione (E°ox) e di riduzione (E°red);
d) ∆E° rappresenta una misura quantitativa della tendenza dei reagenti nel loro stato
standard a passare a prodotti nel loro stato standard.
Esercizio 14
Prevedere se Al metallico può spostare ioni Cu2+ da una soluzione acquosa:
2
2 Al + 3 Cu(aq)
3
2 Al(aq)
+ 3 Cu
E°Al3+/Al = -1,66 V ; E°Cu2+/Cu = 0,34 V
Nota: Significa accertarsi se questa reazione può avvenire spontaneamente così come
scritta
Esercizio 15
Verificare se le seguenti reazioni di disproporzione possono avvenire in condizioni
standard:

2
a)
2 Cu(aq)
Cu(aq)
+ Cu
b)
noti E°Cu
2+
/Cu+
Hg22(aq)
2
Hg(aq)
+ Hg(l)
= 0,15 V; E°Cu /Cu = 0,52 V; E°Hg
+
2+
/Hg22+
= 0,92 V; E°Hg
2+
2 /Hg
= 0,79 V
Esercizio 16
Verificare se 02 gassoso può ossidare Au ad Au(CN)2- in presenza di ioni cianuro (CN-),
noti i potenziali standard E°Au(CN) /Au = - 0.60 V ; E°O /OH = 0,40 V .
2
2
-
Esercizio 17
Prevedere se le seguenti reazioni di ossido-riduzione avvengono spontaneamente in
condizioni standard:
2

a)
2 Ag + Cu(aq)
2 Ag(aq)
+ Cu
b)
noti E°Cu
2+
/Cu
2
Fe + Cu(aq)
2
Fe(aq)
+ Cu
= 0,34 V; E°Ag /Ag = 0,80 V; E°Fe
+
2+
/Fe
= -0,44 V
E calcola le energie libere molari standard di formazioni (G°f) degli ioni Ag+ e Cu2+.
3.10 Relazione tra ∆E° e Keq
Calcolo del Rapporto Prodotti/Reagenti all'Equilibrio
Benché sia assai importante sapere se una data reazione di ossido-riduzione può
avvenire o meno in condizioni standard, ciò non basta a chi deve condurre la reazione
in laboratorio. Innanzitutto le condizioni standard sono molto particolari da riprodursi
Pagina 24
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
e, inoltre, è altrettanto importante conoscere fino a che punto la reazione può
procedere.
La variazione d'energia libera standard (∆G°reaz) di una reazione è in relazione sia con
la Keq della stessa che con la f.e.m. standard (∆E° pila) della corrispondente ipotetica
pila:
G°reaz = - 2,3 RT log Keq
G°reaz = - nF E°pila
Combinando le due equazioni, si ottiene:
RT
log Keq
nF
e sostituendo per R, F e T i valori in unità di misura congruenti si ha:
0,059
n E°
e
E° =
log Keq
log Keq =
n
0,059
E° = 2,3
dove: n = numero di elettroni scambiati; E°pila = E°red + E°ox = E°
+
red
– E°
-
red
.
Quest'equazione consente il calcolo di Keq 2 di una qualsiasi reazione di ossidoriduzione in base alla conoscenza dei potenziali standard delle coppie redox che
partecipano alla razione.
Quanto più le due coppie redox differiscono nel loro potere ossidante e riducente
(cioè, tanto più elevata è la differenza dei potenziali standard), tanto più il rapporto
prodotti/reagenti all'equilibrio (Keq) è elevato3 e, quindi, tanto più la reazione è
spostata a destra, cioè completa.
Esercizio 18
Calcolare la costante d'equilibrio delle seguenti reazioni di ossido-riduzione noti i
potenziali standard delle varie coppie redox:
2
2
a)
Zn + Cu(aq)
Zn(aq)
+ Cu
b)
2
Sn + Pb(aq)
2
Sn(aq)
+ Pb
c)

Ag + Tl(aq)

Ag(aq)
+ Tl
E°Cu2+/Cu = 0,34 V; E°Zn 2+/Zn = - 0,76 V; E°Sn2+/Sn = - 0,136 V; E°Pb2+/Pb = - 0,126 V;
E°Ag+/Ag = 0,80 V; E°Tl+/Tl = - 0,34 V
2
Occorre sottolineare che Keq non ha dimensioni, mentre Kc è dimensionata. La relazione è Keq = Kc . (M)-n.
Una Keq elevata non significa che la reazione abbia effettivamente luogo ma solo che è possibile dal punto di vista
termodinamico: fattori cinetici potrebbero impedire che la reazione avvenga nella realtà.
3
Pagina 25
BIC
3.11
Equilibrio di ossido-riduzione
AS 2005/2006
Tipi di Semielementi
Esistono semielementi nei quali l'elettrodo partecipa direttamente alla semireazione
che genera il potenziale ed altri in cui l'elettrodo è chimicamente inerte pur
assumendo un definito valore di potenziale.
Di seguito analizziamo i tipi più comuni mettendo in risalto di ciascuno il modo di
schematizzazione simbolica, il relativo equilibrio redox e l'equazione del potenziale
secondo Nernst.
Semielementi di Ia specie (o metallici): sono costituiti da un metallo (Me) a contatto
con una soluzione dei suoi ioni (Men+), generalmente un suo sale solubile.
n+
Me(aq)
+ n eMe
Il potenziale di questi semielementi
concentrazione) degli ioni positivi Men+.
dipende
dall'attività
Esempi:
dalla
0,059
log Zn2+ 
2
0,059
+
log Ag+ 
1
Zn ; EZn2+/Zn = E°Zn2+/Zn +
2+
Zn(aq)
+ 2 e-
+
Semielemento ad argento: Ag(aq)
+ e-
noi
0,059
log Men+ 
n
EMen+/Me = E°Men+/Me +
Semielemento a zinco:
(per
; EAg+/Ag = E°Ag+/Ag
Ag
Semielementi di IIa specie: sono costituiti da un metallo (Me) a contatto con una fase
solida di un suo sale poco solubile (MeX) immersi in una soluzione contenente un sale
solubile con lo stesso anione (Xn-).
nMeX(s) + n eMe + X(aq)
Il potenziale di questi semielementi
concentrazione) degli ioni negativi Xn-.
EMeX/Me = E°MeX/Me +
Esempi:
Semielemento a cloruro d’argento:
Ag/AgCl(s) , Cl-(aq)
Semielemento a calomelano:
Hg/Hg2Cl2 (s) , Cl-(aq)
dipende
dall'attività
(per
0,059
1
log
n
Xn- 
AgCl(s) + e-
Ag + Cl(aq)
EAgCl/Ag = E°AgCl/Ag +
Hg2Cl2 (s) + 2 e-
0,059
1
log
1
Cl- 
2 Hg(l) + 2 Cl(aq)
EHg2Cl2/Hg = E°Hg2Cl2/Hg +
Pagina 26
0,059
1
log
2
2
Cl- 
noi
dalla
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Semielementi a gas: sono costituiti da un metallo inerte (normalmente Pt, Au oppure
grafite) su cui gorgoglia una specie gassosa, entrambi immersi in una soluzione
contenente ioni derivanti da quella specie. In questi semielementi la funzione del
metallo o grafite è quella di favorire l'assorbimento del gas e di condurre la corrente
elettrica.
Esempi:
+
Semielemento ad idrogeno:
2 H3O(aq)
+ 2 eH2 (g) + 2 H2O(l)
Pt, H2 (g)/H3O+(aq)
H3O+ 
0,059
+
log
2
pH2
EH 0+/H = E°H 0+/H
3
Semielemento a ossigeno:
2
3
2
2 H2O(l) + O2 (g) + 4 e-
Pt, O2 (g)/OH -(aq)
2
4 OH-(aq)
pO2
0,059
log
4
4
OH - 
2 Cl(aq)
EO /OH - = E°O /OH - +
2
Semielemento a cloro:
2
Cl2(g) + 2 e-
C(s. graf), Cl2 (g)/Cl -(aq)
ECl /Cl - = E°Cl /Cl - +
2
2
pCl2
0,059
log
2
2
Cl - 
Semielementi redox (o di ossido-riduzione): sono costituiti da un metallo inerte (Pt o
Au) a contatto con una soluzione contenente una coppia redox, cioè stati di
ossidazione diversi di una stessa specie chimica.
Esempi:
3+
2+
Pt/Cr3+(aq), Cr2+(aq)
Cr(aq)
+ eCr(aq)
Cr3+ 
0,059
ECr3+/Cr2+ = E°Cr3+/Cr2+ +
log
1
Cr2+ 
4+
2+
Sn(aq)
+ 2 eSn(aq)
Au/Sn4+(aq), Sn2+(aq)
ESn4+/Sn2+ = E°Sn4+/Sn2+ +
Sn 4+ 
0,059
log  2+ 
2
Sn 
Il potenziale di un semielemento è funzione non solo delle attività delle specie
ossidate e ridotte, ma di tutte le specie che contribuiscono allo specifico equilibrio
redox. La presenza di ioni, quali H3O+ e OH- può influenzare notevolmente il valore del
potenziale e quindi occorre tenerne conto nell'equazione di Nernst:
Pt/MnO4-(aq), Mn2+(aq), H3O+(aq)
+
MnO4- (aq) + 8 H3O(aq)
+ 5 e-
EMnO- ,H O+/Mn2+ = E°MnO- ,H O+/Mn2+
4
3
4
Pagina 27
3
2+
Mn(aq)
+ 12 H2O(l)
MnO4-  H3O+ 
0,059
+
log
5
Mn2+ 
8
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Pt/ClO4-(aq), ClO3-(aq), H3O+(aq)
+
ClO4- (aq) + 2 H3O(aq)
+ 2 e-
ClO3- (aq) + 3 H2O(l)
EClO- ,H O+/ClO- = E°ClO- ,H O+/ClO4
3
3
4
3
3
ClO4-  H3O+ 
0,059
+
log 
2
ClO3- 
2
Semielementi ad amalgama: sono essenzialmente elettrodi di Ia specie in cui il metallo
(Me) invece di essere allo stato puro è disciolto in un altro metallo (di solito Hg) ed è
a contatto con una soluzione dei suoi ioni (Men+).
Esempi:
+
Hg(Na)/Na+(aq)
Na(aq)
+ Hg(l) + eHg(Na)
ENa+/Na(Hg) = E°Na+/Na(Hg) +
Hg(Mg)/Mg2+(aq)
0,059
log Na+ 
1
2+
Mg(aq)
+ Hg(l) + 2 e-
EMg2+/Mg(Hg) = E°Mg2+/Mg(Hg) +
Hg(Mg)
0,059
log Mg2+ 
2
Occorre sottolineare che nell'equazione di Nernst l'argomento del logaritmo, dove
compaiono le attività e le pressioni, è privo di dimensioni in quanto è implicitamente
sottointeso lo stato standard di riferimento di ciascuna specie: per esempio,
0,059
l'espressione generica del potenziale E = E° +
log Men+  equivale a:
n
Men+ 
0,059
E = E° +
log
n
Men+ s tan dard
dove Men+ s tan dard = 1,00 M
Di conseguenza nei calcoli che riguardano i potenziali come argomento del logaritmo si
considera solo il valore numerico calcolato esprimendo le attività in M per le specie in
soluzione e in atm per le specie gassose.
3.12 Aspetti quantitativi delle pile
Una cella galvanica o pila è un dispositivo elettrochimico che trasforma l'energia
associata ad un processo spontaneo (∆G < 0) in energia elettrica (Lel = nF ∆E > 0). In
una cella galvanica di tipo chimico (pila chimica) si sfrutta la variazione d'energia
libera che accompagna un processo chimico spontaneo: il processo elettromotore,
somma dei singoli processi ossidativo e riduttivo che avvengono ai semielementi, è una
Pagina 28
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
reazione chimica spontanea (di ossido-riduzione, di precipitazione, di neutralizzazione,
ecc.).
In una cella galvanica di concentrazione (pila di concentrazione) si sfrutta la
variazione d'energia libera determinata da un processo fisico spontaneo: i singoli
processi che avvengono ai semielementi sono di tipo ossidativo e riduttivo, ma il
processo elettromotore globale è un processo fisico spontaneo (di diluizione o di
espansione).
3.12.1 Pile Chimiche
Qualsiasi reazione chimica spontanea può quindi costituire una sorgente d'energia
elettrica se condotta in modo tale che l'energia chimica del trasferimento degli
elettroni possa essere utilizzata. Come già abbiamo precedentemente illustrato, una
pila chimica è essenzialmente costituita dall'accoppiamento opportuno di due
semielementi. L'energia elettrica prodotta è dovuta alla reazione chimica che in essa
avviene (processo elettromotore).
Per schematizzare una pila si indica con una linea verticale (/) il contatto tra
elettrodo e soluzione, con una doppia linea verticale (//) il contatto tra le soluzioni. I
costituenti presenti su uno stesso elettrodo, o in una stessa soluzione, vengono
separati con una virgola. Lo stato fisico dei costituenti si indica tra parentesi: (aq) per
le soluzioni acquose, (s) per i solidi, (g) per i gas. Occorre inoltre indicare le attività
dei costituenti.
Si voglia schematizzare la pila standard corrispondente alla reazione redox:
Zn + 2 Ag+(aq)  Zn2+(aq) + 2 Ag
presa come esempio all'inizio del capitolo, calcolarne la f.e.m. e quindi la quantità
d'energia chimica che può essere trasformata in energia elettrica.
Schematizzazione
Semielemento di Zinco:
Semielemento di Argento:
Pila chimica Zinco-Argento:
Zn/Zn2+(aq) , 1 M
Ag/Ag+(aq) , 1 M
Zn/Zn2+(aq) , 1 M // Ag/Ag+(aq) , 1 M
Equilibri redox e Potenziali di semielemento
Semielemento di Zinco:
2
Zn(aq)
+ 2 e-

+ eSemielemento di Argento: Ag(aq)
0,059
log Zn2+ 
2
0,059
+
log Ag+ 
1
Zn EZn2+/Zn = E°Zn2+/Zn +
Ag
Pagina 29
EAg+/Ag = E°Ag+/Ag
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Polarità della pila
La polarità della pila si trova calcolando i potenziali di entrambi i semielementi
separatamente ed attribuendo il polo positivo (+) al semielemento a potenziale
maggiore; ovviamente l'altro semielemento costituirà il polo negativo (-).
Generalmente si riscontra che, dati due semielementi 1 e 2, se E°2 > E°1 di circa
0,2-0,3 volt, risulta che E2 > E1 a prescindere dalle concentrazioni delle specie
presenti nelle soluzioni, eccetto nei semielementi per i quali il potenziale E dipende dal
pH (in cui sono cioè presenti ioni H3O+ oppure OH-).
Semielemento di Zinco:
E°Zn 2+/Zn = - 0,76 V : polo negativo (-)
Semielemento di Argento:
E°Ag+/Ag = 0,80 V
: polo positivo (+)
Semireazioni nei semielementi e Processo elettromotore
2+
Polo negativo (-): semireazione di ossidazione
Zn  Zn(aq)
+ 2 ePolo positivo (+):
semireazione di riduzione

Ag(aq)
+ e-  Ag
Il processo elettromotore è rappresentato dal processo chimico (reazione redox):
Zn + 2 Ag+(aq)  Zn2+(aq) + 2 Ag
quando 2 mol di elettroni (2
6,02 1023 e-) fluiscono dal polo negativo (-) al polo
positivo (+) nel circuito esterno, 1 mol di Zn metallico (6,02 1023 atomi di Zn) va in
soluzione come ioni Zn2+ mentre 2 mol di ioni Ag+ (2 6,02 1023 ioni Ag+) si depositano
come Ag metallico.
Forza elettromotrice e Lavoro elettrico
La f.e.m. si calcola facendo la differenza tra il potenziale del polo positivo (+) e il
potenziale del polo negativo (-):
Epila = E +red - E - red

0,059
0,059

 

Epila = EAg+/Ag - EZn2+/Zn =  E°Ag+/Ag +
log Zn2+   =
log Ag+   -  E°Zn2+/Zn +
2
1

 

0,059
0,059

 

=  E°Ag+/Ag +
log 1  -  E°Zn2+/Zn +
log 1  = 0,80 – (-0,76) = 1,56 V
1
2

 

In questo caso abbiamo che Epila = E°pila
Il lavoro elettrico ottenibile dalla pila, per mole di Zn, corrisponde alla diminuzione
d'energia libera (G°reaz) che accompagna il processo elettromotore:
Lel = nF Epila = 2 [mol e-]
9,65 104 [C(mol e-)-1]
1,56 V = 30,1

G°reaz = - Lel = - 30,1
104 J = - 72000 cal
Pagina 30
104 J
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Avevamo visto (cfr. p 10) che la stessa reazione del processo elettromotore fatta
avvenire per diretto mescolamento dei reagenti in un calorimetro sviluppava 87.000
cal (H°reaz = - 87000 cal) d'energia termica non utilizzabile.
Mediante, invece, l'ausilio della pila chimica è possibile convertire una buona parte
dell'energia sviluppata (G°reaz = - 72000 cal) in lavoro elettrico, cioè energia
elettrica.
La parte dell'energia sviluppata, che si manifesta sotto forma di calore di natura
entropica:
T S°reaz = H°reaz - G°reaz = - 87000 – (-72000) = - 15000 cal
non può essere utilizzata per produrre lavoro utile in base al II principio della
termodinamica.
Costante d'equilibrio (Keq)
All'equilibrio la variazione dell'energia libera della reazione del processo
elettromotore è nulla (∆Greaz = 0), di conseguenza è nulla la f.em. della pila (∆Epila = 0)
ed i potenziali dei due semielementi sono uguali ( E-Zn 2+/Zn = E+Ag+/Ag )
In queste condizioni le concentrazioni delle specie presenti sono quelle proprie
dell'equilibrio e risulta G°reaz = - 2,3 RT log Keq
Quindi sostituendo i valori dei potenziali si ottiene :
Keq = 1053
2+
Zn(aq)

n
53
(1-2)
53
-1


Da cui Kc = Keq M = 10 M
= 10 M =
2
+
Ag(aq) 


3.12.2 Pile di concentrazione
Se due soluzioni di ioni Ag+ a diversa concentrazione, l'una 1 M e l'altra 0,01 M,
inizialmente poste in scomparti separati, vengono messe a contatto tra di loro esse
tenderanno a mescolarsi fino a quando le concentrazioni si eguagliano.
Poiché questo processo fisico è spontaneo (∆G < 0) e non presenta effetti termici
apprezzabili, il sistema dispone inizialmente di una quantità d'energia pari al ∆G di
mescolamento delle soluzioni. È possibile sfruttare quest'energia disponibile (∆Gmesc)
e trasformarla in energia elettrica mediante un dispositivo elettrochimico chiamato
pila di concentrazione.
È possibile realizzare una pila di concentrazione facendo eguagliare le concentrazioni
degli ioni Ag+ nelle due soluzioni (quella a concentrazione minore e quella a
concentrazione maggiore) per mezzo di processi ossido-riduttivi nei due distinti
scomparti, ciascuno dei quali costituirà un semielemento.
Pagina 31
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Questi semielementi sono uguali tra di loro come concezione (barretta di Ag metallico
immersa in soluzione di ioni Ag+) ma differiscono per le concentrazioni degli ioni Ag+.
La d.d.p. che si crea tra metallo e soluzione dipenderà solo dalla concentrazione degli
ioni Ag+ presenti, per cui il semielemento con Ag+  = 0,01 M sarà il polo negativo e
quello con Ag+  = 1 M sarà il polo positivo.
Collegando le due barrette di Ag con un conduttore metallico ed i due scomparti
contenenti le due soluzioni con un setto poroso (conduttore elettrolitico) si realizza
un circuito in cui gli elettroni possono fluire dal polo negativo al polo positivo
(originando così corrente elettrica) ed in cui gli ioni possono migrare da un
semielemento all'altro (mantenendo così l'elettroneutralità delle soluzioni).
Pur essendo i singoli processi che avvengono nei semielementi di tipo ossidativo




( Ag  Ag(0,01
M)  e ) e riduttivo ( Ag(1 M)  e  Ag ), il processo elettromotore equivale
sostanzialmente al "trasferimento" di ioni Ag+ dalla soluzione a concentrazione
maggiore (1 M) a quella a concentrazione minore (0,01 M).
Durante il funzionamento della pila, la concentrazione della soluzione più diluita
( Ag+  = 0,1 M) aumenta gradualmente e altrettanto diminuisce la concentrazione
della soluzione più concentrata ( Ag+  = 1 M).
Quando entrambe le soluzioni hanno la stessa concentrazione, la d.d.p. si annulla, il
flusso di elettroni s'interrompe e la pila non è più in grado di fornire energia elettrica.
Pagina 32
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Si voglia schematizzare la pila di concentrazione con semielementi a Ag citata sopra,
calcolarne la f.e.m. e la quantità d'energia chimica trasformabile in lavoro elettrico.
Schematizzazione
Semielemento 1:
Semielemento 2:
Pila di concentrazione:
Ag/Ag+(aq) , 0,1 M
Ag/Ag+(aq) , 1 M
Ag/Ag+(aq) , 0,1 M // Ag/Ag+(aq) , 1 M
Equilibrio redox e Potenziale di semielemento
Semielementi 1 e 2:

Ag(aq)
+ e-
Ag
EAg+/Ag = E°Ag+/Ag +
0,059
log Ag+ 
1
Proprietà della pila
Essendo il potenziale standard E° uguale per entrambi, il potenziale E dipenderà
solamente dalle concentrazioni degli ioni Ag+(aq) nei due semielementi:
Semielemento 1:
Semielemento 2:
Ag+  = 0,1 M
Ag+  = 1 M
In base all'equazione di Nernst risulta che E2 > E1, quindi la polarità della pila sarà:
Semielemento 1: polo negativo (-)
Semielemento 2: polo positivo (+)
Semireazioni nei semielementi e Processo elettromotore


Polo negativo (-): semireazione di ossidazione:
Ag  Ag(aq,
0,1 M)  e
Polo positivo (+): semireazione di riduzione:


Ag(aq,
1 M)  e  Ag
Il processo elettromotore è rappresentato dal processo fisico (mescolamento delle
soluzioni):


Ag(aq,
1 M)  Ag(aq, 0,1 M)
Quando 1 mol di elettroni fluiscono dal polo negativo (-) al polo positivo (+) nel circuito
esterno, la reazione risultante consiste nel trasferimento di 1 mol di ioni Ag+ dalla
soluzione a concentrazione maggiore (1 M) a quella a concentrazione minore (0,1 M).
Forza elettromotrice e Lavoro elettrico
Epila = E
+
red

- E – red = E2 – E1




Pagina 33
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
0,059
0,059

+
+
  -  E°Ag+/Ag +
  =
Epila =  E°Ag+/Ag +
log Ag(0,1M)
log Ag(1M)
1
1

 


Ag(1 M) 
0,059
0,059
1
log    =
=
= 0,059 V
log
1
1
0,1
Ag(0,1 M) 
Il lavoro elettrico ottenibile dalla pila di concentrazione corrisponde alla diminuzione
d'energia libera (∆Gmesc) che accompagna il processo elettromotore:
Lel = nF Epila = 1 [mol e-]
9,65 104 [C(mol e-)-1]

G°mesc = - Lel = - 5.69
0,059 V = 5,69
103 J
103 J = - 1362 cal
Per il trasferimento di 1 mol di ioni Ag+ dalla soluzione a concentrazione maggiore (1
M) a quella a concentrazione minore (0,1 M), la variazione di entalpia (∆Hmesc) è, con
buona approssimazione, uguale al calore sviluppato nella diluizione della soluzione a
concentrazione maggiore diminuito del calore assorbito dalla soluzione a
concentrazione minore.
Poiché queste variazioni di concentrazione delle due soluzioni sono molto piccole, i
calori sviluppati ed assorbiti sono pure molto piccoli e si compensano, quindi ∆H mesc si
può considerare trascurabile:
G°mesc = - T S°mesc
e poiché la pila opera alla temperatura standard di 25°C:
-Gmesc
- 1362 cal
S°mesc =
=
= 4,57 cal K-1
T
298 K
3.13 Potenziale elettrico e pH
Consideriamo la semireazione
Aoss + n e-
la cui costante d'equilibrio è
Keq =
Arid
Arid 
n
Aoss  e  
Il potenziale della copia Aoss/Arid è dato dall'equazione
RT
1
EAoss/Arid =
ln
nF
e- 
Risolvendo la (1) rispetto a
(1)
(2)
1
ed introducendo il valore ottenuto nella (2), si ottiene
 e - 
Pagina 34
BIC
Equilibrio di ossido-riduzione
EAoss/Arid =
A 
RT
RT
ln K +
ln oss
nF
nF
Arid 
AS 2005/2006
(3)
Alle condizioni standard, le concentrazioni della forma ossidata e della forma ridotta
sono uguali a uno, perciò
RT
EAoss/Arid =
ln K + 0 = E°Aoss/Arid
nF
Il potenziale della coppia (semicella) considerata è quindi
A 
RT
(4)
EAoss/Arid = E°Aoss/Arid +
ln oss
nF
Arid 
Consideriamo ora la semicella H+/H2/Pt, la cui reazione è
2 H+ + 2 eH2
Se l'idrogeno è alla pressione di 1 atm, dalla (4) si ottiene
2
EH+/H = E°H+/H
2
2
H+ 
2
RT
RT
RT
+
ln   = 0 +
ln H+  =
ln H+ 
2F
1
2F
F
Siccome i protoni in soluzione acquosa formano ioni idronio, si può scrivere
RT
EH+/H =
ln H3O+ 
2
nF
e a 298 K
EH+/H = 0,059 log H3O+ 
2
Consideriamo ora la pila a concentrazione formata da due semielementi ad idrogeno di
cui uno in condizioni standard ( pH2 = 1 atm e H3O+  = 1 M) e l’altro dove H3O+  < 1 M.
Se applichiamo quanto visto per le celle a concentrazione, troveremo che il
semielemento con H3O+  = 1 M sarà il catodo mentre il semielemento con H3O+  < 1
M sarà l’anodo. Definiamo per semplicità il semielemento con le condizioni standard
come elettrodo di riferimento e l’altro come elettrodo di misura.
Quindi i potenziali degli elettrodi sono:
Ecatodo = 0,059 log 1 = 0
Eanodo = 0,059 log H3O+ 
Il potenziale della cella è
Ecella = 0-0,059 log H3O+ 
Siccome
pH = - log H3O+ 
si ha
pH =
Ecella
0,059
Pagina 35
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Se invece di prendere come riferimento un elettrodo standard di idrogeno si prende
un elettrodo saturo a calomelano, si ottiene
Ecella = -0,2776 - 0,059 log H3O+ 
e quindi
pH =
Ecella  0,2776
0,059
Si sostituisce pure l'idrogeno gassoso dell'elettrodo di misura con un elettrodo di
vetro che si introduce direttamente nella soluzione di cui si vuole misurare il pH. Il
potenziale della cella è misurato da un potenziometro chiamato pHmetro.
Pagina 36
BIC
Equilibrio di ossido-riduzione
4.
Elettrochimica II
4.1
Processi elettrolitici
AS 2005/2006
Come visto in precedenza le reazioni spontanee (∆G < 0) si possono sfruttare per
costruire pile che trasformano direttamente l'energia chimica in energia elettrica. Le
reazioni che invece spontaneamente non potrebbero avvenire (∆G > 0) sono rese
possibili fornendo energia elettrica dall'esterno con trasformazione della stessa in
energia chimica. Questa trasformazione costituisce il fenomeno dell'elettrolisi ed il
dispositivo in cui essa avviene è detto cella elettrolitica; nella pratica si utilizza una
sorgente di corrente elettrica continua per provocare una reazione di ossidoriduzione in una soluzione elettrolitica o in un sale fuso.
Un dispositivo per elettrolisi è costituito da un generatore di corrente continua i cui
terminali sono collegati, per mezzo di fili conduttori, a due elettrodi (anodo e catodo)
immersi in una soluzione elettrolitica (soluto An+ Bn- e solvente H2O) o sale fuso
(An+ Bn-) contenuti in una cella.
Analizziamo cosa avviene quando il circuito è chiuso e vi è passaggio di corrente
d’intensità apprezzabile.
Nel circuito esterno, gli elettroni fluiscono dal polo negativo del generatore al catodo
della cella elettrolitica e dall’anodo di questa al polo positivo del generatore: quindi
all’esterno della cella si ha un continuo flusso di elettroni dall’anodo al catodo.
All’interno della soluzione, gli ioni positivi e gli ioni negativi migrano verso gli elettrodi
di segno opposto, cioè verso il catodo e l’anodo rispettivamente: quindi, all’interno
della cella si ha trasferimento di elettroni dal catodo (che ne è sovraccaricato) agli
ioni positivi o alle molecole neutre della soluzione, mentre contemporaneamente
Pagina 37
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
elettroni vengono trasferiti all’anodo (che ne è deficitario) dagli ioni negativi o dalle
molecole neutre della soluzione.
Questi processi di trasferimento di elettroni che si compiono sulla superficie degli
elettrodi rappresentano il momento di transizione tra il trasporto ionico delle cariche
elettriche all’interno della soluzione ed il trasporto elettronico attraverso il circuito
esterno.
4.2
Semireazioni di scarica agli elettrodi
Le semireazioni che possono avvenire agli elettrodi sono di tipo diverso a seconda
della natura degli elettrodi (inerti o reattivi), delle specie presenti nella soluzione
(ioni positivi e negativi di tipo diverso del soluto e del solvente, oppure molecole
neutre del solvente) e della loro concentrazione nella stessa.
Quando si chiude il circuito, al catodo si ha un accumulo di elettroni e, durante
l’elettrolisi, avviene la semireazione che tende a rimuovere dall’elettrodo l’eccesso di
elettroni, cioè avviene la riduzione degli ioni positivi (An+ o H3O+) o delle molecole
neutre (solvente H2O):
Riduzione catodica:
n+
A(aq)
+ n e-  A

+
2 H3O(aq) + 2 e  H2 (g) + 2 H2O(l)

2 H2O(l) + 2 e  H2 (g) + 2 OH(aq)
All’anodo si ha un difetto di elettroni e, durante l’elettrolisi, avviene la semireazione
che tende a cedere all’elettrodo un ugual numero di elettroni, cioè avviene
l’ossidazione degli ioni negativi (Bn- o OH-) o delle molecole neutre (solvente H2O):
Ossidazione anodica:
nB(aq)
 B + n e
4 OH(aq)  O2 (g) + 2 H2O(l) + 4 e

+
6 H2O(l)  O2 (g) + 4 H3O(aq) + 4 e
Se l’anodo, anziché da un elettrodo inerte (quali Pt o Cgrafite che sono inossidabili), è
costituito da un elettrodo reattivo può avvenire l’ossidazione del metallo che
costituisce l’elettrodo stesso:
n+
Me  Me(aq)
+ n eLa reazione globale che avviene nella cella elettrolitica è la somma delle semireazioni
che avvengono al catodo e all’anodo.
Pagina 38
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Diversamente dalle celle galvaniche, nelle celle elettrolitiche le semireazioni di
riduzione e di ossidazione avvengono rispettivamente al catodo (negativo) e all’anodo
(positivo) in quanto collegati l’uno (catodo) con il polo negativo e l’altro (anodo) con il
polo positivo del generatore.
4.3
Ordine di scarica delle specie chimiche agli elettrodi
Tutte le specie ioniche presenti, sia positive che negative, provvedono, con la
migrazione verso gli elettrodi di segno opposto, al trasporto della corrente elettrica,
ma solo alcune di esse si scaricano agli elettrodi: si riducono e si ossidano
preferibilmente le specie che richiedono il minor lavoro elettrico (Lel) e quindi la minor
d.d.p. applicata (∆E). In pratica su ciascun elettrodo avviene la semireazione
energeticamente meno difficile, ovvero quella che richiede minor energia e
precisamente:
 all’anodo (+) si ossida la specie più riducente, cioè con potenziale minore;
 al catodo (-) si riduce la specie più ossidante, cioè con potenziale maggiore.
Pertanto il confronto tra i valori dei potenziali E° nelle condizioni standard oppure tra
i potenziali E nelle condizioni specificate (calcolati con l’equazione di Nernst) delle
varie specie chimiche presenti consente di stabilire l’ordine discarica.
4.4
Potenziale di decomposizione e forza controelettromotrice
Quando le specie chimiche presenti si scaricano, gli elettrodi si polarizzano
trasformandosi così in semielementi di una pila chimica cortocircuitata che genera una
forza elettromotrice contraria (f.c.e.m.) che si oppone al passaggio di corrente
imposto dall'esterno. Perché il processo di elettrolisi avvenga in modo continuo
occorre che la d.d.p. applicata superi il valore della massima f.c.e.m. generata dalla pila
indotta.
La differenza Ean - Ecat, che è il valore della massima f.c.e.m., rappresenta perciò la
minima d.d.p. da applicare affinché avvenga l'elettrolisi: tale valore è noto come
potenziale di decomposizione Ed.4
Quindi, conoscendo tutte le specie chimiche presenti e le possibili semireazioni a cui
esse potrebbero dar luogo agli elettrodi, consultando i valori di E° tabulati e
calcolando i valori di E mediante l'equazione di Nernst, è possibile prevedere
Ean e Ecat rappresentano i potenziali di riduzione associati alle semireazioni elettrodiche che avvengono
all'anodo (ossidazione) e al catodo (riduzione) rispettivamente.
4
Pagina 39
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
effettivamente quali specie si ossideranno e si ridurranno e quale sarà la d.d.p. minima
da applicare.
4.5
Potenziale pratico di elettrolisi
Il valore Ed = (Ean - Ecat) calcolato perché avvenga l'elettrolisi si riferisce a condizioni
d'equilibrio termodinamico ed è valido per un processo elettrochimico che viene
condotto reversibilmente, quindi rappresenta solo il valore teorico della minima d.d.p
che deve essere applicata ad una cella elettrolitica per provocare una reazione non
spontanea.
Nella pratica la d.d.p da applicare è maggiore del potenziale di decomposizione E d: più
le condizioni di reazione si allontanano da quelle di reversibilità termodinamica tanto
maggiore è la d.d.p. che si deve applicare rispetto al valore minimo Ed calcolato.
La differenza tra il valore teorico Ed e quello pratico Epr è dovuta sia a fenomeni di
sovratensione che di caduta ohmica:
Epr = Ed +  + I  R
ovvero:
dove:
Epr
=
Epr = Ean - Ecat  +  an  cat  + I  R
potenziale pratico d'elettrolisi;
Ed
=

=
potenziale di decomposizione dovuto alla polarizzazione chimica degli
elettrodi (f.c.e.m. della pila indotta);
sovratensione dovuta a fattori cinetici (difficoltà degli ioni a scaricarsi e
=
diversa velocità di migrazione);
caduta ohmica dovuta alla resistenza propria della soluzione elettrolitica
I R
Solamente
il
potenziale
di
decomposizione
Ed
può
essere
calcolato
termodinamicamente, mentre la sovratensione  e la cauta ohmica I  R dipendono da
diversi fattori quali la temperatura, la concentrazione degli elettroliti, la densità di
corrente, la natura e la superficie degli elettrodi.
Esercizio 19
Al catodo di una cella elettrolitica sono presenti in soluzione acquosa, a
concentrazione unitaria, i seguenti ioni: Cu2+, Ag+ e Zn2+.
Noti i potenziali standard E°Cu /Cu = 0,34 V ; E°Ag /Ag = 0,80 V ; E°Zn /Zn = -0,76 V e
+
2+
2+
trascurando il solvente H2O, prevedere quale specie si scarica per prima.
Pagina 40
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esercizio 20
All'anodo di una cella elettrolitica sono presenti in soluzione acquosa, a
concentrazione unitaria, i seguenti ioni: F -, Cl - e I -.
Noti i potenziali standard E°F /F = 2,85 V ; E°Cl /Cl = 1,36 V ; E°I /I = 0,54 V e
2
-
2
-
2
-
trascurando il solvente H2O, prevedere quale specie si scarica per prima.
Esercizio 21
Calcolare la f.c.e.m. della pila indotta che si crea in una cella elettrolitica,
sottoponendo a elettrolisi una soluzione acquosa 1,0 M di CoCl2, con elettrodi inerti di
grafite. E°Cl /Cl = 1,36 V ; E°Co /Co = -0,28 V
2
-
2
Esercizio 22
Una cella elettrolitica contiene le seguenti specie chimiche in soluzione acquosa a
concentrazione unitaria: Fe2+, Cu2+, Br - e Cl -.
Trascurando il solvente H2O e in base ai valori dei potenziali standard E°Cl /Cl =1,36 V;
2
-
E°Br /Br- = 1,06 V; E°Cu 2/Cu = 0,34 V; E°Fe 2/Fe = -0,44 V descrivere quale processo avviene
2
e calcolare il lavoro minimo necessario perché si compia l'elettrolisi.
4.6
Aspetti quantitativi dell’elettrolisi – leggi di Faraday
Le leggi di Faraday consentono di ricavare le relazioni che interoccono tra la quantità
di elettricità che attraversa una soluzione elettrolitica o sale fuso e le quantità delle
specie chimiche consumate o prodotte agli elettrodi di una cella. Esse sono facilmente
deducibili qualora si ricordi che:
-
-
la quantità di carica elettrica trasportata da una mole di elettroni è il Faraday:
1 mol e- = 1 Faraday (F) = 96.500 Coulomb ©
la quantità di carica elettrica Q che attraversa una cella dipende dall'intensità
della corrente I e dal tempo t:
Q (C) = I (A) . t (s)
un equivalente è la quantità in grammi di specie chimica ionica o neutra messa in
gioco da 1 mole di elettroni, cioè da 1 Faraday.
Per esempio, nell'elettrolisi di una soluzione acquosa di CuCl2, le semireazioni che
avvengono agli elettrodi sono:
anodo (+):
2 Cl(aq)
 Cl2 (g) + 2 e-
catodo (-):
2+
Cu(aq)
+ 2 e-  Cu(s)
Pagina 41
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Considerando le stesse semirazioni basate sul trasferimento di 1 mole di elettroni:
anodo (+):
Cl(aq)

catodo (-):
1 2+
Cu(aq)
2
1
Cl2 (g) + e2
1
+ e- 
Cu(s)
2
si deduce che, al passaggio di 1 Faraday;
si riduce 1/2 mol ioni Cu2+ a 1/2 mol Cu metallico
si ossida 1 mol Cl- a 1/2 mol Cl2 gassoso
Quindi, le quantità pari a 1/2 mol ioni Cu2+, 1/2 mol atomi Cu, 1 mol ioni Cl- e 1/2 mol
molecole Cl2 sono tutte equivalenti tra di loro e rappresentative di 1 equivalente di ioni
Cu2+(aq), di atomi Cu, di ioni Cl-(aq) e di molecole Cl2 (g).
Di conseguenza la massa equivalente (Meq) e il volume equivalente (Veq) sono ricavabili
dalla massa molare (Mm) e dal volume molare (Vm) tenendo conto del numero di moli di
elettroni (n) messi in gioco per mole di specie chimica, ovvero del numero di
equivalenti (n) per mole, secondo le relazioni:
Meq (g eq-1 ) =
Mm (g mol-1 )
n (eq mol-1 )
;
Veq (L eq-1 ) =
Vm (L mol-1 )
a c. n.
n (eq mol-1 )
Le leggi di Faraday riassumono le relazioni viste:
I LEGGE - La quantità di specie chimica ridotta al catodo o ossidata all'anodo è
proporzionale alla quantità di carica elettrica Q che ha attraversato la cella
elettrolitica:
Meq
m=
Q
F
dove:
m
=
quantità (g) di specie chimica;
Meq =
massa equivalente (g eq-1) di specie chimica;
F
=
costante di Faraday (C eq-1);
Q
=
quantità (C) di carica elettrica
Dalle relazioni Q = I t e Meq =
m (g) =
Mm
si ottiene la relazione da utilizzare per i calcoli:
n
Mm (g mol-1 ) I (C s-1 ) t (s)
n (eq mol-1 ) F (C eq-1 )
Pagina 42
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Quando la specie chimica ridotta al catodo o ossidata all'anodo è gassosa, la sua
quantità può essere calcolata anche in unità di volume facendo riferimento alle
condizioni normali per lo stato gassoso:
V(c.n.) =
dove:
V
=
Veq
=
Veq (c.n.)
F
Q
Volume (L) di specie chimica;
Volume equivalente (L eq-1) di specie chimica;
La relazione da utilizzare per i calcoli è:
V(c.n.)
Vm (L mol-1 ) I (C s-1 ) t (s)
(L) =
n (eq mol-1 ) F (C eq-1 )
II LEGGE - Per una stessa quantità di carica elettrica Q che passa attraverso più
celle elettrolitiche disposte in serie, le quantità delle diverse specie chimiche che si
ossidano o si riducono agli elettrodi sono proporzionali alle loro masse equivalenti:
Q=
m F
m1 F
m F
= 2
= 3
= ...
Meq 1
Meq 2
Meq 3
Nel caso in cui risulti Q = F = 96.500 C, le quantità di specie chimiche (m) che si
ossidano o si riducono sono esattamente le masse equivalenti (Meq), cioè un equivalente
di ciascuna specie.
Esercizio 23
Calcolare la massa equivalente Meq dell'Alluminio e dell'Ossigeno nell'elettrolisi di
Al2O3 fuso, ammettendo le seguenti semireazioni agli elettrodi:
catodo (-):
2 Al3+ + 6 e-  2 Al(l)
anodo (+):
3 O2- 
3
O2 (g) + 6 e2
Esercizio 24
Una corrente di 3,50 A viene fatta passare per 3 min e 30 s in una cella elettrolitica
contenente AuCl3.
Calcolare la quantità in grammi di Au che si deposita al catodo della cella.
Pagina 43
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esercizio 25
Calcolare quanti litri di O2 gassoso a c.n. si sviluppano all'anodo di una cella
elettrolitica contenente una soluzione di Ag2SO4 attraversata da una quantità di
corrente tale da depositare contemporaneamente al catodo 3,8 g di Ag.
Le semireazioni agli elettrodi sono:
catodo (-):
anodo (+):
4.7
2 Ag+ + e-  Ag
6 H2O(l)  O2 (g) + 4 H3O+(aq) + 4 e-
Pile chimiche di interesse pratico
Le pile chimiche trattate non sono pile costruite allo scopo di generare corrente, ma
piuttosto per determinare sperimentalmente, mediante misure di f.e.m., molti dati
termodinamici difficilmente ottenibili in altro modo riguardanti i metalli, le soluzioni e
le reazioni di ossido-riduzione: tali pile rappresentano perciò validissimi mezzi di
ricerca.
In questo paragrafo vengono descritte le pile che più frequentemente sono usate nella
pratica come generatori di corrente.
Le pile chimiche d'interesse ed utilizzo pratico vengono di solito classificate in due
categorie:
 pile chimiche primarie (o irreversibili) che una volta sfruttate come sorgenti
d'energia elettrica non possono essere riportate allo stato originario per le
alterazioni irreversibili determinate dai processi di scarica: le più note sono le pile
a secco e quelle ad elettrolita solido; la loro durata nel tempo dipende dalla quantità
iniziale dei reagenti;
Pila Leclanché
Pila Ruben-Mallory
Pagina 44
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
 pile chimiche secondarie (o reversibili) che invece possono essere ricaricate
mediante una sorgente di corrente continua esterna; le più note sono gli
accumulatori.
Accumulatore al Piombo
Esiste un'altra categoria di pile, dette a combustibile, nelle quali il processo
elettromotore è una reazione di combustione in cui il combustibile (H 2, CH4, carbone,
gas naturale, gas liquido, gasolio, olio combustibile) ed il comburente (O 2) vengono
alimentati di continuo dall'esterno ed i prodotti della reazione vengono continuamente
asportati; esse realizzano rendimenti elevatissimi e sono in grado di produrre energia
elettrica fintanto che il combustibile e l'ossigeno sono disponibili.
Cella combustibile ad idrogeno
Qualsiasi pila che coinvolge liquidi come elettroliti è difficile, nella pratica, da usarsi
in condizioni di movimento. Per questo scopo sono molto utili le pile a secco: la
soluzione acquosa dell'elettrolita è adsorbita su materiale poroso inerte oppure
gelificata con amido e pertanto essa non può scorrere liberamente all'interno della
pila. Un inconveniente di queste pile è che non sopportano le basse e le alte
temperature in quanto l'elettrolita acquoso può gelare od evaporare con perdita
evidente di conducibilità ionica, ma vengono normalmente utilizzate come sorgenti
Pagina 45
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
d'energia elettrica portatile (lampade tascabili, radioline, apparecchi fotografici,
elettrodomestici ed altri strumenti portatili).
Le pile ad elettrolita solido possono invece funzionare in un intervallo ampio di
temperature e durare molto più a lungo, e sono basate sul fatto riconosciuto che in
certi solidi cristallini la mobilità degli ioni è sufficiente per dar luogo a conduzione.
Sebbene le pile reversibili siano molte (es.: pila Daniell, Weston, ...) non tutte possono
trovare interesse pratico come accumulatori, ma solo quella in cui i processi di scarica
e ricarica avvengono senza particolari difficoltà. il loro campo d'applicazione è molto
vasto in quanto vengono usate per l'avviamento dei motori a scoppio e diesel, per
l'illuminazione delle carrozze ferroviarie, per l'alimentazione di strumenti scientifici,
ed in genere come fonti di riserva e d'emergenza d'energia elettrica.
Esercizio 26
La pila a secco tipo Leclanchè può essere così schematizzata:
Zn / NH4Cl(aq) // MnO2 (s), C(s, grafite)
Descrivere il processo elettromotore e calcolare la quantità di Zn metallico consumato
quando la pila ha erogato 35,0 ampere-ora (A h-1).
Esercizio 27
La pila a mercurio, tipo Ruben-Mallory, è una pila a secco molto utilizzata per micro
apparecchiature e può essere così schematizzata:
Zn / KOH(aq) // HgO (s), C(s, grafite)
Descrivere il processo elettromotore e calcolare la f.e.m. in condizioni standard.
Esercizio 28
Un tipo di pila a elettrolita solido è quella Argento-Iodio che può essere
schematizzata nel seguente modo:
Ag / AgI(s) // I2 (s), C(s, grafite)
Descrivere il processo elettromotore e calcolare la f.e.m. in condizioni standard sia
dai dati termodinamici (∆G°reaz = -31,7 kcal) che da quelli di potenziale standard
( E°I /I = 0,535 V ; E°AgI /Ag = -0,151 V)
2
-
Esercizio 29
Un combustibile convenzionale che potrebbe essere utilizzato nelle pile è il metano
CH4. Una pila combustibile di questo tipo può essere così schematizzata:
C(s, grafite), CH4 (g) / KOH(aq) // O2 (s), C(s, grafite)
Descrivere il processo elettromotore dlela pila, calcolare la f.e.m. standard e il
rendimento teorico che si potrebbe ottenere dai seguenti dati termodinamici
(∆G°reaz = -817 kJ e ∆H°reaz = -889,5 kJ)
Pagina 46
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esercizio 30
Calcolare la quantità di elettricità fornita da un accumulatore al piombo in fase di
scarica quando 23,0 g di Pb sono stati ossidati.
Calcolare inoltre la quantità di PbSO4 che si è formata su entrambi gli elettrodi e per
quanto tempo l'accumulatore deve essere ricaricato mediante una corrente di 10,0 A
per riportarlo nelle condizioni originarie.
La reazione che avviene nell'accumulatore in fase di scarica è la seguente:
Pb + PbO2 (s) + 2 H2SO4 (aq)  2 PbSO4 (s) + 2 H2O(l)
Altri Problemi
Esercizio 31
Qual è il valore del potenziale della seguente cella
Ni / Ni2+ (0,01M) // Cl- (0,2 M) / Cl2 (1 atm)
Qual è il valore del ∆G della cella?
Esercizio 32
Calcolare la F.e.m. della pila costituita ai seguenti semielementi galvanici:
Fe / FeSO4 (0,2M) // Pb / Pb(NO3)2 (0,01 M)
Esercizio 33
Calcolare i potenziale di un elettrodo di ferro immerso in una soluzione acquosa satura
di idrossido ferroso (FeII) a un pH = 9.
Esercizio 34
Calcolare la forza elettromotrice della pila costituita dai semielementi
Ni2+ (10-3M) / Ni // Ag+ (5.10-2M) / Ag
Indicare se la reazione avviene spontaneamente e calcolare la costante di equilibrio.
Esercizio 35
Calcolare la quantità di nitrato (AgNO3) decomposta elettroliticamente dal passaggio
di una corrente di 0,5 ampère per 200 minuti.
Esercizio 36
La stessa quantità di elettricità che viene liberata da 2,158 g di argento viene fatta
passare attraverso una soluzione di un sale di oro, e si depositano 1,314 g di oro.
Calcolare la massa equivalente dell'oro e il Numero di Ossidazione dell'oro in questo
sale.
Pagina 47
BIC
Equilibrio di ossido-riduzione
AS 2005/2006
Esercizio 37
Quanto tempo occorre per depositare 100 g di Al, da una cella elettrolitica che
contiene Al2O3, e attraversata da una corrente di intensità pari a 125A.
Pagina 48