+ p

Semiconduttori.
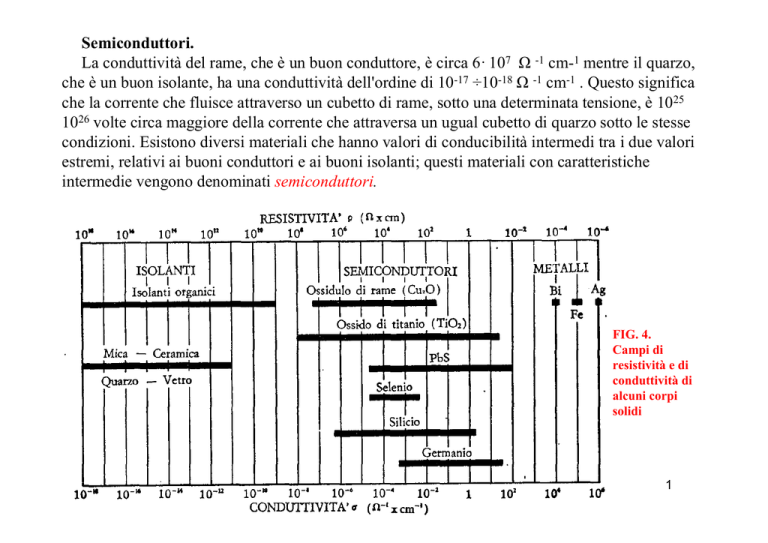
La conduttività del rame, che è un buon conduttore, è circa 6· 107 Ω -1 cm-1 mentre il quarzo,
che è un buon isolante, ha una conduttività dell'ordine di 10-17 ÷10-18 Ω -1 cm-1 . Questo significa
che la corrente che fluisce attraverso un cubetto di rame, sotto una determinata tensione, è 1025
1026 volte circa maggiore della corrente che attraversa un ugual cubetto di quarzo sotto le stesse
condizioni. Esistono diversi materiali che hanno valori di conducibilità intermedi tra i due valori
estremi, relativi ai buoni conduttori e ai buoni isolanti; questi materiali con caratteristiche
intermedie vengono denominati semiconduttori.
FIG. 4.
Campi di
resistività e di
conduttività di
alcuni corpi
solidi
1
Tra di essi si ricorda l'ossidulo di rame Cu20, l'ossido di titanio Ti02, il solfuro di piombo (galena)
PbS, l'arseniuro di gallio GaAs, l'antimoniuro di gallio GaSb, il selenio, il germanio e silicio. In
fig. 4 sono riportati i campi di resistività ρ e di conduttività σ di alcuni conduttori, isolanti e
semiconduttori.
Il numero delle orbite e la distanza di ciascuna di esse dal nucleo sono ben definiti e quindi ogni
atomo possiede livelli di energia ben determinati. I valori intermedi a questi livelli sono detti
livelli di energia interdetti, il che vuol dire che gli elettroni di quell'atomo non possono
raggiungerli, cioè non possono avere i livelli di energia interdetti.
FIG. 4.
Campi di
resistività e di
conduttività di
alcuni corpi
solidi
2
I solidi, che sono formati da un grandissimo numero di atomi, possiedono degli insiemi di livelli
energetici, detti anche bande di energia. Si ha la banda di valenza, alla quale appartengono tutti
gli elettroni presenti nell'orbita più esterna degli atomi e la banda di conduzione, alla quale
appartengono tutti gli elettroni in possesso di un'energia che permette loro di sfuggire
all'attrazione del nucleo, diventando così elettroni liberi. Tra le bande ammesse esiste uno spazio
vuoto (gap) detto anche banda di energia proibita nel senso che in essa non possono esserci
elettroni. In fig. 5 è riportata qualitativamente la situazione nei tre casi di isolante,
seminconduttore e conduttore.
FIG. 5. - Ripartizione delle bande di energia nei materiali supposti chimicamente puri
e a 0°K: (a) isolante: (b) semiconduttore: (c) conduttore.
3
In (a) è rappresentato il caso di un isolante perfetto, cioè di un cristallo chimicamente puro e
senza imperfezioni strutturali alla temperatura di 0 °K. La banda di valenza è completamente
piena, mentre quella di conduzione è completamente vuota; la banda proibita, che le separa, ha
una larghezza di molti elettron-volt. Gli elettroni di valenza non sono in grado di saltare
l'ostacolo della banda proibita e di trasferirsi nella banda di conduzione, che è, come già detto,
vuota. Gli elettroni in questo cristallo sono legati saldamente al reticolo e sotto l'azione di un
normale campo elettrico non danno luogo ad alcuna corrente elettronica.
FIG. 5. - Ripartizione delle bande di energia nei materiali supposti chimicamente puri
e a 0°K: (a) isolante: (b) semiconduttore: (c) conduttore.
4
In (b) sono rappresentate le bande di energia in un semiconduttore come il silicio e il germanio,
nel caso di cristalli puri e alla temperatura di 0 °K; la banda di valenza è completamente piena di
elettroni e dista solo 0,72 eV (*) per il Ge e 1,12 eV per il Si dalla banda di conduzione. In questo
caso è relativamente facile pervenire a condizioni di conducibilità. Infatti già a temperatura
ambiente alcuni elettroni, a causa dell'energia termica che ricevono dall'esterno, riescono a
portarsi nella banda di conduzione.
(*) Un elettronvolt (simbolo eV) è l'energia acquistata da un elettrone libero quando passa
attraverso una differenza di potenziale elettrico di 1 volt nel vuoto. 1 eV = 1,602 × 10-19 J.
FIG. 5. - Ripartizione delle bande di energia nei materiali supposti chimicamente puri
e a 0°K: (a) isolante: (b) semiconduttore: (c) conduttore.
5
In (c) sono rappresentate le bande di energia nel caso di un metallo; una parte della banda di
valenza si sovrappone con quella di conduzione. In questo caso gli elettroni non devono
attraversare alcuna banda proibita; la conduttività, al contrario di quanto accade per i
semiconduttori, aumenta al diminuire della temperatura.
FIG. 5. - Ripartizione delle bande di energia nei materiali supposti chimicamente puri
e a 0°K: (a) isolante: (b) semiconduttore: (c) conduttore.
6
Germanio e silicio.
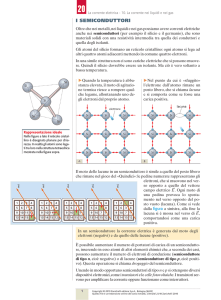
Il germanio e il silicio sono i due semiconduttori più importanti usati nella fabbricazione dei
dispositivi elettronici a stato solido. La struttura cristallina di questi materiali consiste in una
ripetizione regolare, nelle tre direzioni dello spazio, di una cella a forma di tetraedro regolare con
un atomo per ciascun vertice.
In fig. 6 è indicato il reticolo cristallino del germanio o del silicio in cui ciascuna sfera
rappresenta un atomo e i bastoncini che congiungono gli atomi e sorreggono la struttura
rappresentano i legami covalenti fra gli atomi stessi. La dimensione a vale 5,4 Å per il Si e 5,7 Å
per il Ge. (1 Å = 10-10 m)
6. - Struttura cristallina del germanio e del silicio.
7
Nella sua struttura atomica il silicio possiede 14 elettroni, mentre il germanio ne possiede 32;
entrambi sono tetravalenti, cioè presentano solo 4 elettroni nell'orbita più esterna. La fig. 7
mostra la struttura in una rappresentazione semplificata in due dimensioni. I collegamenti a
tratteggio fra i vari atomi rappresentano i legami covalenti, mentre i cerchi in grigio
rappresentano gli atomi di germanio con l'esclusione dei 4 elettroni di valenza; ciò che resta di
ciascun atomo di germanio ha quindi una carica positiva pari a + 4 e, dove e è la carica
dell'elettrone.
FIG. 7. - Rappresentazione simbolica
in due dimensioni della struttura cristallina del Ge.
FIG. 8. - Cristallo di Ge con un legame
covalente rotto.
8
A temperature estremamente basse (intorno a 0°K) ci si avvicina alla struttura ideale di fig. 7 e
il cristallo si comporta come un isolante poiché non vi sono portatori di carica liberi e quindi
disponibili per la conduzione di corrente. Alla temperatura ambiente (300°K), tuttavia, alcuni
legami covalenti, a causa dell'agitazione termica, vengono rotti ed è possibile avere conduzione
attraverso il cristallo. La fig. 8 illustra la situazione; in essa si è supposto un solo legame rotto.
La rottura del legame richiede una certa energia pari a circa 1,1 eV per il silicio e a circa 0,72
eV per il germanio, a temperatura ambiente. Alla rottura di un legame covalente si forma nel
cristallo un elettrone libero ed una carica positiva, detta lacuna, nel posto occupato
dall'elettrone prima della rottura.
FIG. 7. - Rappresentazione simbolica
in due dimensioni della struttura
cristallina del Ge.
FIG. 8. - Cristallo di Ge con un
legame covalente rotto.
La lacuna
costituisce un
portatore di
carica
analogamente
all'elettrone
libero ed
entrambi
contribuiscono
alla conduzione
elettrica
attraverso il
cristallo.
9
Il meccanismo mediante il quale una lacuna partecipa alla conduzione di corrente può essere
spiegato qualitativamente come segue: la lacuna formatasi in seguito alla rottura di un legame
covalente, può essere riempita da un elettrone di valenza di un atomo vicino, dal cui legame è in
grado di svincolarsi con relativa facilità. Questo elettrone lascia nel posto occupato
precedentemente una lacuna, che effettivamente viene a muoversi in direzione opposta a quella
dell'elettrone di valenza; quest'ultimo si rende momentaneamente libero. La lacuna, nella sua
nuova posizione, può ora essere riempita da un altro elettrone di valenza proveniente da un altro
atomo e corrispondentemente essa si muoverà di un altro passo in direzione opposta al moto
dell'elettrone.
Nei semiconduttori si hanno quindi due tipi di portatori: gli elettroni e le lacune; quest'ultime
equivalgono ai fini della conduzione elettrica a delle effettive cariche positive libere, di valore
uguale a quella dell'elettrone ( + e). In un semiconduttore esente da qualsiasi impurezza, detto
anche semiconduttore intrinseco, il numero di lacune presenti è uguale al numero di elettroni
liberi. L'agitazione termica produce in continuazione nuove coppie elettrone-lacuna, mentre altre
coppie spariscono per ricombinazione.
In condizioni di equilibrio, il ritmo di produzione delle coppie è uguale al ritmo di
ricombinazione delle coppie stesse.
10
Resistività intrinseca dei semiconduttori.
La conducibilità elettrica nei semiconduttori è dovuta al contributo degli elettroni liberi e delle
lacune. Applicando un campo elettrico E al semiconduttore, queste particelle si muovono in
direzioni contrarie, ma avendo cariche di segno opposto, la corrente dovuta a ciascun tipo di
particella è nella stessa direzione. La densita di corrente J è data da:
(10)
in cui:
e = carica dell'elettrone,
n = concentrazione degli elettroni liberi (numero di elettroni liberi/m3),
p = concentrazione delle lacune (numero di lacune/m3),
µn e µp, = mobilità, rispettivamente, degli elettroni e delle lacune,
σ = conduttività del materiale.
La conduttivith ha perciò l'espressione:
Per un semiconduttore intrinseco è n = p = ni dove ni è la concentrazione intrinseca; l'inverso di
σ è la resistività intrinseca.
Nel germanio puro, a temperatura ambiente, vi è circa una coppia elettrone-lacuna su 2· 1019
atomi di germanio. L'aumento della temperatura è quindi dell'agitazione termica comporta un
aumento del numero di coppie elettrone-lacuna: come conseguenza cresce la conducibilità del
11
semiconduttore intrinseco.
La concentrazione intrinseca dei portatori è legata alla temperatura dalla relazione:
(11)
La resistività intrinseca a temperatura ambiente (circa 27 °C) è di 45 Ω x cm per il germanio e di
230 kΩ x cm per il silicio.
12
Semiconduttori drogati.
Aggiungendo al germanio (o al silicio) puro una piccola quantità d'impurezza pentavalente,
alcuni atomi di germanio nel reticolo cristallino vengono sostituiti dagli atomi d'impurezza (fig.
9). Quattro dei cinque elettroni dell'atomo pentavalente formano i legami covalenti con i quattro
atomi circostanti di germanio, mentre il quinto elettrone è libero e quindi disponibile come
portatore di corrente. Infatti l'energia richiesta per rendere libero questo quinto elettrone è
dell'ordine di appena 0,01 eV per il Ge e di 0,05 eV per il Si.
Il processo mediante il quale si aggiungono impurezze ad un semiconduttore puro è
conosciuto come drogaggio (doping) del semiconduttore.
FIG. 9. - Struttura cristallina con un
atomo di germanio sostituito da un
atomo di impurezza pentavalente (antimonio).
FIG. 10. - Struttura cristallina con un atomo di germanio
sostituito da un atomo di impurezza trivalente (Indio).
13
L'arsenico, il fosforo e l'antimonio sono le impurezze pentavalenti più comunemente usate;
esse vengono denominate impurezze donatrici in quanto forniscono al semiconduttore elettroni
liberi. L'atomo pentavalente donatore, dopo aver ceduto al cristallo l'elettrone libero, rimane
immobilizzato nel reticolo cristallino come ione positivo e non partecipa alla conduzione
elettrica.
Il drogaggio di un semiconduttore con impurezze donatrici fa aumentare in esso il numero
degli elettroni liberi; diminuisce invece numero delle lacune al di sotto del valore che si ha nel
semiconduttore intrinseco. Infatti la presenza nel cristallo drogato, di un maggior numero di
elettroni fa aumentare il ritmo di ricombinazione degli elettroni con le lacune. La conducibilità
del semiconduttore drogato è denominata conducibilità estrinseca ed il suo inverso resistività
estrinseca. Con impurezze pentavalenti (i cui atomi hanno cioè cinque elettroni nell'orbita piü
estema), la conducibilità è dovuta essenzialmente agli elettroni ed il semiconduttore si dice di
tipo N.
Aggiungendo al semiconduttore intrinseco un'impurezza
trivalente (elemento con tre soli elettroni nell'orbita più
esterna), quali il boro, l'indio, il gallio e l'alluminio, soltanto
tre dei quattro legami covalenti possono essere formati con i
quattro atomi di germanio (o di Si) circostanti ed il vuoto che
rimane nel quarto legame costituisce una lacuna;
la fig. 10 illustra questo stato di cose.
FIG. 10. - Struttura crlstallina con un atomo di germanio
sostituito da un atomo di impurezza trivalente (Indio).
14
Poiché le impurezze trivalenti forniscono al cristallo cariche positive (lacune) disponibili come
portatori, esse vengono chiamate impurezze accettrici, in quanto, creando lacune, possono
accettare elettroni di valenza dagli atomi circostanti. L'atomo accettore, dopo aver catturato un
elettrone, rimane immobilizzato nel reticolo cristallino come ione negativo e non partecipa alla
conduzione elettrica attraverso cristallo. Nel semiconduttore drogato con impurezze trivalenti,
aumenta il numero di lacune presenti, mentre quello degli elettroni liberi diminuisce al di sotto
del valore che si ha nel semiconduttore intrinseco, dato che il maggior numero di lacune fa
aumentare il ritmo di ricombinazione. La conducibilità del semiconduttore drogato con
impurezze trivalenti è dovuta essenzialmente alle lacune ed esso si dice di tipo P. Minime tracce
di impurezze alterano notevolmente la conducibilità del semiconduttore; ad esempio l'aggiunta di
un atomo donatore per ogni 10 atomi di germanio, fa aumentare la conducibilità, a 30°C, di un
fattore pari a 12. Mentre donatori (drogaggio di tipo N) ed accettori (drogaggio di tipo P) sono
fissi, gli elettroni e le lacune sono dotate, come già detto, di notevole mobilità e tendono a
diffondersi spontaneamente tutto il materiale. Le lacune e gli elettroni dovuti rispettivamente al
drogaggio di tipo P e a quello di tipo N, si dicono anche portatori di maggioranza, che con i
portatori di minoranza, di origine termica, costituiscono le cariche mobili, in grado di conferire
ai semiconduttori una discreta conducibilità. Si tenga infine ben presente che nei semiconduttori
sia di tipo P che di tipo N, il materiale rimane elettricamente neutro in quanto la somma
algebrica delle cariche positive e negative è sempre nulla.
15
Formazione di una giunzione P-N.
Consideriamo due pezzi di semiconduttore di germanio, uno drogato di tipo P e uno drogato di
tipo N; portandoli a contatto lungo una superficie si ottiene una giunzione. In effetti la
formazione di una giunzione implica processi tecnologici abbastanza complessi, con i quali si
deve mantenere attraverso la giunzione la continuità della struttura cristallina (reticolo) del
materiale semiconduttore usato.
I due pezzi di semiconduttore si presentano inizialmente neutri; infatti nel germanio di tipo P
ci sono tante lacune quanti sono gli atomi accettori e ugualmente nel germanio di tipo N ci sono
tanti elettroni liberi quanti sono gli atomi donatori, non tenendo conto delle coppie elettronelacuna di origine termica. La situazione è illustrata in fig. 11, dove sono rappresentate
schematicamente le cariche fisse (ioni) con un cerchietto recante all'interno un + (donatori) o un
- (accettori), mentre le cariche mobili sono indicate semplicemente con un + (lacune) e con un (elettroni).
FIG. 11. - Rappresentazione
di una giunzione PN, all'atto
della sua formazIone;
le frecce in corrispondenza
della giunzione indicano la
direzione dello spostamento
delle cariche mobili (elettroni
e lacune).
16
Non appena si forma la giunzione, nella regione immediatamente adiacente ad essa si ha una
diffusione spontanea di elettroni dal Ge di tipo N verso il Ge di tipo P e di lacune in senso
inverso; in pratica gli elettroni e le lacune che si trovano nella zona della giunzione si eliminano
gli uni con le altre, nel senso che gli elettroni neutralizzano le lacune. Una volta avvenuto, sempre
nella regione immediatamente adiacente alla superficie di separazione dei due pezzi di
semiconduttore di diverso tipo, il passaggio di cariche mobili nei due sensi opposti,
i due pezzi di materiale non sono più elettricamente neutri.
17
Infatti Ge di tipo P che ha perduto delle
lacune, assume una netta carica negativa,
mentre il Ge di tipo N che ha perduto degli
elettroni, assume una netta carica positiva
(fig. 12). La presenza di cariche negative e
di cariche positive rispettivamente nel Ge P
e nel Ge N, da luogo alla formazione di una
differenza di potenziale o barriera di
potenziale di polarità tale da impedire
l'ulteriore diffusione degli elettroni nella
regione di tipo P e delle lacune in quella di
tipo N. L'arresto della diffusione di elettroni
verso il Ge tipo P e di lacune verso il Ge
tipo N si può spiegare in maniera
elementare. Infatti l'ulteriore passaggio di
elettroni attraverso la giunzione è
ostacolato dalla distribuzione di carica fissa
negativa (accettori) e analogamente le
lacune non diffondono verso il Ge tipo N
essendo respinte dalla distribuzione di
carica fissa positiva (donatori).
FIG. 12. - (a) situazione delle cariche di una giunzione dopo la diffusione delle cariche mobili; la zona
compresa tra i tratteggi e detta zona di svuotamento, o di transizione. Ei rappresenta il campo elettrico
dovuto alla distribuzione di cariche negative e positive nella regione di transizione; (b) andamento della
densità di carica; (c) andamento del potenziale.
18
In fig. 12 sono riportati gli andamenti
della densità di carica e del potenziale
lungo il materiale, la barriera di
potenziale è dovuta alla distribuzione di
cariche nell'adiacenza della giunzione ed
è indicata in fig. 12 (c) con V0.
La regione svuotata di cariche mobili
viene denominata regione di transizione o
di svuotamento (depletion-layer).
FIG. 12. - (a) situazione delle cariche di una giunzione dopo la diffusione delle cariche mobili; la zona
compresa tra i tratteggi e detta zona di svuotamento, o di transizione. Ei rappresenta il campo elettrico
dovuto alla distribuzione di cariche negative e positive nella regione di transizione; (b) andamento della
densità di carica; (c) andamento del potenziale.
19
Giunzione PN sottoposta a un campo elettrico esterno.
La giunzione PN, dopo la diffusione delle cariche mobili nella regione immediatamente
adiacente ad essa, resta nelle condizioni rappresentate in fig. 12. La distribuzione non uniforme di
cariche, donatori ed accettori, da luogo ad un campo elettrico Ei che si oppone al passaggio degli
elettroni liberi verso il Ge di tipo P e delle lacune verso il Ge di tipo N. Si applichi ora una d.d.p.,
ad esempio mediante una batteria, collegata con le polarità indicate in fig. 13 e cioè con il polo
negativo dalla parte del Ge di tipo N. La giunzione viene così sottoposta ad un campo elettrico
esterno E di senso opposto ad Ei; il campo elettrico E ripristina ed agevola la diffusione delle
cariche attraverso la giunzione per cui gli elettroni riprendono a passare dalla regione N alla
regione P e analogamente le lacune vanno dalla regione P verso la regione N. Si stabilisce quindi
una corrente, all'interno del semiconduttore e nel circuito esterno, di intensità I, dipendente dal
valore della tensione esterna applicata.
La giunzione è stata polarizzata in
senso diretto cioè in modo tale da
permettere il passaggio della
corrente. La presenza della tensione
esterna V ha abbassato la barriera di
potenziale, che si opponeva al
passaggio della corrente.
FIG. 13. - Giunzione polarizzata direttamente
20
In maniera più intuitiva si può spiegare il passaggio della corrente, quando si applica una d.d.p.
esterna V con le polarità segnate sempre in fig. 13 col fatto che gli elettroni della regione N, che
venivano respinti dalla distribuzione di cariche fisse negative (accettori), localizzate nella zona di
transizione lato P, ora vengono attirate e sollecitate ad attraversare la giunzione dalla polarità
positiva della batteria. Analogamente le lacune che venivano respinte dalla distribuzione di
cariche fisse positive (donatori), localizzate nella zona di transizione lato N, ora vengono attirate
e portate ad attraversare la giunzione dalla polarità negativa della batteria.
21
Giunzione non conduttrice.
Si invertano ora le polarità della batteria; in questo caso il campo elettrico esterno E ha lo
stesso senso del campo interno Ei che quindi viene rinforzato (fig. 14). In tal modo gli elettroni
liberi della regione N non possono in queste condizioni diffondersi verso la regione P e allo
stesso modo le lacune della regione P non possono diffondersi verso la regione N. Il risultato è
che la giunzione non conduce; si dice che la giunzione è polarizzata in senso inverso; cioè in
modo tale da non permettere la conduzione di corrente. La barriera di potenziale si è innalzata e
la zona di transizione si è allargata In maniera intuitiva si può pure spiegare l'impossibilità delle
cariche libere a superare la giunzione. Infatti gli elettroni della regione N, che venivano respinti
dalla distribuzione di cariche fisse negative (accettori),
localizzate nella zona di transizione
lato P, ora trovano un ulteriore
ostacolo costituito dall'effetto di
repulsione dovuto al polo negativo
della batteria collegato al Ge tipo P.
Con lo stesso ragionamento le lacune
che venivano respinte dalla
distribuzione di cariche fisse positive
(donatori), localizzate nella zona di
transizione lato N, ora trovano
anch'esse un ulteriore ostacolo dovuto
alla repulsione causata dal polo
positivo della batteria, collegato al Ge
tipo N (fig. 14).
FIG. 14. - Giunzione polarizzata inversamente. Nella
figura non sono rappresentati i portatori minoritari.
22
Corrente inverse in una giunzione.
In realtà però anche quando una giunzione è polarizzata inversamente, nel circuito scorre una
debolissima corrente. Nelle figg. 11, 12, 13 e 14 sono stati rappresentati solo gli elettroni e le
lacune liberi dovuti agli atomi di impurità. Non è stato tenuto conto nel ragionamento precedente
e nelle figg. 11, 12, 13 e 14 delle lacune e degli elettroni provenienti dalla rottura dei legami
covalenti degli atomi che formano il reticolo cristallino del germanio, dovuta all'agitazione
termica. Come conseguenza nel pezzo di Ge di tipo N, sarà sempre presente una piccola quantità
di lacune mobili, in numero proporzionale alla temperatura ambiente. Lo stesso ragionamento
porta ad ammettere in un pezzo di Ge di tipo P, la presenza di una piccola quantità di elettroni
mobili. La debole corrente inversa che scorre nel circuito quando la giunzione è polarizzata
inversamente è dovuta proprio a queste cariche mobili, elettroni liberi nel Ge tipo P e lacune
libere nel Ge tipo N, di origine termica, detti portatori di minoranza.
Dalla fig. 15 si può vedere
FIG. 15. - Corrente inverse in una giunzione polarizzata inversamente.
che il campo elettrico esterno E
permette ad alcuni elettroni liberi
della regione P di passare nel Ge
N e ad alcune lacune libere della
regione N di passare nel Ge P.
Poiché il numero di queste
cariche cresce con la
temperatura, la corrente inversa
risulta dipendere da
quest’ultima.
23
Capacità di transizione CT e di diffusione CD.
La regione di transizione presenta una distribuzione di cariche elettriche immobili, costituite dagli
ioni degli elementi donatori e da quelli degli elementi accettori. Queste cariche elettriche
immobili occupano posizioni fisse ben determinate, che non possono abbandonare. Inoltre, come
già detto, nella regione di transizione non è presente alcuna carica mobile e si può considerare
quindi questa zona come un perfetto isolante. Si può perciò definire una capacità caratteristica
della giunzione avente come dielettrico lo spessore della zona di transizione il valore della
capacità e dato dall'espressione:
(12)
dove S è l'area della giunzione, w lo spessore della regione di transizione ed ε la costante
dielettrica del materiale.
Poichè la regione di transizione aumenta il suo spessore w all'aumentare della tensione inversa
applicata, la capacità di transizione CT diminuisce. Praticamente CT varia da alcuni pF a qualche
decina di pF.
Quando la giunzione viene polarizzata in senso diretto, la barriera di potenziale si abbassa e
gli elettroni vanno per diffusione dalla regione N alla regione P, mentre le lacune vanno, sempre
per diffusione, da P ad N. Le lacune iniettate nella zona N, come pure gli elettroni iniettati nella
zona P hanno forte probabilità di ricombinarsi con i portatori di maggioranza esistenti nelle
regioni in cui vengono iniettati.
24
Di conseguenza le concentrazioni delle lacune nella zona N e degli elettroni nella zona P
diminuiscono esponenzialmente con la distanza dalla giunzione stessa. La presenza di cariche non
uniformemente distribuite da luogo ad una capacità, detta capacità di diffusione CD la cui
espressione, che non si intende dimostrare, vale:
(13)
dove Ip e In, sono rispettivamente la corrente delle lacune e la corrente degli elettroni in
conduzione diretta, Dp e Dn le costanti di diffusione delle lacune e degli elettroni (in m2 sec-1) e
infine Lp e Ln le distanze medie che le lacune e gli elettroni percorrono prima della
ricombinazione.
25
Leggi dell'azione di massa e di neutralità elettrica.
Siano n e p rispettivamente le concentrazioni degli elettroni e delle lacune in un semiconduttore
drogato ed ni la concentrazione intrinseca definita nel paragrafo “Resistività intrinseca dei
semiconduttori”. Tra queste grandezze sussite la relazione detta dell'azione di massa:
(14)
Nel caso di un semiconduttore intrinseco è, come già visto, n = p = ni.
In un semiconduttore drogato sia con impurezze donatrici, che con impurezze accettrici,
indichiamo con ND la concentrazione degli atomi donatori; poiché essi in seno al cristallo
diventano ioni positivi, la densità di carica positiva totale nel semiconduttore è: (ND + p)· e.
Analogamente indichiamo con NA la concentrazione degli atomi accettori; poiché questi in seno
al cristallo diventano ioni negativi, la densità di carica negativa totale è: (NA + n)· e.
Essendo il semiconduttore nel suo complesso elettricamente neutro, la densità di carica
positiva deve essere uguale a quella negativa totale, quindi si può scrivere:
(15)
che esprime appunto la legge di neutralità elettrica.
26
Dalle (14) e (15) si possono ricavare, per un semiconduttore drogato sia con impurezze donatrici
sia con impurezze accettrici, le concentrazioni dei portatori n e p, note le concentrazioni ND , NA
e ni. Sia dato ora un semiconduttore di tipo N, in cui cioè siano presenti solo impurezze donatrici;
in questo caso è NA = 0. Poiché in un semiconduttore di tipo N il numero di elettroni liberi è
molto più grande di quello delle lacune, cioè n >> p, la (15) si riduce quindi a:
(16)
cioè la concentrazione degli elettroni liberi è all'incirca uguale alla densità degli atomi donatori.
Dalla (14) tenendo conto della (16) si può ricavare la concentrazione delle lacune:
(17)
(Il pedice n sta a ricordare che nn e pn sono le concentrazioni rispettivamente di elettroni e di
lacune in materiale di tipo N).
Con lo stesso ragionamento in un semiconduttore di tipo P per il quale sia ND = 0, poichè è
p >> n, si ha:
(18)
(19)
Anche qui il pedice p sta ad indicare che le concentrazioni np e pp sono quelle relative ad un
materiale di tipo P.
In un semiconduttore il prodotto n·p è costante ad una prefissata temperatura e poiché la
concentrazione intrinseca ni è piccola, bastano concentrazioni minime di impurezze per 27
sbilanciare notevolmente le concentrazioni dei portatori.
Esempio:
In un cristallo di silicio la concentrazione degli atomi di Si è di circa 10-23 cm-3; un atomo di
impurezze donatrici per ogni 108 atomi di Si corrisponde ad una concentrazione di donatori di
1015 cm-3. Poiché il prodotto n·p per il Si a temperatura ambiente è circa 1020 cm-6 si ha dalle (16)
e (17)
La concentrazione d'impurezza donatrice è estremamente piccola, ma ha ugualmente un
grandissimo effetto sulla concentrazione dei portatori e in definitiva sulle proprietà elettriche
del semiconduttore.
28
Resistività dei semiconduttori drogati.
Nei semiconduttori drogati si è visto che valgono le relazioni (16) e (18), cioè la resistività
dipende in pratica dalle sole cariche maggioritarie, pertanto si può scrivere:
(20)
(21)
Le (20) e (21) rappresentano rispettivamente la conduttività in un semiconduttore di tipo N ed in
uno di tipo P. I loro inversi costituiscono le resistività dei semiconduttori drogati:
(22)
(23)
La resistività di un semiconduttore drogato cresce all'aumentare della temperatura; infatti la
mobilità dei portatori di maggioranza diminuisce all'aumentare della temperatura, mentre NA ed
ND non dipendono da essa, supponendo che tutti gli atomi di drogante siano ionizzati a
temperatura ambiente.
29
Effetto Hall.
Se una barretta di semiconduttore è percorsa da una corrente I e posta in un campo magnetico
di induzione B trasverso come in fig. 16, si induce in essa un campo elettrico E in direzione
perpendicolare sia a B che a I. Questo fenomeno è noto come effetto Hall e può essere sfruttato
per determinare se un semiconduttore è di tipo N o P e per trovare la concentrazione dei portatori
in esso presenti Mediante una simultanea misura della conducibilità σ è possibile inoltre calcolare
la mobilità µ del portatori.
FIG. 16. - Effetto Hall.
30
L'effetto Hall si può spiegare fisicamente come segue. Con le direzioni di B e di I indicate in
figura, si esercita sui portatori una forza, dovuta al campo magnetico, in direzione perpendicolare
al piano individuato da I e da B. Se il semiconduttore è di tipo N, nel quale la corrente è prodotta
da elettroni, quest'ultimi sono soggetti ad una forza diretta verso l'alto e spinti verso il lato 1 della
barretta, che si carica quindi negativamente rispetto al lato 2. Fra le superfici 1 e 2 appare allora
una differenza di potenziale VH , detta tensione di Hall. In condizioni di equilibrio l'intensità del
campo elettrico E dovuto all'effetto Hall deve esercitare sulle cariche una forza tale da bilanciare
la forza dovuta al campo magnetico (forza di Lorentz), cioè si ha:
(24)
in cui e è la carica dell'elettrone, u la velocità di scorrimento (drift) dei portatori di corrente.
Supponendo il campo elettrico uniforme, risulta: E =VH / d, J = δ · u = I / (w ·d), dove J è la
densità di corrente, δ la densità di carica e w la dimensione indicata in fig. 16.
Combinando queste
relazioni con la (24) si
ottiene:
(25)
FIG. 16. - Effetto Hall.
31
Misurando VH , B, I e w si può determinare la densità di carica δ. Se la polarità di VH è positiva al
terminale 2, allora i portatori sono elettroni ed il materiale è di tipo N; dalla relazione δ = n·e si
può calcolare la concentrazione n. Se invece il terminale 1 è positivo rispetto a quello 2, i
portatori sono cariche positive (lacune) ed il semiconduttore è di tipo P; dalla relazione δ = p·e è
possibile calcolare la concentrazione p delle lacune.
Si definisce infine costante di Hall RH la grandezza:
(26)
32
Giunzione PN: concentrazioni delle cariche mobili, correnti di drift e di diffusione.
Polarizzazione diretta.
Riprendiamo il caso di una giunzione PN polarizzata in senso diretto per esaminare più
dettagliatamente la natura della corrente totale, che scorre nel semiconduttore.
Si considera una giunzione asimmetrica, in cui cioè il semiconduttore di tipo P abbia una forte
concentrazione di accettori ed il semiconduttore di tipo N abbia invece una moderata
concentrazione di donatori. Poiché la polarizzazione della giunzione è diretta, le lacune della
regione P si spostano continuamente verso la giunzione, per effetto del gradiente di potenziale
(campo elettrico esterno E) che si stabilisce lungo il semiconduttore P (cioè le lacune si spostano
lungo le linee di forza del campo E, in direzione della regione a potenziale più basso).
Il movimento di queste cariche costituisce una corrente elettrica detta corrente di drift. Le
lacune gradualmente, per effetto dell'agitazione termica, saltano la barriera ed entrano in N, dove
vengono subito a far parte delle cariche minoritarie. Si dice che le cariche che attraversano la
barriera sono emesse dalla giunzione. Le lacune che hanno così attraversato la barriera, una volta
allontanatesi dalla regione di transizione, si ricombinano con gli elettroni esistenti, con
conseguente diminuzione graduale della concentrazione delle lacune stesse; in fig. 17 è
rappresentata la curva pn(x) e np(x) della concentrazione delle cariche minoritarie; la variazione
della concentrazione delle cariche maggioritarie pp e nn è così piccola da non potersi
rappresentare e perciò essa appare costante sia lungo il semiconduttore di tipo N che lungo quello
di tipo P. Si origina cosi un gradiente di concentrazione, che da luogo ad una corrente di
diffusione. La velocità con cui si diffondono le lacune nella regione N e quindi il valore della
corrente di diffusione dipende dall'entità del gradiente di diffusione, cioè dalla pendenza della
33
curva della concentrazione.
Il fenomeno è simile a
quello di diffusione di un
gas che, passando da un
ambiente a più elevata
concentrazione (pressione)
ad un ambiente a più bassa
concentrazione, si espande
con una velocità
proporzionale al salto di
pressione. Come si può
vedere dalla fig. 17 (a) ad
una certa distanza dalla
giunzione, tutte le lacune
iniettate nel materiale N
sono, praticamente,
scomparse, per effetto delle
ricombinazioni con gli
elettroni ivi esistenti.
FIG. 17. - Giunzione polarizzata
direttamente; (a) andamento della
densità dei portatori di maggioranza
[lacuna pp nel GeP ed elettroni nn nel
GeN] e dei portatori di minoranza
[elettroni np(x) nel GeP e lacuna pn(x)
nel GeN]; (b) componentl della34
corrente lungo il semiconduttore.
Analogamente nella regione N gli elettroni si spostano verso la giunzione per effetto del
gradiente di potenziale che si ha lungo il semiconduttore N. Una volta attraversata la giunzione,
gli elettroni si trovano a far parte delle cariche minoritarie del semiconduttore P, in cui si
diffondono allontanandosi dalla regione di transizione; gli elettroni si ricombinano con le lacune
presenti qui in gran numero. Di conseguenza la concentrazione degli elettroni decresce
allontanandosi dalla giunzione, dando luogo ad un gradiente di concentrazione, da cui dipende
l'entità della corrente di diffusione (fig. 17 b), che è massima ancora una volta nei pressi della
giunzione.
Nel caso in esame, poiché la giunzione è asimmetrica, essa è attraversata da un quantitativo di
lacune superiore a quello degli elettroni e di conseguenza la corrente di diffusione sarà più
elevata nel semiconduttore di tipo N. Sia le lacune che gli elettroni sono dei portatori di carica
elettrica quindi la corrente che attraversa una qualunque sezione trasversale del semiconduttore è
data dalla somma della corrente di drift dovuta alle cariche maggioritarie e della corrente di
diffusione dovuta alle cariche minoritarie. Poiché il valore della corrente elettrica totale risultante
deve essere uguale in ogni sezione trasversale del semiconduttore, le due componenti della
corrente sono complementari.
35
Polarizzazione inversa.
Si è visto che nel caso di giunzione polarizzata inversamente si ha una debole corrente
inversa dovuta alla presenza dei portatori minoritari, elettroni e lacune, prodotti per effetto
dell'agitazione termica. Infatti alcuni elettroni minoritari della regione P, per effetto del
movimento di diffusione giungono nei pressi della giunzione; il campo elettrico ivi esistente li fa
passare nella regione N.
Come conseguenza dell'asportazione di elettroni dalla regione P, la loro concentrazione
all'interno di questa regione varia secondo l'andamento esponenziale np(x) mostrato in fig. 18.
Si ha un gradiente di concentrazione che favorisce la diffusione verso la giunzione degli
elettroni minoritari presenti nel semiconduttore P.
Una volta che questi elettroni minoritari sono passati nella regione N, essi si mescolano con
gli elettroni maggioritari qui esistenti e si allontanano dalla giunzione per effetto di un leggero
gradiente di potenziale dovuto alla polarizzazione esterna; il movimento di questi elettroni
costituisce una corrente di drift lungo il semiconduttore di tipo N. Analogamente alcune lacune
minoritarie della regione N sempre a causa della diffusione spontanea pervengono in vicinanza
della giunzione e vengono proiettati per effetto del campo elettrico di barriera nella regione di
tipo P. In questa regione le lacune minoritarie si mescolano con le lacune maggioritarie ivi
esistenti, dando luogo, muovendosi lungo P, ad una corrente di drift sempre per effetto del
leggero gradiente di potenziale dovuto alla polarizzazione esterna. Si ha nella regione N un
gradiente di concentrazione di lacune. In figura 18 (a) è riportato l'andamento della
concentrazione degli elettroni, sempre di tipo esponenziale, pn(x).
36
Gli andamenti delle
correnti all'interno del
semiconduttore sono
mostrati in fig. 18 (b);
tali correnti hanno natura
e andamento simili a
quelli già riscontrati nel
caso di polarizzazione
diretta.
La differenza
fondamentale tra
giunzione polarizzata
direttamente e giunzione
polarizzata inversamente
consiste, oltre al fatto
che qui le cariche si
muovono in direzioni
opposte alle precedenti,
nell'intensità della
corrente che è molto
piccola.
FIG. 18. - Giunzione polarizzata inversamente: (a) andamento della densità del portatori di
maggioranza [lacune pp nel GeP ed elettroni nn nel GeN] e dei portatori di minoranza [elettroni
np (x) nel GeP e lacune pn (x) nel GeN]; (b) componenti della corrente lungo il semiconduttore
37
Infatti con la polarizzazione inversa la barriera di potenziale si è elevata e le cariche maggioritarie
non partecipano in pratica alla conduzione; le correnti sono dovute soltanto allo scarso numero di
cariche minoritarie, che si portano verso la giunzione per effetto del gradiente di concentrazione
originato spontaneamente, col meccanismo sopra descritto.
38