Ottica fisica e ottica ondulatoria
La luce è un’onda elettromagnetica; ne studiamo le proprietà
principali, tra cui quelle non dipendenti direttamente dalla
natura ondulatoria (ottica “geometrica”)
Lezione 12
Vedi anche:
“Natura e storia della luce”
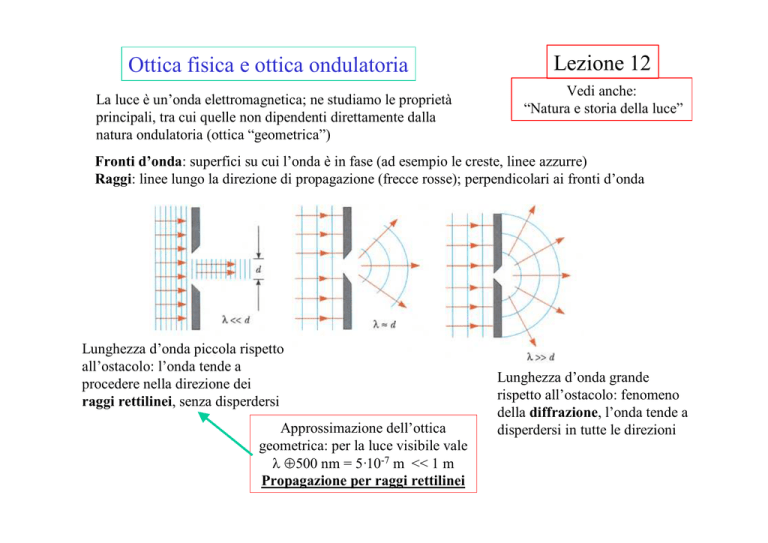
Fronti d’onda: superfici su cui l’onda è in fase (ad esempio le creste, linee azzurre)
Raggi: linee lungo la direzione di propagazione (frecce rosse); perpendicolari ai fronti d’onda
Lunghezza d’onda piccola rispetto
all’ostacolo: l’onda tende a
procedere nella direzione dei
raggi rettilinei, senza disperdersi
Approssimazione dell’ottica
geometrica: per la luce visibile vale
λ ≈ 500 nm = 5·10-7 m << 1 m
Propagazione per raggi rettilinei
Lunghezza d’onda grande
rispetto all’ostacolo: fenomeno
della diffrazione, l’onda tende a
disperdersi in tutte le direzioni
normale alla sup.
Riflessione
raggio incidente
Su superfici lisce il raggio luminoso subisce riflessione;
considerando gli angoli rispetto alla normale alla superficie
nel punto di incidenza del raggio
θi = θr
raggio riflesso
θi θ
r
angolo di incidenza = angolo di riflessione
raggio incidente
Rifrazione
Quando un raggio incide sulla superficie di separazione tra due
mezzi (trasparenti) diversi, in cui la velocità di propagazione è
diversa, si ha una deviazione della direzione di propagazione; i raggi
stanno sullo stesso piano perpendicolare alla superficie, e vale la
Legge di Snell
della rifrazione
θ1
sin(θ1 ) v1
=
sin(θ 2 ) v 2
normale
1
2
θ2
raggio rifratto
dove v1 e v2 sono le velocità del raggio nei mezzi 1 e 2
raggio più lento → traiettoria più vicina alla normale (e viceversa)
La frequenza dell’onda rimane invariata (le vibrazioni sulla
superficie di separazione sono le stesse)
La lunghezza d’onda diminuisce se v diminuisce (da v = λ · ν),
o aumenta se v aumenta
sen(θ1)
r=1
sen(θ2)
Definizione: indice di rifrazione
c
n = ≥1
v
velocità della luce nel vuoto
velocità della luce nel mezzo
Legge di Snell:
n1 ⋅ sin(θ1 ) = n2 ⋅ sin(θ 2 )
Indice di rifrazione più grande → traiettoria
più vicina alla normale (e viceversa)
v sempre minore o uguale a c, la quale è la
massima velocità possibile (relatività di Einstein)
n è una proprietà fondamentale
dei mezzi materiali trasparenti
(e più misurabile rispetto alla v!)
Esempi: vuoto n = 1; aria n = 1.0003;
acqua n = 1.33, semiconduttori n = 3.6;
eccetera…
Prisma di vetro che rifrange un raggio di luce
monocromatico, e lo devia di un angolo δ
L’indice di rifrazione n può variare con
la lunghezza d’onda: onde luminose di
lunghezza d’onda maggiore hanno n
minore e viceversa. Fenomeno della
dispersione: un raggio di luce “bianca”
(che contiene tutte le lunghezze d’onda
nella regione visibile) viene separato nei
vari raggi componenti (i colori)
La componente “blu” della luce bianca
viene deviata più della componente “rossa”
normale
Riflessione totale
Quando un raggio passa da un mezzo di indice di
rifrazione maggiore a uno con indice di rifrazione
minore, l’angolo di uscita (rispetto alla normale) è
maggiore dell’angolo di incidenza.
Il valore massimo di θ2 è π/2; a questo corrisponde
l’angolo di incidenza θL che si ricava da
n1 ⋅ sin(θ L ) = n2 ⋅ sin(π / 2)
sin(θ L ) =
aria
n1 > n2
n2
(< 1)
n1
θL
Un raggio incidente con l’angolo θL , detto angolo
limite, esce parallelo alla superficie (raggio 4).
Un raggio incidente con un angolo θi maggiore di θL
(raggio 5) , non può uscire e viene riflesso nel mezzo 1.
acqua
Quindi passando da n1 a n2 , con n1 > n2 , se l’angolo di
incidenza è abbastanza grande il raggio rimane confinato nel
mezzo. Questo fenomeno è sfruttato ad esempio nelle fibre
ottiche (in vetro), che trasportano luce senza disperderla.
Relazione tra indice di rifrazione e costante dielettrica relativa
In un mezzo materiale (dielettrico):
ε = ε r ⋅ε 0
Costante dielettrica
Permeabilità magnetica µ ≅ µ 0
Velocità delle luce nel mezzo
v=
1
εµ
=
1
ε rε 0 µ0
=
c
εr
Indice di rifrazione
n=
c
= εr
v
x
Ex
E x = E0 cos(θ ) (propagante)
E y = E0 sin(θ ) ( viene assorbita )
Se I0 è l’intensità dell’onda
all’ingresso del materiale,
l’intensità all’uscita I1 è
data dalla legge di Malus:
I1 = I 0 ⋅ cos 2 (θ )
I 0 ∝ E02
I1 ∝ E x2
Luce non polarizzata
(campo E in tutte le direzioni)
La luce emessa da sorgenti estese
(molti atomi) è composta da molte
onde e non è polarizzata, cioè non ha
una direzione preferenziale di
polarizzazione
θ
Direzione dell’onda
polarizzazione su y
Ey
z
E0
y
y
polarizzazione su x
Il materiale fissa le direzioni x (di
passaggio) e y (di assorbimento)
Se l’onda incidente sul materiale
oscilla con ampiezze E0 nella
direzione ad angolo θ rispetto a x,
la componente dell’oscillazione
sull’asse y viene assorbita, la
componente sull’asse x passa.
I1
Le ampiezze
dell’onda sono:
x
Direzione in cui oscilla il campo
elettrico dell’onda luminosa
Polarizzazione della luce
Esistono materiali (naturali e artificiali
come il polaroid) che polarizzano la luce,
assorbendo le vibrazioni del campo in
una direzione e lasciando passare quelle
nella direzione ortogonale
Luce non polarizzata che incide su un
polarizzatore: l’energia (o l’intensità) si
ripartisce equamente sulle due direzioni
ortogonali x e y, quindi →
luce non
polarizz.
I1 =
I0
2
x
lente
polarizzatrice
luce polarizzata x
I0
z
I1
Luce polarizzata che incide su un polarizzatore, il
cui asse x è inclinato dell’angolo θ rispetto alla
direzione di polarizzazione incidente.
θ
I1 = I 0 ⋅ cos 2 (θ )
Se la luce polarizzata è generata da un primo
polarizzatore, la luce uscente dal secondo polarizzatore
è massima per θ = 0 (polarizzatori paralleli)
è minima (zero!) per θ = π/2 (polarizzatori incrociati)
Generazione di luce polarizzata
a)
b)
c)
Per mezzo di lenti polarizzanti (come sopra).
Per riflessione: legge di Brewster, se i raggi riflesso e rifratto sono
tra loro perpendicolari, la luce riflessa è completamente polarizzata
perpendicolare al piano di incidenza. →
Per rifrazione: fenomeno della birifrangenza. Certi cristalli
generano due raggi rifratti in direzioni diverse (perché la luce ha
velocità diverse nelle diverse direzioni del reticolo cristallino) e
questi raggi sono polarizzati in direzioni ortogonali.
I0
z
I1
Interferenza di onde luminose
Si hanno fenomeni di interferenza (che rendono evidente la natura ondulatoria della luce) quando:
a) Si sovrappongono onde emesse da sorgenti coerenti, cioè che hanno una differenza di fase
ben definita (esempio: se si usa la stessa lampadina)
b) Se sono onde monocromatiche, cioè con la stessa lunghezza d’onda (esempio: si seleziona
un raggio uscente da un prisma, o emesso da un laser)
Esperimento di Young (1801)
Una lampada illumina, con luce
monocromatica, la piccola fenditura
S0, che fa da sorgente che illumina le
due fenditure S1 e S2. Queste
costituiscono due sorgenti di luce
coerenti (onde sinusoidali in fase).
Sullo schermo si osservano frange
alternate chiare e scure, originate
dall’interferenza delle onde
luminose provenienti da S1 e S2.
(sovrapposizione di onde sinusoidali
→ ampiezza totale da zero a un massimo)
Interferenza costruttiva se δ corrisponde a un
numero intero di lunghezze d’onda (frange luminose)
δ = m⋅λ
(con m intero qualsiasi)
Interferenza distruttiva se δ corrisponde a una
mezza lunghezza d’onda in più (frange scure)
δ = m+
posizione dei massimi luminosi:
sin(θ ) =
m⋅λ y
=
d
L
y=m
λ⋅L
d
posizione dei
minimi (buio):
1
⋅λ
2
1 λ⋅L
2 d
y
L
come si vede dalla figura; inoltre sin(θ ) ≅ tan(θ ) =
δ = r2 − r1 = d sin(θ )
d distanza tra le fenditure (≈ mm)
L >> d distanza (orizzontale) dello schermo
y posizione di P sull’asse verticale dello schermo
θ angolo della direzione di P rispetto
all’orizzontale (a metà tra le fenditure)
S1 e S2 emettono onde uguali (A, ω, k uguali)
e in fase (ad esempio, in S1 e S2 e in un certo
istante le due onde sono all’ampiezza massima).
Sul punto P arrivano:
1) l’onda di S1 che ha percorso r1
2) l’onda di S2 che ha percorso r2
Dato che r2 > r1 la seconda onda è in
ritardo, e non è più in fase con la prima; il
risultato della sovrapposizione di queste
onde sinusoidali dipende da:
Differenza di cammino ottico
y = m+
Intensità della figura di interferenza: dalla sovrapposizione
di onde sinusoidali sappiamo che il campo elettrico totale
dell’onda e.m. risultante è
E1
ET = E1 + E2 = 2 E0 ⋅ cos(ϕ / 2) ⋅ sin (kx − ωt + ϕ / 2)
Ampiezza risultante
E2
Onda sinusoidale risultante
La differenza di fase delle onde ϕ dipende
2π d y
k
k
d
=
⋅
=
⋅
sin(
)
=
ϕ
δ
θ
dalla differenza di cammino ottico:
I in funzione di δ
λL
L’ intensità di illuminazione è proporzionale al
campo elettrico al quadrato, quindi si avrà:
I = I 0 cos 2 (ϕ / 2)
δ
Cambiamento di fase dovuto alla riflessione
Un’onda elettromagnetica (quindi anche la
luce) subisce un cambiamento di fase di π rad
(1800) se riflessa da un mezzo con indice di
rifrazione più alto. Nel caso opposto non si
verifica nessuna variazione di fase (e neppure
se l’onda subisce rifrazione).
Questo fenomeno è importante per →
Supporto rigido
sin(kx − ωt + π )
sin(kx − ωt )
sin( kx − ωt )
1
n1 < n2
2
Analogia con
un’onda su una corda
Interferenza di lamine sottili
Es. bolle di sapone, olio su acqua, strati antiriflesso,…
interf.
Lamina di spessore d e indice di rifrazione n , su cui incide quasi
perpendicolarmente un raggio luminoso di lunghezza d’onda in aria
λ = c/ν. Dato che n = c/v (e la frequenza non cambia) la lunghezza
d’onda nel mezzo è λn = v/ν = λ/n (inferiore a quella in aria).
La differenza di cammino ottico tra i due raggi è quindi:
2nd = m+
1
λ
2
δ = 2 d − λn / 2
Interferenza distruttiva se δ corrisponde a una
mezza lunghezza d’onda (nel mezzo) in più
δ = m ⋅ λn
Interferenza costruttiva se δ corrisponde a un
numero intero di lunghezze d’onda (nel mezzo)
2
d
δ = m+
1
λn
2
L’interferenza dipende dallo spessore della lamina e dall’indice di
rifrazione; inoltre dipende dalla lunghezza d’onda. Vengono quindi
osservati massimi e minimi di intensità diversi per ogni colore!
(2)
Raggio riflesso dalla superficie superiore, cambiamento di fase π,
(corrispondente a un cammino ottico di mezza lunghezza d’onda).
Raggio rifratto e riflesso dalla faccia inferiore, nessun
cambiamento di fase; il raggio però viaggia per una ulteriore
distanza 2d nel mezzo, rispetto al raggio in aria.
(1)
1
2nd = m⋅λ
Anelli di Newton
interf.
Lente circolare sottile su un piano di vetro; in
questo caso il ruolo della lamina sottile è svolto
dall’aria interposta tra i due vetri (si ha
cambiamento di fase nella riflessione sul piano di
vetro) Si osservano delle frange circolari,
alternativamente chiare e scure
Diffrazione
d
Condizione per osservare
i fenomeni di diffrazione
λ>d
Si ha diffrazione quando le onde passano
per piccole aperture, o intorno a piccoli
ostacoli. Si ha un allargamento del fronte
d’onda,
ben
oltre
la
normale
propagazione rettilinea. Le immagini
non sono nette (come idealmente sarebbe
per i raggi rettilinei) ma con zone di luce
e di ombra. Vi è un massimo centrale di
intensità luminosa, circondato da
massimi e minimi secondari .
Diffrazione da singola fenditura
Un fronte d’onda (raggio) luminoso incide su una fenditura di dimensione a.
Ogni elemento della fenditura si comporta come una sorgente di onde luminose
in fase tra loro (è il principio di Huygens, un principio fondamentale della
propagazione per onde). Sullo schermo arriva quindi una sovrapposizione di
onde provenienti da ogni punto della fenditura, e si ha interferenza.
Effetto dell’interferenza :
→ Per θ = 0 (e L >> a) le onde percorrono praticamente la stessa distanza,
quindi si ha interferenza costruttiva e il massimo di illuminazione I0 .
→ Per θ > 0, l’intensità diminuisce fino a zero. Per trovare la posizione di
questo minimo, consideriamo la fenditura divisa in due parti uguali (a/2).
Ad ogni onda generata da punto nella metà inferiore corrisponde un’onda
generata da un punto della metà superiore (ad esempio le onde 1 e 3); si ha
interferenza distruttiva se la differenza di cammino ottico è mezza
lunghezza d’onda, da cui la condizione:
λ a
λ
= sin(θ )
sin(θ ) =
2 2
a
→ Un altro minimo si trova in modo analogo
λ a
= sin(θ )
dividendo la fenditura in 4 parti, e così via →
2 4
I0
Condizione per i minimi di intensità
λ
sin(θ ) = m
;
m = ± 1, ± 2,
a
;
m = ± 1, ± 2,
Per angoli piccoli, sin(θ) ≈ θ, quindi
λ
θ =m
la condizione approssimativa
a
La diffrazione limita le capacità degli strumenti ottici di distinguere (“risolvere”)
immagini di oggetti tra loro vicini. Le immagini sono costruite facendo passare la
luce attraverso lenti e/o aperture (esempio le immagini delle due sorgenti quasi
puntiformi S1 e S2 , di separazione angolare θ ) per cui l’immagine non è mai netta
ma costituita da un massimo centrale allargato e “sfuocato”, con altri massimi
secondari di contorno. Per decidere quando due immagini possono dirsi risolte, si
usa la condizione:
θ
Criterio di Rayleigh
Le immagini sono risolte quando il
massimo centrale dell’una coincide
col primo minimo dell’altra.
Figure di diffrazione di due sorgenti
puntiformi, per diverse separazioni angolari
Per aperture rettangolari, il
λ
θ
≅
min
primo minimo si trova a
a
(vedi la pag. precedente) che è quindi
l’angolo minimo con cui possiamo dire di
osservare separati due oggetti (un esempio
si osserva nella figura centrale).
λ
Per aperture circolari, il
θ
≅
1
.
22
min
primo minimo si trova a
a
Si può aumentare la “risoluzione” delle
immagini diminuendo la lunghezza d’onda;
questa è la ragione per cui si sono inventati
il microscopio a raggi X, il microscopio
elettronico etc.
Sorgenti distanti,
immagini ben risolte
Sorgenti molto vicine,
immagini non risolte
Sorgenti vicine,
immagini appena risolte
Reticolo di diffrazione
Utile strumento per misurare la lunghezza d’onda della luce, o
per produrre fasci di luce monocromatica. E’ costituito da N
fenditure (o N righe) sottili ed equispaziate, dell’ordine di
migliaia per cm. Effetti combinati di interferenza e diffrazione.
→ La distanza d tra le fenditure determina l’interferenza delle
onde emesse: come prima, la posizione dei massimi è data da
d sin(θ ) = m ⋅ λ
( m intero )
→ La diffrazione dalla singola fenditura interferisce con
quella delle altre fenditure, e determina un restringimento
delle frange (più efficace più è grande N). Si ha una figura
composta di massimi molto stretti ed equispaziati
Se la sorgente emette diverse lunghezze d’onda (es. luce bianca), ogni
onda ha la sua figura di massimi, ed è possibile selezionare una luce
monocromatica, di lunghezza d’onda fissata a piacere, posizionando P
sull’angolo opportuno.
Potere risolutivo del reticolo
= capacità di “risolvere” tra due lunghezze d’onda diverse
Per definizione R =
λ
λ
= media
∆λ λ1 − λ2
Per il reticolo, in base al criterio di Rayleigh si trova R
Il potere risolutivo è maggiore più è grande il numero
di righe, e per alto ordine dei massimi (grandi angoli).
= N ⋅m
Intensità luminosa in funzione di sin(θ);
m si dice “ordine dei massimi di intensità”
La natura della luce (e delle onde e.m.)
Il modello ondulatorio per le onde e.m. (che deriva direttamente dall Eq. di Maxwell) descrive perfettamente tutti
i fenomeni luminosi. Ma nuovi fenomeni osservati a livello atomico e subatomico, a partire dal 1900, (emissione
di corpo nero, interazioni con elettroni e con la materia etc.) mostrano che la luce può comportarsi anche come
una “particella”. Oggi sappiamo che (almeno per i fenomeni su scala atomica) l’energia luminosa non è continua
(come immaginato nel modello ondulatorio classico), ma è distribuita in pacchetti detti “quanti” o “fotoni”; si
dice che l’energia è quantizzata, e in particolare si ha che l’energia di un fotone è proporzionale alla frequenza
dell’onda corrispondente secondo la legge (di Planck):
E = h ⋅ν
Immagine (non realistica) della propagazione di
onde e.m. in forma di quanti di luce, o fotoni
E = hν
10-34
dove h = 6.626 x
J·s è la “costante di Planck”, caratteristica
della fisica dei fenomeni microscopici a livello atomico.
L’ “intensità” della luce (densità di energia per velocità) può quindi essere
interpretata come “il numero di fotoni N che attraversano l’unità di
superficie e di tempo, moltiplicato per l’energia hν del singolo fotone”
L’aspetto “corpuscolare” della radiazione luminosa implica anche che,
oltre all’energia E, il fotone possiede la quantità di moto p data da →
(la seconda formula si ricava con la relazione fondamentale c = λ ν )
E h
p= =
c λ
Anche per i fotoni valgono sempre le leggi di conservazione dell’Energia e conservazione della quantità di moto
I fotoni possono subire urti elastici o anelastici (leggi degli urti come per le particelle), scambiando energia e
quantità di moto, e quindi con variazioni di frequenza e lunghezza d’onda. Oppure possono essere assorbiti o
emessi; in questo caso l’energia e la quantità di moto vengono cedute (o prelevate) completamente al materiale.
luce
Effetto fotoelettrico
Quando la luce incide sulla superficie metallica A si ha emissione di
elettroni, che possono raggiungere la placca B e determinare una
corrente nel circuito. L’energia cinetica dei fotoelettroni viene misurata
rallentandoli per mezzo di una differenza di potenziale contraria: quando
la corrente cade a zero, il potenziale (detto potenziale di arresto V0) è
uguale all’energia cinetica massima degli elettroni emessi:
K MAX = qe ⋅ V0
A
Elettroni
(energia KMAX)
+
B
−
Le osservazioni sperimentali ci dicono che:
1)
Si ha emissione di elettroni solo se la frequenza della luce incidente è
Differenza di
superiore a una frequenza di soglia (caratteristica del materiale);
potenziale variabile V0
2)
il numero degli elettroni emessi è proporzionale all’intensità della luce;
3)
l’energia cinetica massima degli elettroni non dipende dall’intensità ma
solo dalla frequenza della luce (crescente con essa).
La teoria ondulatoria non è in grado di spiegare questi fatti, mentre trattando la luce come una corrente di
fotoni, il fenomeno è spiegato come l’assorbimento di un fotone da parte di un elettrone del metallo, con
cessione di tutta l’energia. Infatti si ha che:
1)
per estrarre un elettrone da un metallo è necessaria un’energia minima φ
K MAX
(energia di estrazione o di ionizzazione). A questa corrisponde un fotone
di frequenza minima ν 0 = φ / h, al di sotto della quale non è possibile
estrarre l’elettrone dal materiale, qualunque sia l’intensità luminosa;
2)
il numero di elettroni emessi sarà proporzionale al numero dei fotoni
incidenti, e quindi all’intensità;
3)
l’energia cinetica massima si trova dal bilancio energetico: K
MAX = hν − φ
0 ν0
e quindi dipende dalla frequenza, e si ha energia cinetica
maggiore per frequenze incidenti maggiori (vedi il grafico).
ν












