Area dei poligoni

POLIGONI
RETTANGOLO
Il rettangolo è un parallelogramma che ha gli angoli congruenti.
● Ha le diagonali congruenti
Pertanto ogni parallelogramma che ha gli angoli congruenti e le diagonali congruenti è un
rettangolo.
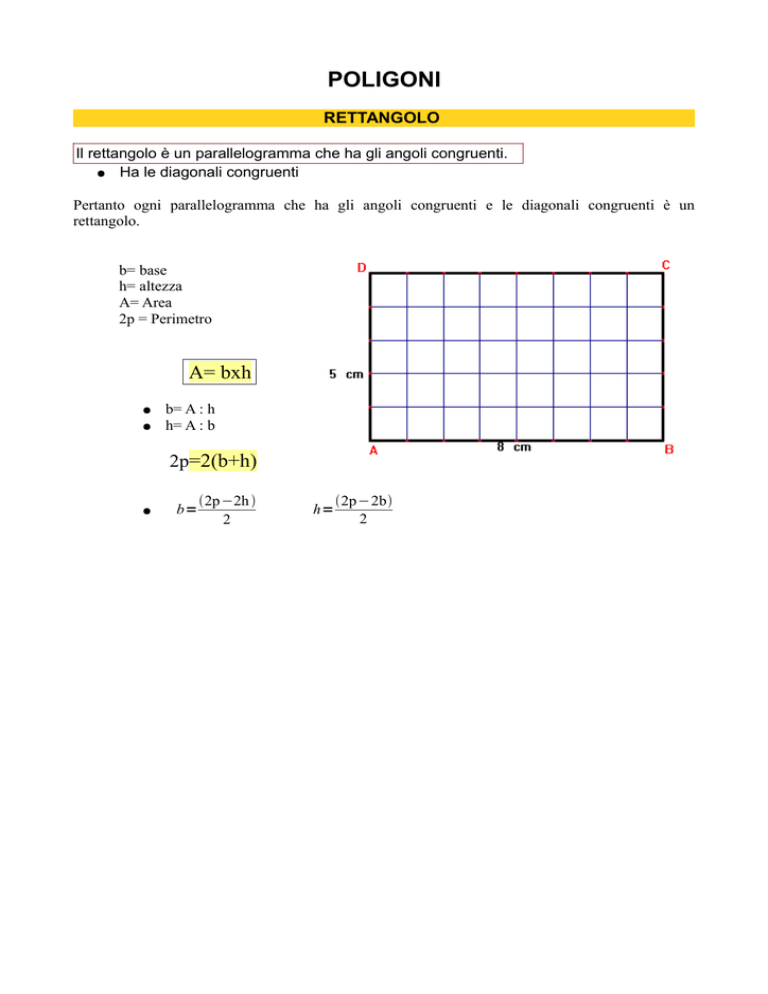
b= base
h= altezza
A= Area
2p = Perimetro
A= bxh
●
●
b= A : h
h= A : b
2p=2(b+h)
●
b=
2p−2h 
2
h=
2p−2b
2
PARALLELOGRAMMA
Il parallelogramma è un quadrilatero avente i lati opposti paralleli.
● Ha le diagonali congruenti che si tagliano a metà
● Ha i lati opposti congruenti
● Ha gli angoli a due a due supplementari, quelli consecutivi.
● Ha gli angoli opposti congruenti
Osserva
Il Parallelogramma è equivalente ad un rettangolo avente la stessa base e la stessa altezza
del parallelogramma dato. Quindi l'area del parallelogramma si calcola come quella del
rettangolo.
AB=b
HD=h
A= Area
A= bxh
●
●
b= A : h
h= A : b
Il Parallelogramma ha due basi e due altezze e quindi ABxHD = ADxBK
TRIANGOLO
Il triangolo è un poligono avente tre lati e tre angoli.
•
La somma degli angoli interni è 180°
•
Ciascun lato è minore della somma degli altri due ed è maggiore della differenza
degli altri due
Al lato maggiore si oppone l'angolo maggiore e al lato minore si oppone l'angolo
minore e viceversa.
•
•
•
•
•
•
•
•
•
•
•
Un triangolo è isoscele se ha due lati congruenti
Un triangolo è equilatero se ha i tre lati congruenti
Un triangolo è rettangolo se ha un angolo retto
Un triangolo è acutangolo se ha gli angoli acuti
Un triangolo è ottusangolo se ha un angolo ottuso
Un triangolo è scaleno se ha i lati diversi
Un triangolo rettangolo può essere isoscele e scaleno
Un triangolo acutangolo può essere isoscele, equilatero e scaleno
Un triangolo ottusangolo può essere isoscele e scaleno
In un triangolo si chiama:
•
Ortocentro il punto di intersezione delle tre altezze
•
Circocentro il punto di intersezione degli assi relativi ai lati
•
Incentro il punto di intersezione delle bisettrici relative agli angoli
•
Baricentro il punto di intersezione delle mediane relative ai lati
Osserva
Un triangolo è equivalente alla metà di un parallelogramma avente la stessa base e la
stessa altezza del triangolo dato.
AB=b
HC=h
A= Area
A=
bxh
2
b=
2xA
h
h=
2xA
b
TRIANGOLI PARTICOLARI
Triangolo equilatero
In un triangolo equilatero l'altezza è la metà del lato per radice di tre.
CH= h
AD=l
h=
l
3
2
da cui si ha: l=
2xh
3
Pertanto in un triangolo equilatero è
sufficiente conoscere il lato o l'altezza
per calcolare l'area e il perimetro. Così,
anche, è sufficiente conoscere l'area per
calcolare il lato o l'altezza.
Triangolo rettangolo avente gli angoli di 30° e 60°
Un triangolo rettangolo avente gli angoli di 30° e 60° è la metà di un triangolo
equilatero. Quindi ha l'ipotenusa il doppio del cateto minore e il cateto maggiore
uguale al cateto minore per la radice di tre.
AB= a (cateto minore)
AC=b (cateto maggiore)
BC=c (ipotenusa)
b=a 3
c=2a da cui si ha: a=
b
3
Pertanto in un triangolo rettangolo avente gli angoli di 30° e 60° è sufficiente conoscere
solo il cateto minore o il cateto maggiore per calcolare l'area e il perimetro. Così, anche, è
sufficiente conoscere l'area per calcolare i lati e il perimetro.
Triangolo rettangolo isoscele
Il triangolo rettangolo isoscele è la metà di un quadrato. In un triangolo rettangolo
isoscele l'altezza relativa all'ipotenusa (CH) è la metà dell'ipotenusa stessa;
l'ipotenusa è 1,41 volte il cateto e il cateto è uguale all'ipotenusa diviso 1,41. Così è
sufficiente conoscere un lato o l'altezza relativa all'ipotenusa per calcolare l'Area o
conoscere l'area per calcolare i lati e l'altezza.
c= Ipotenusa= lato maggiore
a=b= Cateti= lati minori (i cateti sono
congruenti)
h= CH
c= a  2
h=
c
2
da cui si ha
a=
c
2
a= h  2
Triangolo rettangolo
In un triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla
somma dei quadrati costruiti sui cateti.
a= cateto minore
b= cateto maggiore
c= Ipotenusa
a=
 c2 −b2 
b=
 c 2−a 2 
c=
 a 2b 2
QUADRATO
Il quadrato è un rettangolo che ha i lati congruenti.
● Ha le diagonali perpendicolari
l= lato
d= diagonale
A= Area
2p = Perimetro
Se in un quadrato conosci il lato
A= l 2
2p=4l
d=l  2
Se in un quadrato conosci l'Area
l= A
d = 2A
Se in un quadrato conosci la diagonale
A=
d2
2
l=
d
2
ROMBO
Il rombo è un parallelogramma che ha i lati congruenti.
● Ha le diagonali perpendicolari
AB= l ( lato)
BD=d1 (diagonale minore)
AC=d2 (diagonale maggiore)
A= Area (Area)
2p = Perimetro (Perimeter)
DH=h (altezza relativa al lato
Visto che un rombo è equivalente a un rettangolo i cui
lati sono congruenti alle diagonali del rombo stesso
allora:
A=
d1xd2
2
d1=
2A
d2
d2=
2A
d1
Il rombo è anche un parallelogramma che ha come base un lato e di cui DH è l'altezza.
A= lxh
TRAPEZIO
Il trapezio è un quadrilatero avente due lati opposti paralleli.
•
Il trapezio ha gli angoli adiacenti ai lati obliqui supplementari
•
Il trapezio è isoscele se ha i due lati obliqui congruenti
•
Il trapezio isoscele ha le diagonali congruenti, gli angoli a ciascuna base
congruenti, gli angoli opposti supplementari.
•
Il trapezio è rettangolo se ha un lato perpendicolare alle basi
Il trapezio è equivalente ad un triangolo avente la stessa altezza, ma la base uguale alla somma delle
basi del trapezio.
AB= b1 (base maggiore)
DC= b2 (base minore)
DH= h (altezza)
AH e KB proiezioni dei lati obliqui sulla base maggiore
A= b1b2 x
h=
2A
b1b2
b1 =
2A
−b2
h
b2 =
2A
−b1
h
h
2
H